Всем привет! Ко мне часто приходят с вопросами о проблемах в области цифровой обработки сигналов (ЦОС).
Подробно объясняю нюансы и предлагаю необходимые источники информации.
Но, как показало время, всем слушателям не хватает практических задач и примеров в процессе изучения этой области.
В связи с этим я решил написать небольшой интерактивный курс по цифровой обработке сигналов и разместить его на открытый доступ .
Большая часть учебного материала для наглядного и интерактивного представления реализована с использованием Блокнот Юпитера .
Предполагается, что читатель обладает базовыми знаниями высшей математики, а также некоторыми знаниями языка программирования Python. 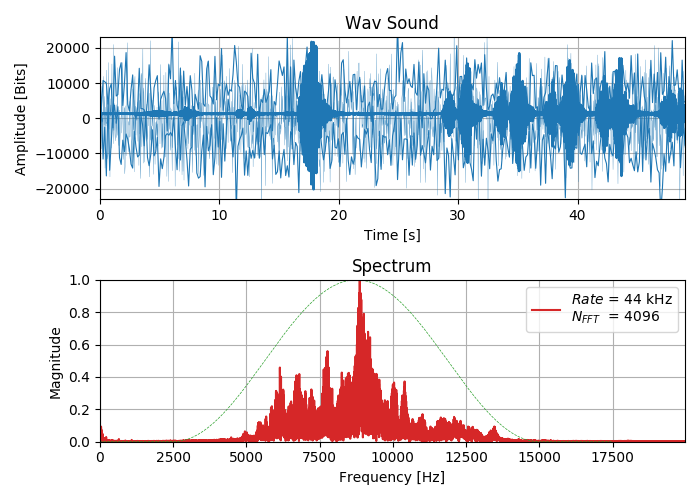
Список лекций
Этот курс содержит материалы в виде полных лекций по различным темам в области цифровой обработки сигналов.Материалы представлены с использованием библиотек Python (пакеты numpy, scipy, matplotlib и др.
).
Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского энергетического института (НИУ МИ).
Часть информации из этих лекций использовалась на обучающих семинарах в г.
Центр современной электроники , где я выступал в качестве лектора.
Кроме того, в данный материал включены переводы различных научных статей, подборка информации из надежных источников и литературы по теме цифровой обработки сигналов, а также официальная документация по пакетам приложений и встроенным функциям библиотек scipy и numpy языка Python. язык.
Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и аналогичны методам из библиотек Python. Все материалы сгруппированы по основным темам цифровой обработки сигналов:
- Сигналы: аналоговые, дискретные, цифровые.
Z-преобразование,
- Преобразование Фурье: амплитудный и фазовый сигнал, ДПФ и БПФ,
- Свертка и корреляция.
Линейная и циклическая свертка.
Быстрый рулон,
- Случайные процессы.
Белый шум.
Функция плотности вероятности,
- Детерминированные сигналы.
Модуляция: AM, FM, FM, чирп.
Манипуляция,
- Фильтрация сигнала: БИХ, КИХ фильтры,
- Оконные функции при фильтрации задач.
Обнаружение слабых сигналов,
- Повторная выборка: прореживание и интерполяция.
CIC-фильтры, фильтры скользящего среднего,
- Непараметрические методы спектрального анализа,
- Усреднение по частоте и времени.
Полифазное БПФ.
Если у меня будет свободное время, я планирую поддерживать и развивать этот проект.
Где найти?
Все материалы - абсолютно бесплатно и доступны в виде открытого репозитория на мой github как проект с открытым исходным кодом .Материалы представлены в двух форматах — в виде Jupyter Notebooks для интерактивной работы, изучения и редактирования и в виде HTML-файлов, составленных из этих блокнотов (после скачивания с GitHub они имеют вполне подходящий формат для чтения и печати).
Ниже приведено очень краткое описание разделов курса с некоторыми пояснениями, терминами и определениями.
Основная информация доступна в оригинальных лекциях, это лишь краткий обзор!
Сигналы.
Z-преобразование Вводный раздел, содержащий основную информацию о типах сигналов.
Введено понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичного скачка).
Все сигналы по способу представления на множестве можно разделить на четыре группы:
- аналоговый – описывается непрерывными во времени функциями,
- дискретный – прерванный во времени с заданным шагом дискретизации,
- квантованные – имеют набор конечных уровней (обычно по амплитуде),
- цифровой – сочетание свойств дискретных и квантованных сигналов.
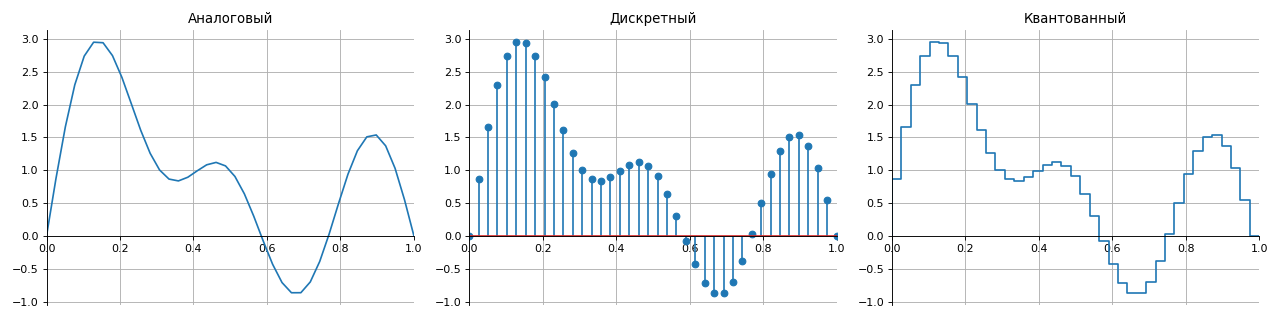
Чтобы правильно восстановить аналоговый сигнал из цифрового без искажений и потерь, используется теорема дискретизации, известная как Теорема Котельникова (Найквиста-Шеннона) .
Любой непрерывный сигнал с ограниченным спектром можно восстановить однозначно и без потерь по его дискретным отсчетам, взятым с частотой, строго превышающей в два раза верхнюю частоту спектра непрерывного сигнала.Такая интерпретация справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты.
Если шаги квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет искажено.
В этом разделе также описывается Z-преобразование и его свойствах показано представление дискретных последовательностей в Z-форме.
Пример конечной дискретной последовательности:
.x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}
Пример той же последовательности в Z-форме:
Х(г) = 2 + г -1 - 2з -2 + 2з -4 + 3з -5 + 1з -6
Преобразование Фурье.
Характеристики.
ДПФ и БПФ В этом разделе описывается концепция временной и частотной области сигнала.
Введено определение дискретного преобразования Фурье (ДПФ).
Рассмотрены прямые и обратные ДПФ и их основные свойства.
Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации частоты и времени).
Отражена эффективность БПФ по сравнению с ДПФ.
В частности, в этом разделе описывается пакет Python scipy.ffpack для вычисления различных преобразований Фурье (синус, косинус, прямое, обратное, многомерное, вещественное).
Преобразование Фурье позволяет представить любую функцию как набор гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и построения цифровых корреляторов, активно применяется в спектральном анализе, применяется при работе с длинными числами.
Особенности спектров дискретных сигналов: 1. Спектральная плотность дискретного сигнала представляет собой периодическую функцию с периодом, равным частоте дискретизации.
2. Если дискретная последовательность настоящий , то модуль спектральной плотности такой последовательности равен даже функция, а аргумент странный функция частоты.
Спектр гармонического сигнала: 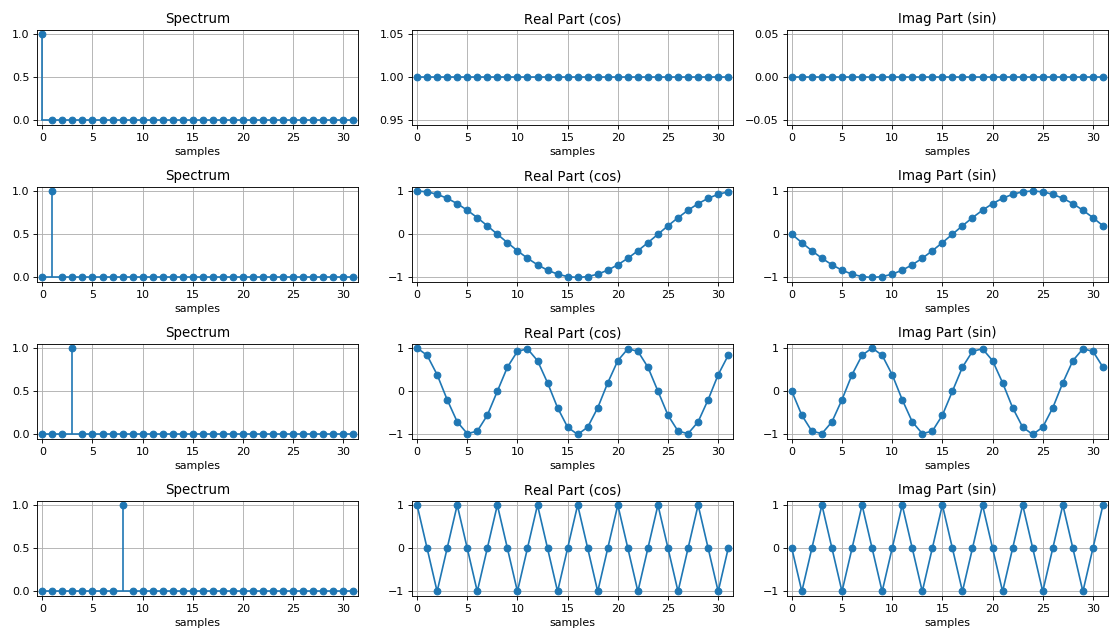
Сравнение эффективности ДПФ и БПФ
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:| Н | ДПФ | БПФ | Соотношение количества сложных дополнений | Отношение количества комплексных умножений | ||
|---|---|---|---|---|---|---|
| Количество операций умножения | Количество операций сложения | Количество операций умножения | Количество операций сложения | |||
| 2 | 4 | 2 | 1 | 2 | 4 | 1 |
| 4 | 16 | 12 | 4 | 8 | 4 | 1.5 |
| 8 | 64 | 56 | 12 | 24 | 5.3 | 2.3 |
| 16 | 256 | 240 | 32 | 64 | 8 | 3.75 |
| 32 | 1024 | 992 | 80 | 160 | 12.8 | 6.2 |
| 64 | 4096 | 4032 | 192 | 384 | 21.3 | 10.5 |
| 128 | 16384 | 16256 | 448 | 896 | 36.6 | 18.1 |
| .
|
.
|
.
|
.
|
.
|
.
|
.
|
| 4096 | 16777216 | 16773120 | 24576 | 49152 | 683 | 341 |
| 8192 | 67108864 | 67100672 | 53248 | 106496 | 1260 | 630 |
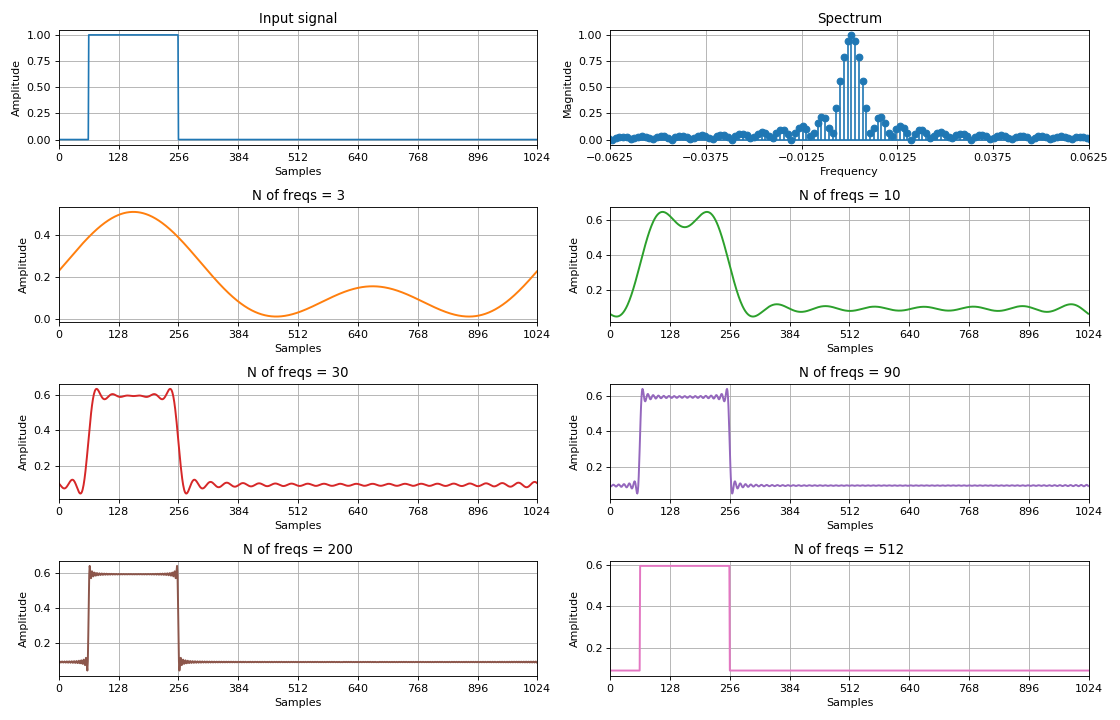
Другими словами, сигнал сложной формы во временной области имеет набор сложных отсчетов в частотной области, которые называются *гармониками*.
Эти показания выражают амплитуду и фазу гармонического воздействия на определенной частоте.
Чем больше набор гармоник в частотной области, тем точнее представляется сложная форма сигнала.
Свертка и корреляция
В этом разделе представлена концепция корреляции и свертки для дискретных случайных и детерминированных последовательностей.Показана связь автокорреляционных и кросс-корреляционных функций со сверткой.
Описаны свойства свертки, в частности рассмотрены методы линейной и циклической свертки дискретного сигнала с детальным анализом на примере дискретной последовательности.
Кроме того, показан метод расчета «быстрой» свертки с использованием алгоритмов БПФ.
В реальных задачах часто возникает вопрос о степени сходства одного процесса с другим или независимости одного процесса от другого.
Другими словами, требуется определить связь между сигналами, то есть найти корреляция .
Корреляционные методы используются в широком круге задач: поиск сигналов, компьютерное зрение и обработка изображений, в радиолокационных задачах для определения характеристик целей и определения расстояния до объекта.
Кроме того, корреляция используется для поиска слабых сигналов в шуме.
Свертка описывает взаимодействие сигналов друг с другом.
Если одним из сигналов является импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть не что иное, как реакция схемы на входное воздействие.
Другими словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Автокорреляционная функция (АКФ) находит применение при кодировании информации.
Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом определяется корреляционными свойствами этой последовательности.
Лучшая кодовая последовательность имеет наименьшую вероятность ложного обнаружения или срабатывания (при обнаружении сигнала, для пороговых устройств) или ложной синхронизации (при передаче и приеме кодовых последовательностей).
В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, рассчитанной по прямой формуле (на основе количества действительных умножений).
Как видите, для длин БПФ до 64 быстрая свертка уступает прямому методу.
Однако по мере увеличения длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает превосходить прямой метод. Очевидно, что чем больше длина БПФ, тем лучше выигрыш частотного метода.
| Н | Свертка | Быстрая свертка | Отношение |
|---|---|---|---|
| 8 | 64 | 448 | 0.14 |
| 16 | 256 | 1088 | 0.24 |
| 32 | 1024 | 2560 | 0.4 |
| 64 | 4096 | 5888 | 0.7 |
| 128 | 16К | 13312 | 1.23 |
| .
|
.
|
.
|
.
|
| 2048 | 4М | 311296 | 13.5 |
Случайные сигналы и шум
В этом разделе представлены понятия случайных сигналов, плотности распределения вероятностей и закона распределения случайной величины.Рассмотрены математические аспекты – среднее (математическое ожидание) и дисперсия (или корень этой величины – стандартное отклонение).
В этом разделе также обсуждается нормальное распределение и связанная с ним концепция.
белый шум , как основного источника шума (помех) при обработке сигнала.
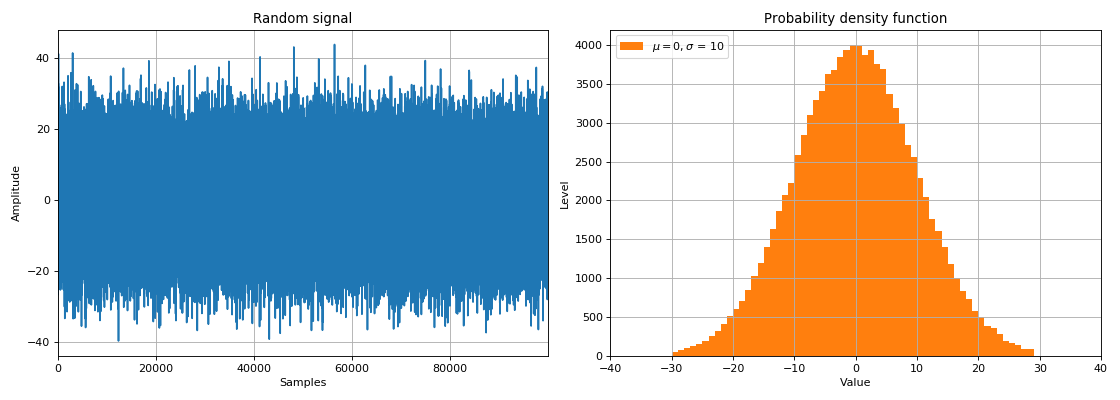
Случайный сигнал — это функция времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторым вероятность .
К основным характеристикам случайных сигналов относятся:
- закон распределения (относительное время пребывания значения сигнала в определенном интервале),
- спектральное распределение мощности сигнала.
В задачах DSP случайные сигналы делятся на два класса:
- шум – случайные колебания, состоящие из набора различных частот и амплитуд,
- сигналы, несущие информацию, обработка которой требует обращения к вероятностным методам.
Когда сигнал проходит через какое-то зашумленное соединение, к сигналу добавляется так называемый белый шум.
Обычно спектральная плотность такого шума равномерно (равномерно) распределена на всех частотах, а значения шума во временной области распределены нормально (закон распределения Гаусса).
Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные моменты времени, он называется аддитивным белым гауссовским шумом (AWGN).
Сигналы, модуляция и манипуляция
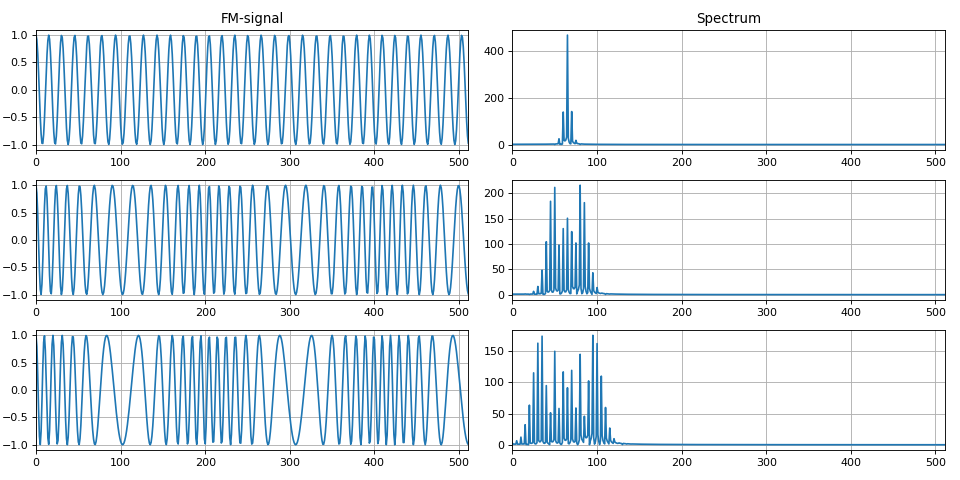
В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала.Введены понятия амплитудной, частотной и фазовой модуляции.
В частности, выделена линейная частотная модуляция, используемая в задачах радиолокации.
Показаны основные характеристики сигналов и спектры модулированных сигналов в зависимости от параметров модуляции.
Для удобства в Python создан набор функций, реализующих перечисленные виды модуляции.
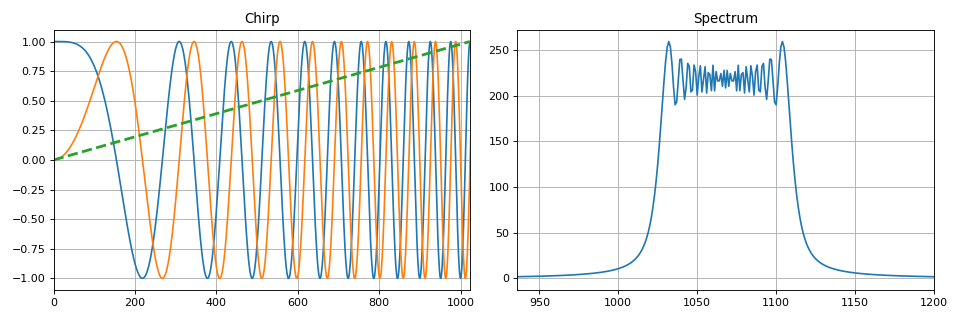
Пример реализации чирп-сигнала: def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
"""
Create Chirp signal
Parameters
----------
amp : float
Signal magnitude
beta : float
Modulation bandwidth: beta < N for complex, beta < 0.5N for real
freq : float or int
Linear frequency of signal
period : integer
Number of points for signal (same as period)
kwargs : bool
Complex signal if is_complex = True
Modulated by half-sine wave if is_modsine = True
"""
is_complex = kwargs.get('is_complex', False)
is_modsine = kwargs.get('is_modsine', False)
t = np.linspace(0, 1, period)
tt = np.pi * (freq * t + beta * t ** 2)
if is_complex is True:
res = amp * (np.cos(tt) + 1j * np.sin(tt))
else:
res = amp * np.cos(tt)
if is_modsine is True:
return res * np.sin(np.pi * t)
return res
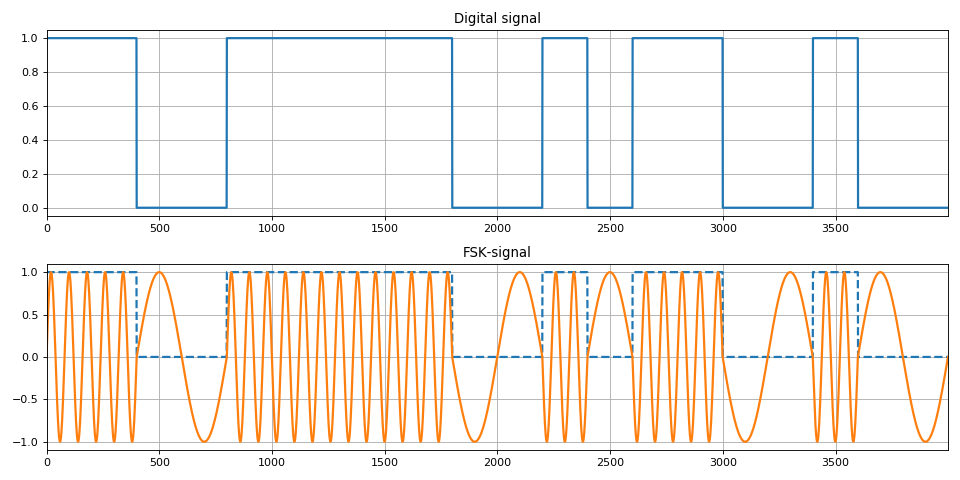
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции – манипуляции.
Как и в случае с аналоговыми сигналами, цифровыми гармоническими структурами можно манипулировать по амплитуде, фазе и частоте (или несколькими способами).
Цифровые фильтры - БИХ и КИХ
Довольно большой раздел посвящен вопросам цифровой фильтрации дискретных последовательностей.В задачах цифровой обработки сигналов данные проходят через схемы, называемые фильтры .
Цифровые фильтры, как и аналоговые, имеют разные характеристики – частотную: АЧХ, Фазовую характеристику, временную: импульсную характеристику, а также передаточную характеристику фильтра.
Цифровые фильтры используются в первую очередь для улучшения качества сигнала — для изоляции сигнала от последовательности данных — или для снижения нежелательных сигналов — для подавления определенных сигналов во входящих последовательностях выборок.
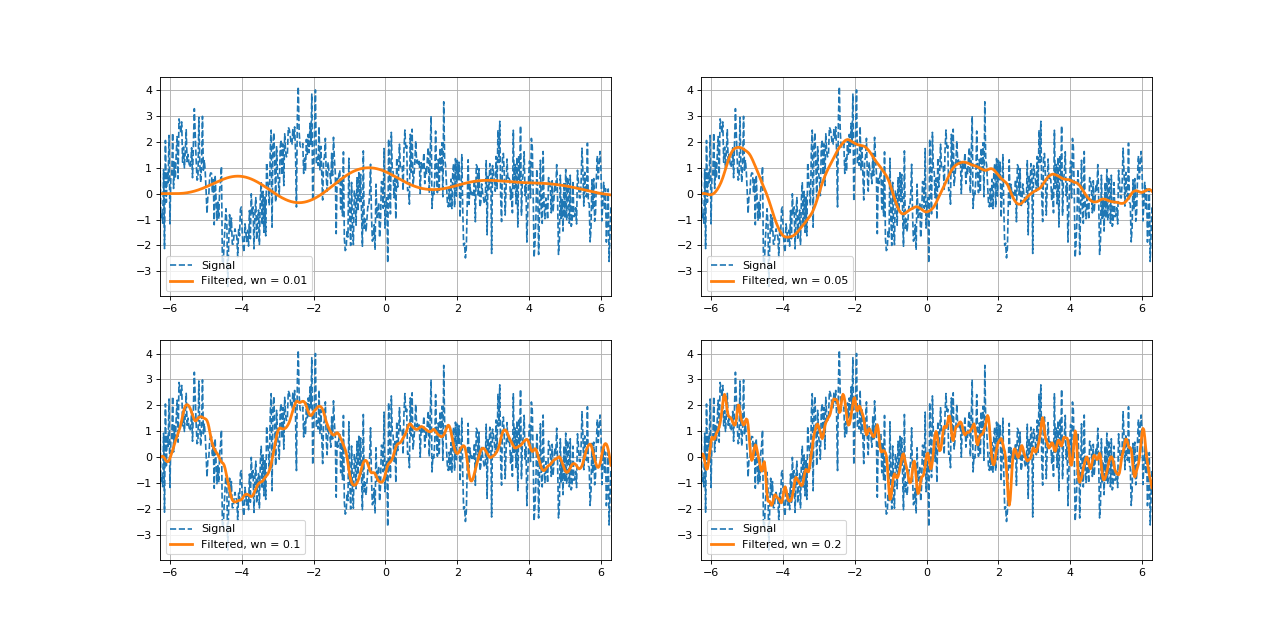
В разделе перечислены основные преимущества и недостатки цифровых фильтров (по сравнению с аналоговыми).
Введено понятие импульсной и передаточной характеристики фильтра.
Рассмотрены два класса фильтров: бесконечная импульсная характеристика (БИХ) и конечная импульсная характеристика (КИХ).
Способ проектирования фильтров по канонический И прямой форма.
Для КИХ-фильтров рассмотрен вопрос о переходе к рекурсивной форме.
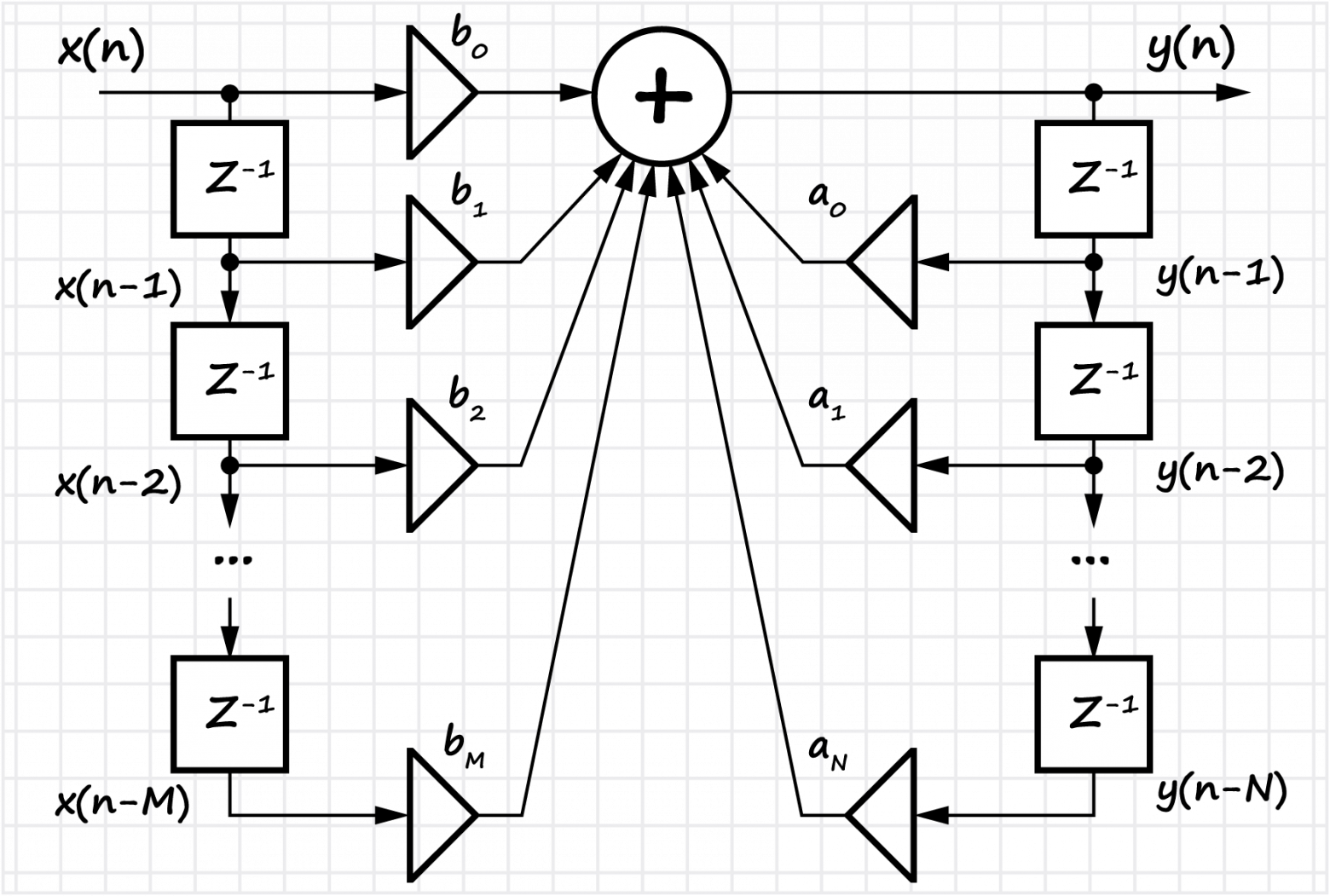
Для КИХ-фильтров показан процесс проектирования фильтра от этапа разработки технического задания (с указанием основных параметров) до программно-аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления чисел, разрядности данных, и т. д.).
Введены определения симметричных КИХ-фильтров, линейной фазовой характеристики и ее связи с понятием групповой задержки.
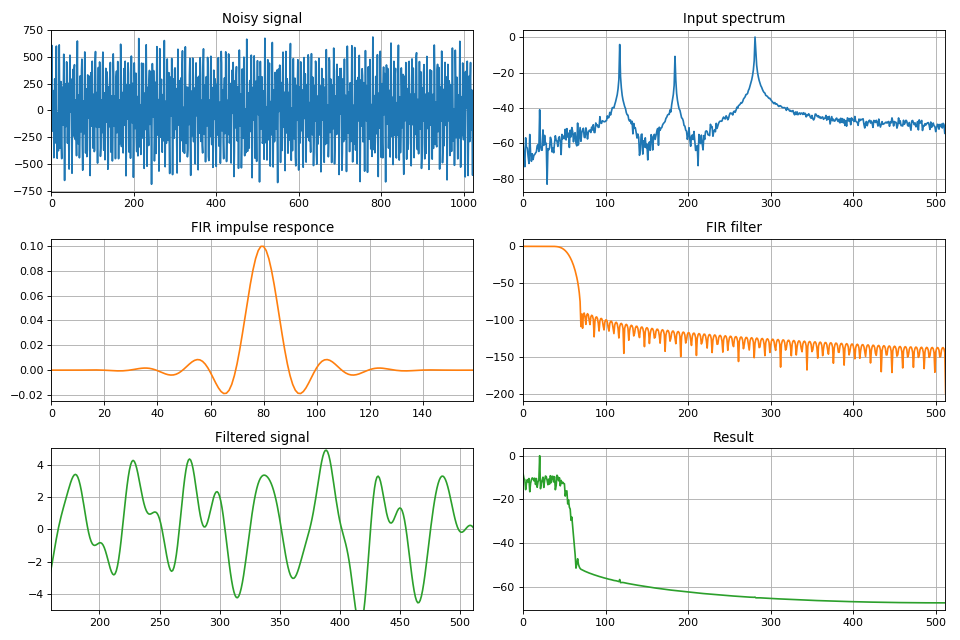
Оконные функции в задачах фильтрации
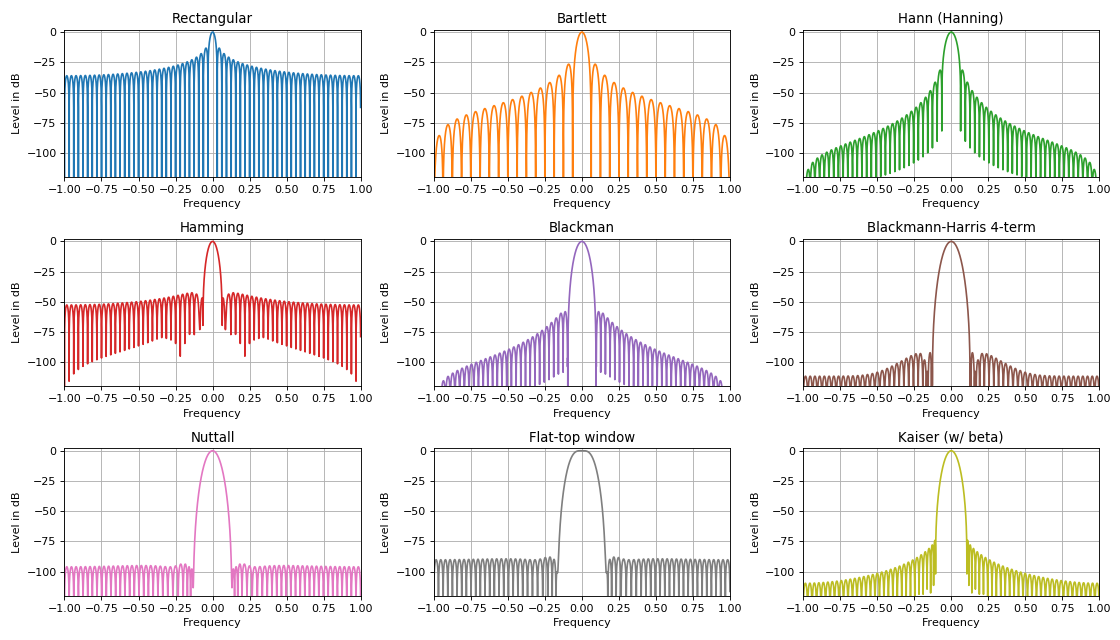
В задачах цифровой обработки сигналов используются оконные функции различной формы, применение которых к сигналу во временной области позволяет качественно улучшить его спектральные характеристики.Большое количество различных окон обусловлено, прежде всего, одной из основных особенностей любого оконного наложения.
Эта особенность выражается в соотношении уровня боковых лепестков и ширины центрального лепестка.
Правило:
Чем сильнее подавление боковых лепестков спектра, тем шире основной лепесток спектра и наоборот.
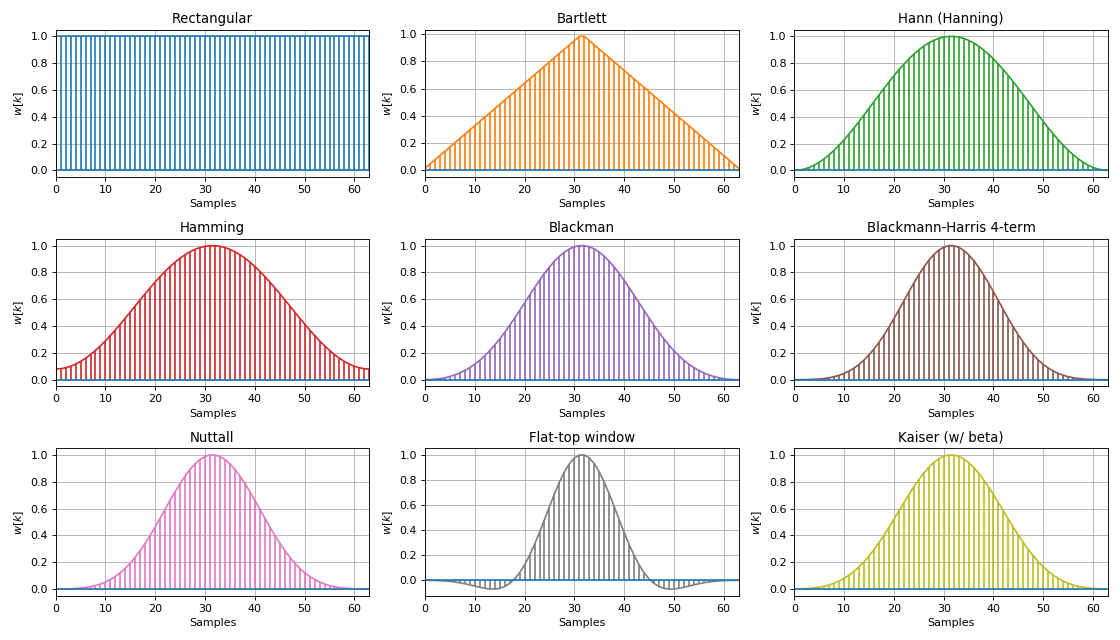
Одним из применений оконных функций является обнаружение слабых сигналов на фоне более сильных путем подавления уровня боковых лепестков.
Основными функциями окна в задачах DSP являются **треугольные, синусоидальные, окна Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, плоская вершина, окна Наттолла, Гаусса, Кайзера** и многие другие.
Большинство из них выражаются через конечный ряд путем суммирования гармонических сигналов с определенными весовыми коэффициентами.
Такие сигналы прекрасно реализуются на практике на любых аппаратных устройствах (программируемых логических схемах или процессорах сигналов).
Ресемплинг.
Децимация и интерполяция В этом разделе рассматриваются вопросы многоскоростной обработки сигналов – изменение частоты дискретизации.
Многоскоростная обработка предполагает, что в процессе линейного преобразования цифровых сигналов можно изменять частоту дискретизации в сторону уменьшения или увеличения либо на дробное число раз.
Это приводит к более эффективной обработке сигналов, поскольку открывает возможность использования минимально допустимых частот дискретизации и, как следствие, существенного снижения требуемой вычислительной производительности проектируемой цифровой системы.
Децимация (децимация) – понижение частоты дискретизации.
Интерполяция – увеличение частоты дискретизации.
В разделе также обсуждается класс однородных КИХ-фильтров, которые называются интегральными гребенчатыми фильтрами (CIC, Cascaded integrator-comb).
Показаны реализация, основные свойства и особенности CIC-фильтров.
Благодаря линейности математических операций, происходящих в CIC-фильтре, возможно каскадное подключение нескольких фильтров подряд, что дает пропорциональное снижение уровня боковых лепестков, но и увеличивает «развал» основного лепестка.
амплитудно-частотной характеристики.
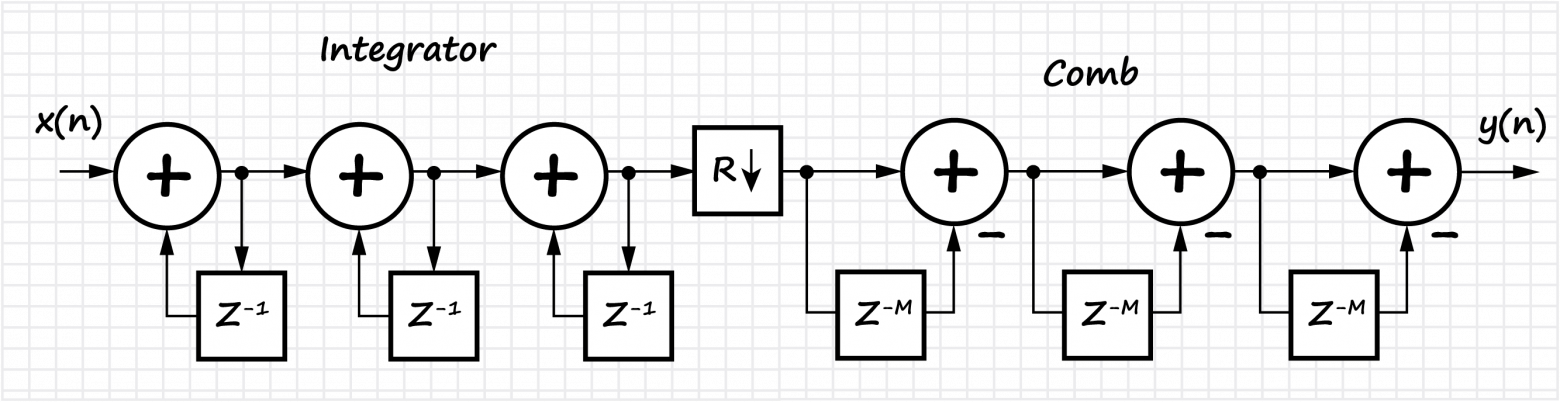
График АЧХ фильтра в зависимости от коэффициента децимации: 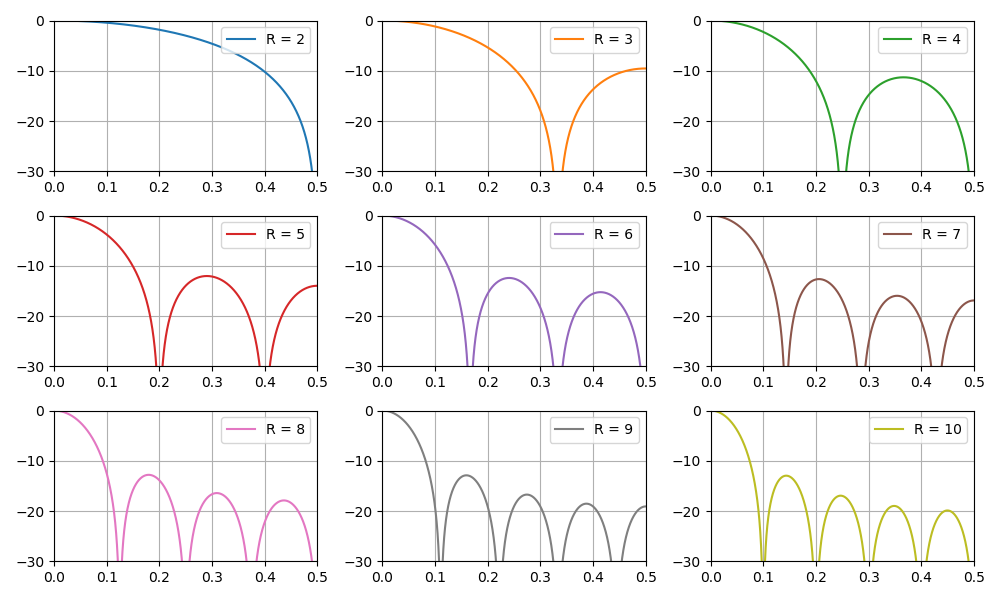
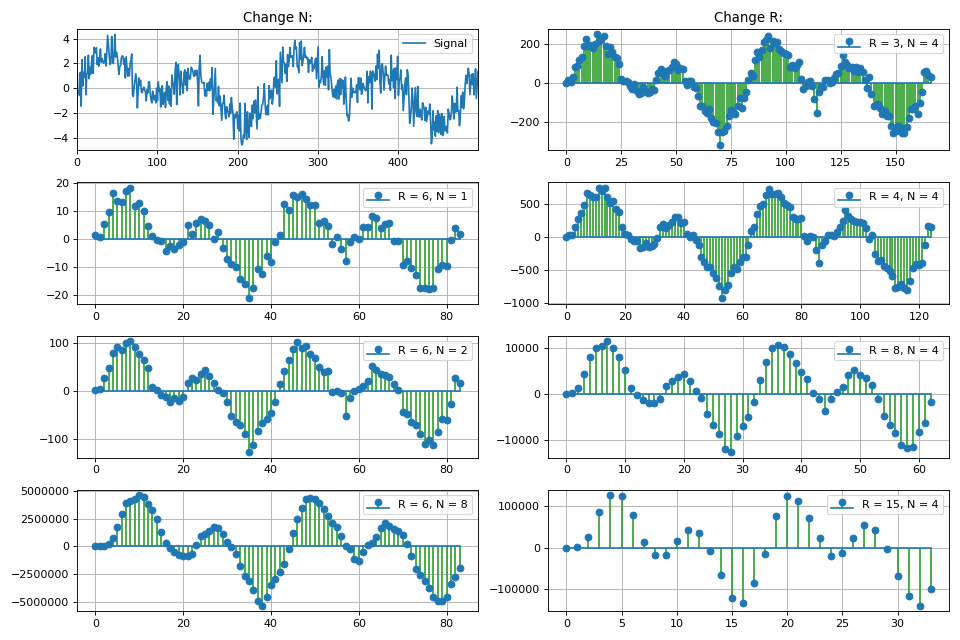
В этом разделе также рассматривается вопрос увеличения разрядности данных на выходе CIC-фильтра в зависимости от его параметров.
Особенно это важно в задачах реализации программного обеспечения, в частности на ПЛИС.
Для практической реализации CIC-фильтров на Python разработан отдельный класс.
CicFilter , который реализует методы прореживания и интерполяции.
Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из пакета scipy Python. Класс Python CicFilter для цифровой обработки сигналов
class CicFilter:
"""
Cascaded Integrator-Comb (CIC) filter is an optimized class of
finite impulse response (FIR) filter.
CIC filter combines an interpolator or decimator, so it has some
parameters:
R - decimation or interpolation ratio,
N - number of stages in filter (or filter order)
M - number of samples per stage (1 or 2)*
* for this realisation of CIC filter just leave M = 1.
CIC filter is used in multi-rate processing. In hardware
applications CIC filter doesn't need multipliers, just only
adders / subtractors and delay lines.
Equation for 1st order CIC filter:
y[n] = x[n] - x[n-RM] + y[n-1].
Parameters
----------
x : np.array
input signal
"""
def __init__(self, x):
self.x = x
def decimator(self, r, n):
"""
CIC decimator: Integrator + Decimator + Comb
Parameters
----------
r : int
decimation rate
n : int
filter order
"""
# integrator
y = self.x[:]
for i in range(n):
y = np.cumsum(y)
# decimator
y = y[::r]
# comb stage
return np.diff(y, n=n, prepend=np.zeros(n))
def interpolator(self, r, n, mode=False):
"""
CIC inteprolator: Comb + Decimator + Integrator
Parameters
----------
r : int
interpolation rate
n : int
filter order
mode : bool
False - zero padding, True - value padding.
"""
# comb stage
y = np.diff(self.x, n=n,
prepend=np.zeros(n), append=np.zeros(n))
# interpolation
if mode:
y = np.repeat(y, r)
else:
y = np.array([i if j == 0 else 0 for i in y for j in range(r)])
# integrator
for i in range(n):
y = np.cumsum(y)
if mode:
return y[1:1 - n * r]
else:
return y[r - 1:-n * r + r - 1]
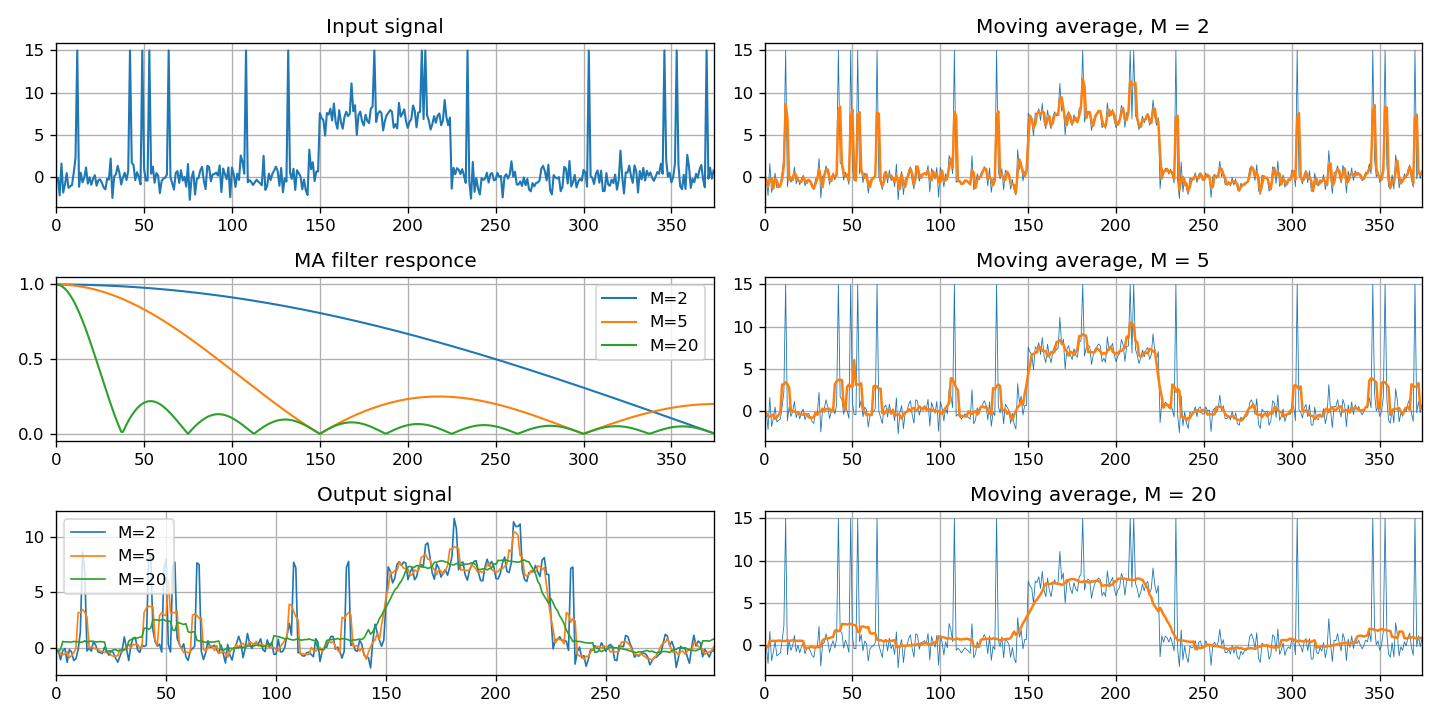
Наконец, в этом разделе представлен особый класс фильтров — скользящее среднее.
Показаны три метода реализации: посредством свертки сигнала, с использованием КИХ-фильтра и БИХ-фильтра.
Заключение
Надеюсь, этот курс лекций вместе с моими предыдущими статьями о цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов.Этот проект будет совершенствоваться и дополняться новым полезным и не менее интересным материалом.
Следите за развитием! Помимо этого материала я поддерживаю и развиваю ваш проект на основных модулях ЦСП (на Python).
Он содержит пакет для генерации различных сигналов, класс CIC-фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм расчета сверхдлинного БПФ с использованием двумерного методы преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).
UPD: 20.04.2020
В курс добавлены две лекции:- Непараметрические методы спектрального анализа ( Владимир Фадеев )
- Усреднение по частоте и времени.
Полифазное БПФ.

-
Умный Дом На .Net — Выпуск Thinkinghome 3.0
19 Oct, 24 -
Что Такое Итсм?
19 Oct, 24 -
Форматы Dvd+R И Dvd+Rw Официально Признаны.
19 Oct, 24


