Кубок России Code - По Итогам Отборочного Тура

Отборочный тур состоялся 14 мая.

Кубок России по Кодексу 2017 .

По традиции мы публикуем анализ задач и подводим итоги.

А.

Маленькие числа Б.

Новая клавиатура С.

Складывание фигуры Д.

Острые треугольники ?.

Объединение массивов Ф.

Два поддерева В туре приняли участие 603 человека: примерно по 200 лучших программистов из каждого отборочного тура.

По итогам отборочного тура мы вывели в финал 55 участников.

Ни один участник в отборочном туре не смог решить все шесть задач.

15 человек выполнили пять заданий.

Помимо четырёх, есть ещё 55 участников.

Тройка лучших:

1. На первом месте, со значительным отрывом от преследователей (на 15 минут), оказался Михаил Ипатов из Костромы.

2. Второе место занял Михаил Тихомиров из Москвы.

3. На третьем месте Игорь Пышкин из Санкт-Петербурга.

1. Митричев Петр, Цюрих, Швейцария
2. Геннадий Короткевич, Санкт-Петербург, Россия
3. Александр Останин, Долгопрудный, Россия
4. Ершов Станислав, Санкт-Петербург, Россия
5. Джокич Никола
6. Данилюк Алексей, Одинцово, Россия
7. Ду Юхао, Пекин, Китай

Поздравляем всех, кто прошел в финал, который состоится в сентябре 2017 года.

Ну а теперь – разбор заданий.

А.

Небольшое количество

Недавно его учили в школе делить и умножать, и он сразу побежал делить и умножать свои любимые числа.

Сначала он записал цифры в свой блокнот. а И б , после чего он решил, что последовательно выполнит с ними одну из трёх операций:

• Разделите оба числа на один из их общих делителей;
• Делиться а на один из его делителей г , А б умножить на г ;
• Делиться б на один из его делителей г , А а умножить на г .

Поскольку Влад еще маленький, ему нравятся числа поменьше, поэтому он стремится минимизировать сумму записанных в тетрадке цифр.

Он не может справиться сам.

Помогите Владу определить, какую минимальную сумму чисел можно получить такими операциями, и приведите пример пары чисел, которые можно получить в результате.

Формат ввода Входные данные содержат несколько тестовых примеров.

В первой строке указывается количество тестов т (1 ≤  т  ≤ 500).

Каждый тест описывается следующим образом: одна строка описания теста содержит два числа.

а И б (1 ≤  а ,  б  ≤ 10 ⁹ ) — любимые числа Влада.

Выходной формат Для каждого теста в отдельной строке выведите ответ на него — пару с минимальной суммой, которую можно получить, применив действия из условия.

Если ответов несколько, то разрешено вывести любой из них.

Примеры Входные данные 2 4 5 4 6 Выход 1 5 2 3 Анализ проблемы Для начала давайте разберем цифры а И б до простых.

Теперь заметим, что если какое-то простое число п включен в работу аб в степень большую, чем первое, то мы можем либо сразу разделить оба числа на число п , или если одно из чисел не делится на п , затем переносим в него множитель п из другого числа, затем разделите на п .

Очевидно, что четность вхождений простых чисел в произведение аб не меняется во всех операциях.

Тогда давайте оставим все простые числа в первой степени.

Осталось цифр п ₁ ,  п ₂ , .

,  п _н .

Назовем произведение всех этих простых чисел д , д  ≤  аб .

Утверждается, что таких простых чисел не может быть более 14. Если 1 ≤ а ,  б  ≤ 10 ⁹ , то произведение аб  ≤ 10 ¹⁸ , а произведение первых 15 простых чисел превышает 10 ¹⁸ ).

Теперь обратите внимание, что окончательный ответ — это пара чисел ( Икс ,  й ) такой, что ху  =  д .

Отсюда следует, что второй элемент пары определяется однозначно по первому.

Давайте пройдемся по всем возможным делителям д цифры Икс позади О (2 ^н ), и выберите лучшую пару.

Б.

Новая клавиатура

Она поддерживает н раскладки В каждой раскладке можно набирать определенный подмножество строчных букв латинского алфавита.

Пронумеруем макеты от 1 до н .

Петя хочет набрать какое-то сообщение, состоящее из м строчные буквы латинского алфавита.

Первый макет изначально активен.

Петя может выполнять следующие действия:

• Переключить раскладку.

  Затем, если текущий макет имел номер я , новый макет будет иметь номер я мод н + 1, где mod — операция взятия остатка по модулю.

  Если предыдущее действие Пети также переключило раскладку, то это действие будет выполнено б миллисекунды, иначе это действие займет а миллисекунды

• Наберите символ.

  Петя может добавить в конец текущего сообщения любую букву, содержащуюся в текущей раскладке.

  Он потратит на это действие с миллисекунды

Раскладка, остающаяся включенной после набора сообщения, может быть любой.

Формат ввода Первая строка содержит четыре целых числа н , а , б И с — количество раскладок клавиатуры и количество миллисекунд, необходимое для переключения раскладки и ввода символа (1 ≤ н  ≤ 2 000, 1 ≤  б  ≤  а  ≤ 10 ⁹ , 1 ≤  с  ≤ 10 ⁹ ).

В следующих н В строках содержится описание раскладок.

Каждая раскладка описывается непустой строкой, в которой каждая строчная буква латинского алфавита встречается не более одного раза — подмножество букв, которые можно набрать в данной раскладке.

Буквы в этой строке расположены в алфавитном порядке.

Последняя строка содержит строку с — сообщение, которое Петя хочет набрать (длина строки с от 1 до 2000).

Строка s состоит из строчных латинских букв.

Выходной формат Выведите одно целое число — минимальное количество миллисекунд, необходимое для набора сообщения.

Выведите  - 1, если сообщение невозможно напечатать.

Примеры Входные данные 5 3 2 1 абв д е ж защита abcdef Выход 15 Входные данные 1 1 1 1 а я Выход -1 Анализ проблемы Для решения используем метод динамического программирования.

Состояние — d[i][j][k], где я — флаг, указывающий тип предыдущего действия (0, если это переключение раскладки, и 1, если это набор символа), дж — номер текущего макета и к — количество набранных символов.

Значение представляет собой минимальное время, необходимое для достижения этого состояния.

Давайте перейдем к .

Для фиксированного к давай разберемся дж от 1 до н дважды.

Обновление d[0][j % n + 1][k] = min(d[0][j % n + 1][k], min(d[0][j][k] + b, d[ 1][j][k] + а)).

Сортировать по дж от 1 до н вам это нужно дважды, потому что после ввода к го символа может быть включена раскладка с номером большим, чем раскладка, в которой будет набран следующий символ, и придется переключать раскладки в цикле до нужной.

После этого мы разберемся дж еще раз и обновите значения для к + 1. Если в дж -й макет к символ сообщения, d[1][j][k + 1] = min(d[0][j][k], d[1][j][k]) + c. В конце ответ min(d[1][j][m]), где м = длина(ы) , всем дж от 1 до н .

C. Складывание фигурки

Когда ему это надоело, он заметил, что создал стройную клетчатую фигуру из к ячейки - между любыми двумя заштрихованными клетками существует путь по другим заштрихованным клеткам, причем соседние клетки на этом пути имеют общую сторону.

Аккуратно вырезав ее из тетради, он сложил ее пополам по клеточной линии сетки (по горизонтали или вертикали - точно не запомнил), а также нарисовал в тетради копию сложенной фигуры.

И не зря! Петя потерял фигурку, и у него осталась только копия сложенной фигурки, нарисованная в блокноте.

Теперь он хочет восстановить первоначальную фигуру.

Не всегда удается однозначно восстановить первоначальную фигуру, но Петя решил, что ему будет достаточно нарисовать хоть какую-нибудь фигуру из к клеточки, которые можно сложить пополам так, чтобы получилась сложенная фигурка у него.

Помогите ему - найдите любую оригинальную связную фигурку из к клетки, удовлетворяющие этому условию.

Давайте рассмотрим второй тестовый пример из условия.

В нем сложенная фигура представляет собой букву «П», а исходная фигура состоит из 12 клеток.

Один из возможных вариантов исходной фигуры представлен на рисунке (сгиб происходит по прямой линии).

й  = 3):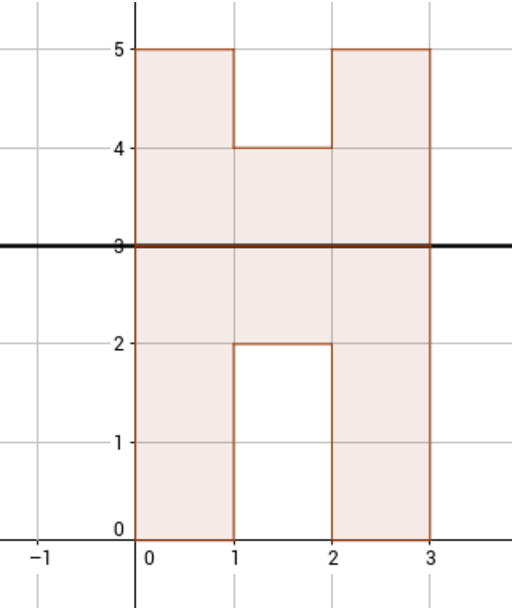



Формат ввода Входные данные содержат несколько тестовых примеров.

В первой строке указывается количество тестов т (1 ≤  т  ≤ 200).

Каждое из следующих т тесты описываются следующим образом: первая строка описания теста содержит два целых числа н , к — количество заштрихованных клеток, составляющих сложенную фигуру Васи, и количество клеток в исходной фигуре (1 ≤ н < к  ≤ 10 ⁵ ).

В каждом из следующих н строки содержат два числа Икс _я , й _я — координаты нижнего левого угла я ячейка цвета ( - 10 ⁸  ≤  Икс _я ,  й _я  ≤ 10 ⁸ ).

Гарантируется, что все заштрихованные клетки различны и образуют связную фигуру.

Гарантируется, что сумма к во всех тестах одних входных данных не превышает 10 ⁵ .

Выходной формат Для каждого теста выведите ответ на него.

Вам нужно распечатать описание фигуры и способы ее согиба, чтобы получить форму из входного файла.

В первой строке выведите линию сгиба, а в к следующие строки содержат два целых числа ( Икс' _я ,  да' _я ) — координаты ячеек связной фигуры, которую можно сложить пополам по нарисованной линии сгиба, чтобы получить фигуру во входных данных.

Линию сгиба необходимо провести одним из 4 способов:

• л число - изгиб выполнен по прямой линии х = число левая часть накладывается поверх правой;
• р число - изгиб выполнен по прямой линии х = число , правая часть накладывается поверх левой;
• ты число - изгиб выполнен по прямой линии y = число , верхняя часть накладывается поверх нижней;
• Д число - изгиб выполнен по прямой линии y = число , нижняя часть накладывается поверх верхней.

Гарантируется, что такая фигура существует. Если совпадающих ответов несколько, вы можете распечатать любой из них.

Примеры Входные данные 2 7 14 0 0 0 1 0 2 1 2 2 2 2 1 2 0 7 12 0 0 0 1 0 2 1 2 2 2 2 1 2 0 Выход Л 0 0 0 0 1 0 2 1 2 2 0 2 1 2 2 -1 0 -1 1 -1 2 -2 2 -3 2 -3 1 -3 0 У 3 0 0 0 1 0 2 1 2 2 2 2 1 2 0 0 3 1 3 2 3 0 4 2 4 Анализ проблемы Обратите внимание, что возможных линий сгиба ровно четыре: две по горизонтали и две по вертикали, так как фигура должна полностью лежать на одной стороне сгиба и также касаться его.

Возьмем любую из ячеек сложенной фигуры с минимальной координатой по оси ОХ — ячейку ( Икс _я ,  й _я ).

В качестве линии сгиба возьмите вертикальную прямую линию.

Икс  =  Икс _я касаясь этой клетки.

Теперь левую нужно восстанавливать к – n ячеек исходной фигуры так, чтобы после наложения левой части по линии сгиба на правую из входных данных получилась сложенная фигура.

Потому что к  –  н  ≤  н (иначе после изгиба их было бы больше н ячеек), достаточно изолировать от сложенной фигуры к – n ячейки, образующие связную фигуру, содержащую ячейку ( Икс _я ,  й _я ).

Это можно сделать с помощью простого обхода в глубину.

D. Острые треугольники

Таня решила посоревноваться с Дмитрием.

Конечно, она планирует использовать компьютер.

Сначала она хочет решить следующую проблему.

Данный н точек на плоскости, нужно найти количество остроугольных треугольников с вершинами в этих точках.

Треугольник называется остроугольным, если все его углы строго меньше 90 градусов.

Формат ввода Входные данные содержат несколько тестовых примеров.

В первой строке указывается количество тестов т (1 ≤  т  ≤ 666).

Каждый из тестов описывается следующим образом: первая строка описания теста содержит номер н (3 ≤  н ≤ 2000) — количество баллов.

Следующие n строк содержат по два числа каждая.

Икс _я , й _я ( - 10 ⁹  ≤  Икс ,  й  ≤ 10 ⁹ ) — координаты точек.

Гарантируется, что все баллы в одном тесте различны.

Суммарное количество баллов по всем тестам одних входных данных не превышает 2000. Выходной формат Для каждого теста на отдельной строке выведите ответ на него — количество остроугольных треугольников с вершинами в данных точках.

Примеры Входные данные 2 5 1 1 2 2 3 3 4 1 6 4 5 0 0 3 1 5 1 5 -1 1 3 Выход 3 4 Анализ проблемы Чтобы посчитать остроугольные треугольники, достаточно из общего числа треугольников вычесть количество прямоугольных и тупоугольных треугольников.

Будем считать три точки на одной прямой вырожденным тупоугольным треугольником.

Общее количество треугольников, которые можно построить с вершинами в данных точках, равно С _н ³ .

Примечание: количество прямоугольных и тупоугольных треугольников равно числу прямых и тупых углов с вершинами в данных точках.

Осталось посчитать количество углов не менее 90 градусов с вершинами в данных точках.

Пройдемся по угловой точке и отсортируем все остальные точки по углу относительно этой.

Давайте воспользуемся методом двух указателей.

Давайте посмотрим на вторую точку, которая будет образовывать угол.

Для расчета количества подходящих третьих точек достаточно заметить, что все точки, образующие с двумя другими точками угол не менее 90 градусов, лежат на отрезке в отсортированном порядке и что отрезок смещается только в сторону увеличения угла.

.

Время выполнения решения: На ² журнал (п)) .

E. Объединение массивов

,  а _н ] И Б  = [ б ₁ ,  б ₂ , .

,  б _м ].

Давайте позвоним им к -слияние лексикографически минимального массива чисел р длина к , который разбивается на две непустые подпоследовательности, первая из которых является подпоследовательностью массива А , а вторая является подпоследовательностью массива Б .

Формально говоря, нам нужно найти лексикографически минимальный массив р  = [ р ₁ ,  р ₂ , .

,  р _к ], для которых существуют непустые наборы индексов 1 ≤ я _1, 1 < я _1, 2 < .

 < я _{1,  т}  ≤  н и 1 < дж _1, 1 < дж _1, 2 < .

 < дж _{1,  к  -  т}  ≤  м в исходных массивах, а также наборах индексов 1 ≤ я _2, 1 < я _2, 2 < .

 < я _{2,  т}  ≤  к и 1 ≤ дж _2, 1 < дж _2, 1 < .

 < дж _{2,  к  -  т}  ≤  к , такой, что:

• Для любого 1 ≤ п  ≤  т , 1 ≤  д  ≤  к  -  т сделанный я _{2,  п}  ≠  дж _{2,  д} ;
• Для любого 1 ≤ п  ≤  т сделанный а _{я 1,  п}  = р _{я 1,  п} ;
• Для любого 1 ≤ п  ≤  к -  т сделанный б _{дж 1,  п} =  р _{дж 1,  п} .

На основе двух заданных массивов А И Б , а также число к Найди их к -Союз р .

Формат ввода Первая строка ввода содержит число н - размер массива А (1 ≤  н  ≤ 3000).

Вторая строка содержит н цифры а _я - множество А (1 ≤  а _я  ≤ 3000).

В третьей строке записано число м - размер массива Б (1 ≤  м  ≤ 3000).

Четвертая строка содержит м цифры б _я - множество Б (1 ≤  б _я  ≤ 3000).

В последней строке записано число к (2 ≤  к  ≤  н  +  м ).

Выходной формат Выход к -комбинация массивов, указанных во входном файле.

Примеры Входные данные 7 1 2 1 3 1 2 1 4 1 2 3 1 9 Выход 1 1 1 1 2 1 2 3 1 Анализ проблемы Мы предлагаем два решения этой проблемы: Хорошо ² • журнал (к)) И Хорошо ² ) .

Решение для Хорошо ² • журнал (к)) Разобьем решение проблемы на три пункта:

1. Для каждого массива Икс ( А или Б ) и каждая длина 1 ≤ длина ≤ |X| мы найдем minSubsequenceX[длина] — лексикографически минимальная подпоследовательность X длины length.
2. Пройдемся по длине подпоследовательности в первом массиве — 1 ≤ т  ≤  мин ( к – 1, |A|).

   Если 1 ≤ к  –  т ≤ |B|, возьмем минподпоследовательность _А [т] И минподпоследовательность _Б [к – т] , их нужно объединить.

3. Объединим две подпоследовательности в одну, получив тем самым лексикографически минимальную подпоследовательность длины к , мы обновим ответ.

• Давайте сделаем математику следующий[я][с] , который будет хранить следующее после я появление персонажа с В Икс .

• Давайте сделаем математику первыйсимвол[длина][я] — первый символ лексикографически минимальной подпоследовательности массива Икс [ я .

  | Икс | – 1] длина длина .

  Для этого обратите внимание на следующее:

  • Если дж ₁ = следующий[i][1] существует, то первыйсимвол[1][i] , первыйсимвол[2][я] ,… первыйсимвол[|X| – j ₁ ][я] начать с 1;
  • Если дж ₂ = следующий[i][2] существует, то первыйсимвол[|X| – j ₁ + 1][я] , .

    , firstSymbol[|X| – j ₂ ][i] начать с 2;

  • .

  • Если дж _{|алфавит|} = следующий[i][|алфавит| существует, то firstSymbol[max(|X| – j ₁ , |X| – j ₂ , .

    , |X| – j _{|алфавит| - 1} ) + 1][i], .

    , firstSymbol[|X| – j _{|алфавит|} ][я] начать с |алфавит| .

    Где алфавит — максимально возможное число в массиве Икс .

• Посчитав первыйсимвол[длина][я] , мы можем восстановить лексикографически минимальную подпоследовательность Икс для каждой длины итеративно по одной букве за раз.

Нахождение двух лексикографически минимальных подпоследовательностей С _А И С _Б , их необходимо объединить в одну лексикографически минимальную длину к .

Мы будем перемещаться по подпоследовательностям с помощью двух указателей п ₁ И п ₂ .

Если С _{Ап 1}  ≠  С _{Бп 2} , затем переместите указатель на меньшее число.

Если С _{Ап 1}  =  С _{Бп 2} , используйте двоичный поиск, чтобы найти самый большой общий префикс С _А [п _1. |С _А |] И С _Б [п _2. |С _Б |] и сравните следующие числа.

Чтобы сравнить подсегменты С _А И С _Б вы можете использовать хеши.

Этот предмет работает для О((|S _А | + |С _Б |)•log(max(|S _А |, |С _Б |))) = O(k•log(k)) .

В сумме, суммируя все три пункта, получаем асимптотику О(|А| ² + |Б| ² + к ² •log(k)) = O(k ² • журнал (к)) .

Решение для Хорошо ² ) Давайте назовем массив А ноль, а массив Б - первый.

Мы будем строить ответ по одному элементу за раз.

Мы также будем поддерживать вспомогательное значение дп[я][j] , Где я — номер массива (0 или 1), и дж — индекс в этом массиве.

дп[я][j] равен минимальному индексу в массиве 1 - я , из которого можно продолжить построение ответа, если в массиве я мы сосредоточимся на индексе дж .

На т й из к итераций построения ответа найдем минимальный элемент такой, что, добавив его к ответу, последовательность можно будет завершить, т. е.

чтобы оставшиеся элементы были не менее к  –  т – 1.Также нужно учитывать, что обе подпоследовательности обоих массивов, из которых строится ответ, должны быть непустыми.

После добавления найденного элемента в в ответ на О(|А| + |B|) обновить значения дп .

Для этого воспользуемся массивом, рассчитанным в предыдущем решении следующий .

F. Два поддерева

Рассмотрим вершину в , который имеет хотя бы одну вершину в поддереве на расстоянии к от в .

Мы позвоним к -вершинное поддерево в дерево, полученное из поддерева узла в удаление всех вершин, расстояние от которых до в более к .

Например, на рисунке ниже 2-поддерево узла 3 отмечено красным.

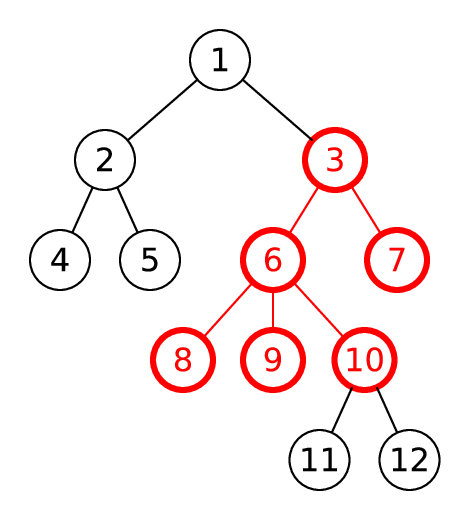
Два дерева будем называть одинаковыми, если можно перенумеровать вершины первого так, чтобы получить второе, при этом изменение порядка потомков в вершинах не допускается.

Например, следующие два дерева не совпадают: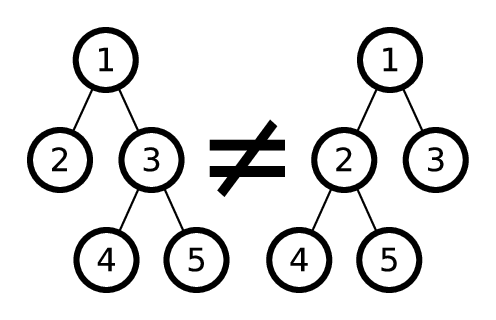



Дано висящее дерево.

Требуется определить наибольшую к так, что у него есть два одинаковых к - поддеревья, корни которых различны.

Эти поддеревья могут пересекаться.

На рисунке показаны примеры деревьев.

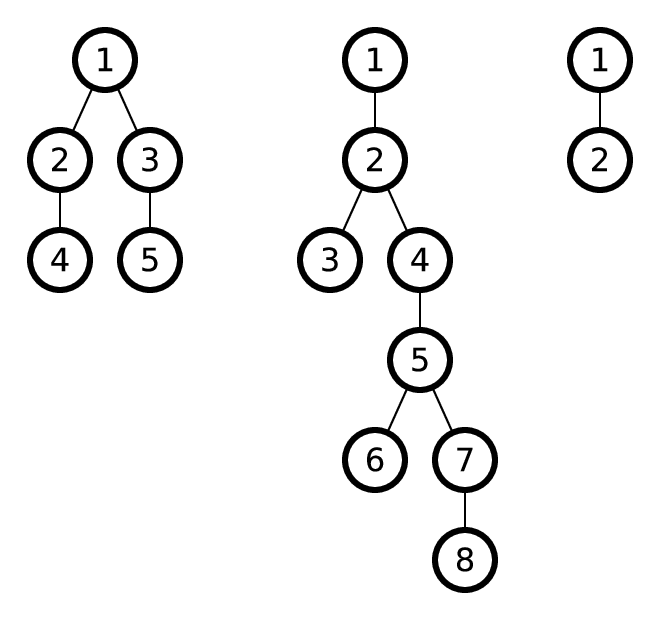
В первом примере корнями одинаковых 1-поддеревьев являются вершины 2 и 3. Во втором примере корнями одинаковых 3-поддеревьев являются вершины 1 и 4. В третьем примере корнями одинаковых 0-поддеревьев являются вершины 1 и 2. Формат ввода В первой строке записано число т — количество тестов (1 ≤ т  ≤ 10 ⁴ ).

Каждый из т тестов описывается следующим образом: первая строка содержит номер н — количество вершин (2 ≤ н  ≤ 10 ⁵ ).

С последующим н линии.

В я дан номер CNT _я — количество детей вершины я , а затем следуйте CNT _я Numbers - номера детей вершин я .

Вершины нумеруются начиная с единицы.

Корнем дерева является вершина 1. Гарантируется, что данный граф является деревом с корнем в 1. Сумма н для всех тестов в одних входных данных не превышает 2 10 ⁵ .

Выходной формат Для каждого теста в отдельной строке выведите максимальное к такие, что есть два одинаковых к - поддеревья с разными корнями.

Примеры Входные данные 3 5 2 2 3 1 4 1 5 0 0 8 1 2 2 3 4 0 1 5 2 6 7 0 1 8 0 2 1 2 0 Выход 1 3 0 Анализ проблемы По условию в к -поддерево должно иметь вершины на глубине к .

Мы временно удалим это требование.

Давайте рассмотрим все к -поддеревья для некоторых к .

Их можно разделить на классы эквивалентности.

Назначим каждой вершине с _к [в] — метка класса эквивалентности, к которому он принадлежит к -под деревом.

В к = 0 все с ₀ [в] равны, поскольку 0-поддерево любой вершины является само собой.

В к  = 1 с ₁ [в] равно числу детей вершины.

Давайте учиться на массивах с _к [в] И с _м [в] построить массив с _к + м [в] .

Сначала назначим каждую вершину в множество обр.

_к + м [в] , который будет однозначно определять класс эквивалентности своего к + м - поддерево.

Позволять ты ₁ , .

,  ты _с - потомки пика в на расстоянии к приказ обойти ДФС .

Тогда давайте сопоставим вершину в множество обр.

_к + м [v] = c _к [в], с _м [ты ₁ ], .

, c _м [ты _с ] .

То есть к + м — указано поддерево вершины к -поддерево вершины и м -поддеревья нижней части к -поддерево.

Ниже представлена иллюстрация к к = 3 и м  = 1.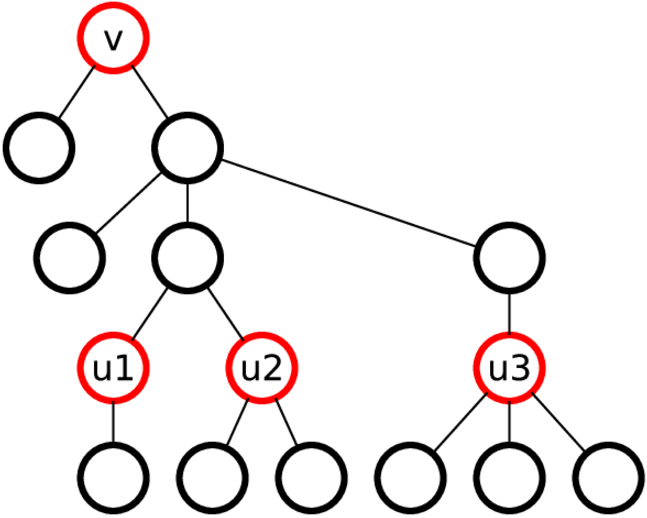



Получить для каждой вершины список ее потомков на расстоянии к , давайте выполним поиск в глубину от корня.

Мы сохраним путь к корню в стеке и поместим каждую вершину в массив для ее предка на расстоянии к .

Чтобы преобразовать массивы обр.

_к + м [в] в цифрах с _к + м [в] , вы можете хэшировать их, используя boron или unordered_map из массива в число.

Часы работы будут На) , поскольку каждая вершина присутствует в списках обр.

только однажды.

Наличие массива с _к [в] , вы легко можете проверить, что существуют два одинаковых к -поддерево.

Для этого найдите две вершины с одинаковыми с _к , в этом случае необходимо рассматривать только вершины, имеющие потомков на расстоянии к от нее (это требование, которое мы отменили вначале).

Чтобы найти максимум к , Давай посчитаем с ₁ [в], с ₂ [в], .

, с ₂ ^т [в] (2 ^т - максимальная мощность двух, не более н ).

После этого используем аналог бинарных лифтов по к : Давайте начнем с к = 0 и по очереди пытайтесь прибавить к нему 2 ^т , 2 ^{т – 1} , .

, 2 ⁰ .

Время выполнения решения: О (нлог (п)) .

Планы на будущее

После этого мы также опубликуем Теги: #Алгоритмы #программирование #mail.ru #спортивное программирование #анализ задач #rcc2017 #rcc #rcc #rcc #russian code cup #russian code cup #russian code cup

• Основные Компоненты Поискового Маркетинга

  19 Oct, 24

• Байки Из Дежурного Склепа

  19 Oct, 24

• Ложные Обещания, Агрессивная Реклама, Троянские Загрузчики И Другие Сюрпризы Google Play

  19 Oct, 24

• Я Не Знаю Ооп

  19 Oct, 24

• 40% Компаний Могут Уйти С Рынка Из-За Цифровой Революции

  19 Oct, 24

• Проблемы Oolp: Неполная Объектная Парадигма И Преждевременная Типизация

  19 Oct, 24

• Windows Internet Explorer 8 Rtw

  19 Oct, 24

• Встреча Сообщества Дизайнеров Dgtl В Райффайзенбанке: Трансляция

  19 Oct, 24

• Голливудское Агентство Будет Искать Таланты В Социальных Сетях

  19 Oct, 24

• Pwc: 80% Российских Клиентов Интернет-Ритейлеров Выбирают Товары В Обычном Магазине, Но Покупают Их Онлайн

  19 Oct, 24