Что ж, продолжаем.
Подойдём ближе к тому, что делает гидродинамику весьма привлекательной снаружи, и постараемся добавить как можно больше красивых и условно красивых картинок.
Еще немного теории будет написано в тексте на примере задачи об устойчивости течения в плоском канале.
В действительности таких задач великое множество - в слоях и ограниченных полостях различной формы, в вертикальных, горизонтальных и наклонных слоях, в обычных жидких и пористых средах, в проводящей жидкости под действием магнитного поля и в раствор какой-нибудь соли под действием температуры, в полостях под действием произвольно направленной вибрации, на границе двух жидкостей.
В общем, просто перечисление всех подуровней гидродинамики может занять пару часов, и вряд ли ты сможешь все запомнить.
Также будет показано несколько примеров чисто гидродинамической неустойчивости течений, без влияния дополнительных факторов (изображения около 700 кб).
Предыдущие посты были написаны с целью обеспечить математическую и семантическую основу для формул в будущих постах.
Коротко о гидродинамике: помните, с чего все начиналось? Коротко о гидродинамике: уравнения движения Кратко о динамике жидкости: сохранение энергии Теория устойчивости вообще представляет собой очень широкую область, которая встречается как в теоретической механике, так и в теориях линейных и нелинейных колебаний (где она наиболее развита).
Особое место в ней занимает теория гидродинамической устойчивости, обусловленная спецификой изучаемого объекта и соответствующих систем уравнений.
Давайте рассмотрим пару самых простых (и, возможно, самых фундаментальных) примеров.
Устойчивость двумерного течения
Пусть имеется произвольное течение несжимаемой вязкой жидкости.
Вполне естественно, что оно описывается уравнениями Навье-Стокса: 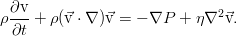
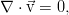
Уравнения по-прежнему даны в размерной форме.
Но для дальнейшей работы их удобно обезразмерить, т. к.
эта операция уменьшает количество параметров и сразу позволяет установить, какие механизмы наиболее значимы в поведении системы.
Процедура обезразмеривания сводится к перемасштабированию всех переменных таким образом, чтобы минимизировать количество параметров.
Чаще всего определяющим фактором является масштаб времени – в качестве его единицы можно выбрать характерное время, в течение которого поток с характерной скоростью пройдет некоторую характерную длину канала (для краткости назовем его кинематическим, так как оно определяется по школьному соотношению время = расстояние/скорость, но такой термин нигде не встречается), время передачи импульса (вязкое время), тепла (тепловое время), внешнего воздействия и т. д. Для уравнений движения в канале удобнее всего взять кинематические времена, указать какую-нибудь условную шкалу скорости и длины, а шкалу давления выбрать исходя из наибольшего упрощения уравнения: 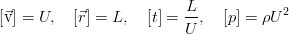
Подставив в уравнение масштабы и уменьшив по плотности и множителю перед нелинейным членом, мы увидим, что все коэффициенты становятся равными единице, за исключением вязкого члена.
Там возникает комбинация параметров, выражающая обратное число Рейнольдса: 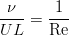
Второе уравнение не изменит своей формы в безразмерном виде.
Таким образом, число Рейнольдса оказывается единственным параметром, определяющим поведение системы.
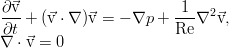
Самое крутое, что только этот один параметр отвечает за ламинарность или турбулентность потока, а уравнения не меняются ни на грамм.
Предположим далее, что имеется некоторый стационарный стационарный поток со скоростью 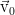
, и существуют бесконечно малые возмущения этого потока: 
В таком виде в систему можно смело подставить скорость и давление, отбросить все, что содержит только стационарные поля скорости и давления, поскольку они сами по себе удовлетворяют уравнениям, а пренебрежение нелинейным членом — важнейший ход во всей теории.
Поскольку мы предполагаем, что возмущения бесконечно малы, то слагаемое вида 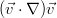
становится бесконечно малым второго порядка.
Поэтому, говоря, что мы работаем в области, где возмущения еще можно считать малыми (т.е.
в самом-самом начале развития будущих неустойчивостей), мы можем смело отбросить нелинейность.
В результате остаются два линейных уравнения, хотя и с переменными коэффициентами: 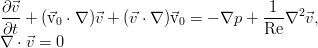
Эта система является основной системой уравнений линейной теории гидродинамической устойчивости и описывает наиболее общие ситуации.
Рассмотрим теперь еще одну конкретную ситуацию — устойчивость плоскопараллельного течения в некотором канале.
Все происходит в самолете( Икс , я ), и вдоль оси й канал бесконечно протяженный — т. е.
чисто двумерный поток.
Пусть стационарное решение имеет только одну компоненту, зависящую от поперечной координаты канала, а возмущения имеют две компоненты: 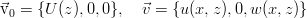
Принимаем также (поскольку уравнения линейны и типичным решением для них является экспоненциальная) экспоненциальную зависимость от времени 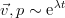
.
Такие нарушения обычно называют «нормальными», хотя история этого термина довольно туманна.
Подставив указанную зависимость и записав уравнения в проекциях на оси, получим систему для плоских возмущений.
При этом коэффициенты в нем не зависят от координаты Икс , поэтому можно дополнительно предположить, что возмущения периодические вдоль этой оси – фактически это близко к разложению в ряд Фурье и рассмотрению только одной компоненты: 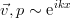
.
В результате получается такая система, уже из обыкновенных дифференциальных уравнений (штрих обозначает производную по я ): 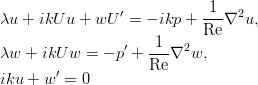
Опуская промежуточные преобразования, несложные, но занимающие пару страниц, отметим, что эту систему можно свести к одному уравнению для компоненты скорости ш : 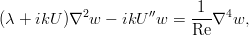
Если записать в него комплексное приращение и ввести фазовую скорость возмущений 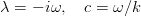
полученное уравнение известно как уравнение Орра-Зоммерфельда: 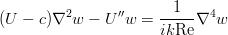
На этом уравнении основана вся линейная теория гидродинамической устойчивости течений.
Правда, точных решений для нее нет, независимо от типа стационарного течения и граничных условий, хотя внешне все выглядит предельно просто и задача закрыта.
Существовали разные подходы к решению этой проблемы.
Например, Рэлей просто пренебрег правой частью в приближении большого числа Рейнольдса.
Конечно, это не всегда правильно, поскольку четвертые производные легко могут сократить знаменатель.
Правда, решить уравнение нам все равно не удалось, но удалось доказать теорема о необходимом условии устойчивости течения .
Правда, для течения Пуазейля это условие не выполняется, но оно все равно может быть неустойчивым.
В том же приближении можно расширить разложение через обратное число Рейнольдса как малый параметр.
В нулевом порядке этого разложения мы получаем упомянутую задачу Рэлея, а если пойти немного дальше, то можно поймать на плоскости параметров две кривые ( к , Re), между которыми возникнет область неустойчивости течения, в которой возмущения возрастают и приводят к разрушению стационарного профиля 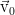
.
Сначала Гейзенберг (тот самый Вернер Гейзенберг, создатель матричной квантовой механики) пытался решить эту задачу для потока Пуазейля, но завершить расширение ему не удалось.
В результате в 1944 году терпеливый китаец Линь Цзя-Цзяо взялся за дело, растянул расширения еще немного и экстраполировал обе кривые, которые сомкнулись в одну.
У него получилось что-то вроде этого (сплошная линия): 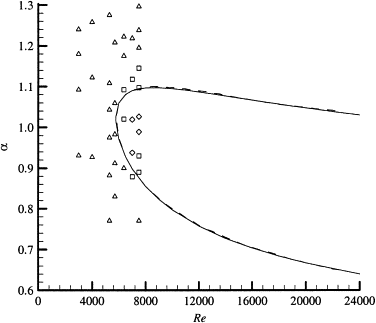
На самом деле этот график для несколько другой системы - вместо обычной жидкости авторы рассматривали взвесь некоторых волокон в канале, но смысл тот же и существенных качественных отличий от теории Линя нет (иллюстрация из работы Ю Чжэньцзянги, Линь Цзяньчжонги, Ю Чжаошенга.
Гидродинамическая неустойчивость волокнистых суспензий в русловых течениях .
Исследования гидродинамики, том 34 (4), 2004 г.
, стр.
251–271).
Вообще течение Пуазейля практически для любой жидкости обладает такими свойствами устойчивости, что лишь подчеркивает фундаментальность результатов Линя.
Примеры нестабильностей
Ниже будут картинки, в основном взятые из «Альбома потоков жидкости и газа» (М.Ван Дайк) и просто из Интернета, с небольшими комментариями по конкретным постановкам задач.
Развитие неустойчивости течения Пуазейля.
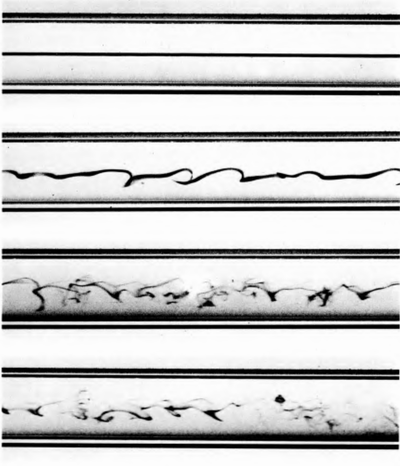
Этот эксперимент был проведен Рейнольдсом в 1883 году.
Фотографии были сделаны на той же самой установке, которая благополучно сохранилась, примерно сто лет спустя.
Сверху вниз на фотографиях скорость течения увеличивается.
В поток вводится тонкая тонированная струя, что позволяет прекрасно визуализировать течение.
Неустойчивость столба жидкости (задача Рэлея-Плато)
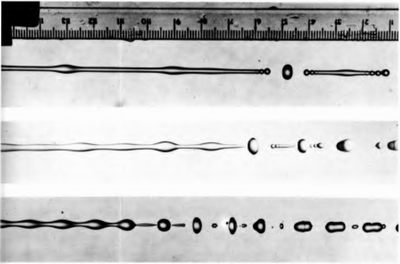
Очень изящная нестабильность, которую мы можем видеть каждый день.
Достаточно открыть кран, чтобы струя была ровной и тонкой, но в то же время достаточно продолжительной.
Из-за взаимодействия случайных возмущений и капиллярных сил сплошной поток стремится разбиться на мелкие капли, поскольку это энергетически более выгодно.
Здесь жидкость возмущается громкоговорителем, к которому подключена выпускная трубка.
Длина волны возмущения на нижнем рисунке близка к теоретическому критическому значению.
Нестабильность Рэлея-Тейлора



Достаточно простая ситуация – тяжелую жидкость выливаем на поверхность легкой жидкости.
Совершенно очевидно, что тяжелый будет стремиться «упасть» вниз, хотя пока этому процессу может противодействовать поверхностное натяжение.
А вот когда движение начинается, это происходит очень красиво, как в лабораториях и расчетах, так и в природе (второй снимок перевернут, по замыслу его автора-фотографа).

Аналогичное явление наблюдается, если в среде имеются две области с очень разными давлениями — вещество «проталкивается» через границу раздела между ними и порождает структуры, подобные простому «проваливанию».
Вихри Тейлора

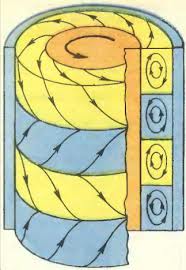
Еще один вариант нестабильности, чем-то схожий по происхождению с Рэлеем-Тейлором.
Жидкость находится между двумя соосными цилиндрами и приводится в быстрое вращение.
За счет центростремительных ускорений в среде, первоначально неподвижной относительно стенок цилиндра, образуются кольцевые ячейки с противоположными направлениями потока.
Нестабильность Кельвина-Гельмгольца
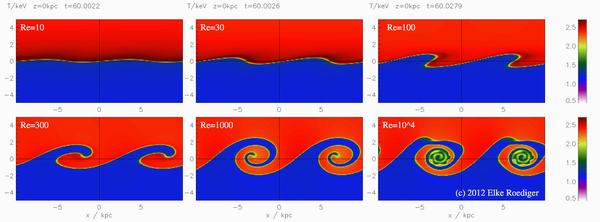


И еще одна версия нестабильности.
Кроме того, физически это очень просто.
Имеем два потока несмешивающихся жидкостей, движущихся навстречу друг другу.
Или просто на разных скоростях – т.е.
на границе между ними происходит скачок скорости, из-за которого возмущения поверхности деформируются, закручиваются и порождают замысловатые вихри, а затем полностью перемешивают жидкости.
Столь же интересно это выглядит и в расчетах, и в экспериментальной установке, и в природе.
Здесь, конечно, показан не весь спектр возможных неустойчивостей – область неисчерпаема и содержит огромный спектр до сих пор неизученных явлений и их особенностей.
Следующий пост будет о конвекции и связанных с ней нестабильностях, вызванных температурной неоднородностью в системе.
Теги: #Популярная наука #физика #гидродинамика #механика жидкости #механика жидкости #механика жидкости #динамика жидкости #динамика жидкости #динамика жидкости
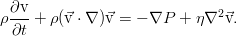
-
Правило Вант-Гоффа
19 Oct, 24 -
Евангелие От Аутиста
19 Oct, 24 -
5 Лучших Видео По Работе С Людьми В Фотошопе
19 Oct, 24 -
Ibm Меняет Формат Сотрудничества С Китаем
19 Oct, 24


