Привет, Хабр! В нашей работе часто возникает необходимость идентификации сообществ (кластеров) различных объектов: пользователей, веб-сайтов, товарных страниц интернет-магазинов.
Польза от такой информации весьма многогранна – вот лишь несколько сфер практического применения качественных кластеров:
- Определение сегментов пользователей для таргетированных рекламных кампаний.
- Использование кластеров в качестве предикторов («признаков») в персональных рекомендациях (в методах, основанных на контенте, или в качестве дополнительной информации при совместной фильтрации).
- Уменьшение размерности в любой задаче машинного обучения, где функциями являются страницы или домены, посещаемые пользователем.
- Сравнение URL-адресов товаров разных интернет-магазинов с целью выявления среди них групп, соответствующих одному и тому же товару.
- Компактная визуализация — человеку будет легче воспринимать структуру данных.

С точки зрения машинного обучения получение таких связанных групп выглядит как типичная задача кластеризации.
Однако мы не всегда имеем легкий доступ к наблюдательным объектам, в пространстве которых можно было бы искать скопления.
Получение контентных или семантических характеристик является весьма трудоемким, как и интеграция различных источников данных, из которых эти функции могут быть получены.
Но у нас есть DMP под названием Facetz.DCA , где факты посещения страниц пользователями лежат на поверхности.
Из них легко получить количество посещений сайтов, как индивидуально, так и совместно для каждой пары сайтов.
Этой информации уже достаточно для построения графиков веб-доменов или страниц товаров.
Теперь задачу кластеризации можно сформулировать как задачу выявления сообществ в полученных графах.
Забегая вперед, скажу, что нам уже удалось с большой пользой использовать веб-сообщества в RTB-рекламных кампаниях.
Классическая проблема, с которой сталкиваются трейдеры, — это необходимость лавировать между точностью таргетинга и размером сегмента.
С одной стороны, грубый таргетинг, основанный на социально-демографических характеристиках, слишком широк и неэффективен.
С другой стороны, сложные тематические сегменты зачастую оказываются слишком узкими, и изменения порогов вероятности в классификаторах не способны расширить сегмент до необходимого объема (скажем, до нескольких десятков миллионов куков).
В то же время люди, часто посещающие домены из одного кластера, формируют хорошие сегменты для столь масштабных кампаний.
В этой серии постов я постараюсь больше сосредоточиться на алгоритмической стороне проблемы, чем на бизнес-стороне, и сделаю следующее.
Сначала опишите наши эксперименты и покажите полученные фотографии.
Во-вторых, подробно рассказать о методах: что мы использовали/хотели использовать, но передумали/хотим использовать в будущем.
Многим из вас, вероятно, приходилось кластеризовать данные, но большинству, как и нам, вероятно, никогда не приходилось кластеризовать график.
Основной особенностью кластеризации графов является отсутствие признаков наблюдения.
У нас нет расстояния между двумя произвольными точками пространства, потому что нет самого пространства, нет нормы и невозможно определить расстояние.
Вместо этого у нас есть метаданные ребер (в идеале для каждой пары вершин).
Если есть «вес» ребра, то его можно интерпретировать как расстояние (или, наоборот, как сходство), и тогда мы определили расстояния для каждой пары вершин.
Многие алгоритмы кластеризации в евклидовом пространстве подходят и для графов, поскольку эти алгоритмы требуют знания только расстояния между наблюдениями, а не между произвольными «точками в пространстве».
Некоторые требуют пространства признаков и не подходят для графиков (например, k-средние).
С другой стороны, графы обладают множеством своих уникальных свойств, которые также можно использовать: компоненты связности, локальные скопления ребер, места закольцовывания потоков информации и т. д.
Обзор инструмента
На сегодняшний день люди изобрели огромное количество методов кластеризации графов — каждый из них имеет свои преимущества и недостатки.В одном из следующих постов мы более подробно рассмотрим некоторые алгоритмы и их свойства.
А пока считаем полезным поделиться ссылками на открытые инструменты для анализа графов, где уже что-то реализовано для кластеризации и поиска сообществ.
- Очень модно и развивается нынче ГрафX .
Его нужно было записать первым элементом в списке, но как таковых готовых алгоритмов кластеризации там пока нет (версия 1.4.1).
Есть подсчет треугольников и компонент связности, который вместе со стандартными операциями на Spark RDD можно использовать для написания собственных алгоритмов.
На данный момент у GraphX есть только API для Scala, что также может затруднить его использование.
- Библиотека для Апач Жираф уполномоченный Окапи использует несколько алгоритмов, включая довольно новый запатентованный алгоритм под названием Спиннер , на основе распространения меток.
Giraph — это надстройка Hadoop, предназначенная для обработки графов.
В нем почти нет машинного обучения, и Telefonica создала Okapi, чтобы компенсировать это.
Вероятно, сейчас Giraph уже не выглядит таким многообещающим по сравнению с GraphX, но сам алгоритм Spinner хорошо вписывается в парадигму Spark. Вы можете прочитать о Spinner Здесь .
- Библиотека граф-инструмент для Python содержит несколько новых алгоритмы кластеризации и работает очень быстро.
Мы использовали его для сравнения URL-адресов, соответствующих одному и тому же продукту.
Все, что возможно, распараллеливается по ядрам процессора, и для локальных вычислений (графы размером до пары сотен тысяч узлов) это самый быстрый вариант.
- Гефи – это хорошо известный инструмент, который мы проигнорировали, возможно, незаслуженно.
Долгое время Gephi практически не развивался, но сейчас у него есть хорошие плагины, в том числе и для выявление сообществ .
Недавно проект снова ожил и ожидается версия 0.9.
- GraphLab Создать .
Это оболочка Python над C++, которая позволяет запускать машинное обучение как локально, так и распределенно (на Yarn).
Кластеризации графов там по-прежнему нет, только поиск k-ядер .
- Хваленая сетьX, несмотря на обилие алгоритмы , не может кластеризовать графы, а только анализировать связные компоненты и клики.
Кроме того, он значительно медленнее граф-инструмента, а по визуализации уступает граф-инструменту и gephi.
- Реализация алгоритма Марковская кластеризация (MCL) от его изобретателя.
Автор уменьшил сложность обычного MCL в худшем случае с помощью
до
, Где
- количество узлов, и
— максимальная степень узла, и обижается, когда алгоритм MCL называют немасштабируемым.Он также добавил функции для регулировки количества кластеров.
Однако у MCL было несколько других серьезных проблем, и неясно, были ли они решены.
Например, проблема нестабильности размера кластера (наш небольшой эксперимент дал одну гигантскую компоненту связности и множество маленьких кластеров по 2-3 узла, но, возможно, мы не нашли нужную ручку).
Последние новости на сайте относятся к 2012 году, что не очень хорошо.
- Различные реализации одного из самых популярных алгоритмов Лувена: для С , для Python , больше для Python .
Классическая статья об этом алгоритме: связь .
- Веб-сайт , посвященный алгоритму Infomap и его модификациям, от авторов метода.
Как и все остальное, это открытый исходный код. Помимо хорошей поддержки и документации, есть потрясающие демо, иллюстрирующие работу алгоритма: Здесь И Здесь .
Вы можете узнать, как работает алгоритм Здесь .
- Пакет для R под названием граф .
В нем реализовано довольно много алгоритмов кластеризации, но мы не можем сказать о них ничего конкретного, так как не изучали пакет.
Наши эксперименты
А сейчас мы расскажем, как мы формировали графы доменов Рунета и прилегающей территории, и покажем картинки с результатами их кластеризации.В следующей части нашей серии статей будет описан алгоритм, с помощью которого были получены картинки ниже.
Это модифицированный k-medoids, который мы, в лучших велосипедных традициях, написали на корневом Python, и с помощью которого нам на удивление хорошо удалось решить некоторые задачи.
Часть информации из этого и следующего поста, а также описание некоторых других алгоритмов есть в презентации, которую я провел на newprolab в цифровом октябре этой весной:
Данные
Первая задача — кластеризация веб-доменов.Из DMP мы берем данные о посещениях пользователями различных доменов и на их основе строим граф, где домены выступают узлами, а сходства между доменами — ребрами.
Сходство (или лифт) между доменами
И
представляет собой выборочную оценку того, в какой степени события, «посещенные пользователем»
домен
" и "посещение пользователя
домен
"близок к независимости.
Если
- общее количество рассматриваемых пользователей, и
— количество пользователей, посетивших
, Что:
Чтобы избавиться от шума, нужно отфильтровать домены со слишком малым количеством посещений, а также ребра с низкой близостью.
Практика показывает, что порога 15-20 для посещений и 20-25 для близости достаточно.
Более высокий порог сходства приводит к появлению слишком большого количества изолированных вершин.
Такой способ построения графа позволяет увидеть в данных достаточно четкую структуру «сообществ» доменов.
Одна из его интересных особенностей заключается в том, что самые крупные домены (поисковые системы, социальные сети, некоторые крупные магазины и новостные сайты), как правило, не имеют очень «толстых» ребер с какой-либо другой вершиной.
Это приводит к тому, что эти домены находятся на окраинах и часто остаются изолированными вершинами, не попадая ни в один из кластеров.
Мы считаем это плюсом, так как совместное посещение ВК и какого-то узкоспециализированного сайта действительно мало что говорит об их связи друг с другом.
Надо сказать, что получение и фильтрация данных, построение графа и вычисление из него различных матриц — гораздо более ресурсоемкая задача, чем получение самих кластеров.
Некоторые этапы (в частности, вычисление попарного сходства) были распараллелены с помощью пакета pathos ( пафос.
мультипроцессинг ).
В отличие от стандартного пакета многопроцессорности Python, он не страдает от проблем сериализации, поскольку вместо рассола используется укроп.
Его синтаксис абсолютно идентичен стандартному многопроцессорному режиму.
Здесь вы можете прочитать об укропе.
Визуализация
Пришло время показать несколько картинок с графиками (как они получились, мы расскажем в следующей части).Известно, что networkX не предназначен для визуализации графов, и для этой цели лучше обратиться к d3.js, gephi или Graph-Tool. Мы узнали об этом слишком поздно и вопреки здравому смыслу все равно смело продолжали рисовать картинки в networkX. В результате получился не совсем чистый мёд (в частности, не удалось настроить взаимное отталкивание узлов и непересекающиеся метки), но мы постарались и выжали всё возможное из возможностей networkX. На всех картинках диаметр кружка (домена) соответствует его трафику, толщина края соответствует аффинности, цвет кружка означает принадлежность домена к кластеру.
Цвет ребра означает, что обе вершины принадлежат данному кластеру; серый цвет соответствует ребрам, соединяющим вершины из разных кластеров.
Комментарии к кластерам на примере одного из графиков
Не очень большой график из 1285 доменов:
На картинке показан его разреженный вариант: большая часть ребер удалена методом локальной разреженности (о нем будет рассказано в следующей части), поэтому группировка в сообщества выглядит более отчетливой и эффект «Больших волос» Мяч» смягчается.
Кластеров всего 18. Полный размер картинки (в формате png).
На каждом узле написано имя домена и номер кластера, к которому он принадлежит. Обратите внимание на изолированные вершины по внешнему кругу — это, как правило, большие домены, ни с кем не имеющие прочной связи.
Нижнюю часть графика можно охарактеризовать как более «женскую» (вернее, «семейную»).
Это довольно запутанно, вероятно, потому, что страницы просматривались несколькими членами семьи в разное время в одном и том же браузере (с одним и тем же файлом cookie).
Алгоритм не очень хорошо справился с идентификацией сообществ в этой части графа.
В одном огромном кластере под номером 17 (розовый) собрано много всего — от сайтов о беременности внизу и медицинских сайтов в центре, до мешанины прогнозов погоды, женских форумов и журналов вверху кластера.
«Юго-западнее» от него расположен кулинарный кластер (№4): 
К «юго-востоку» семейного кластера – недвижимость + поиск работы (объединены в один кластер №2): 
«Южнее» кластера 17 находится очень плохо выраженная область.
Так, алгоритму не удалось идентифицировать сообщество туристических доменов (они разбросаны по разным сообществам), а сайт об оружии попал в кулинарный кластер.
Небольшой кластер 15 (красный) включал в себя в основном легальные сайты: 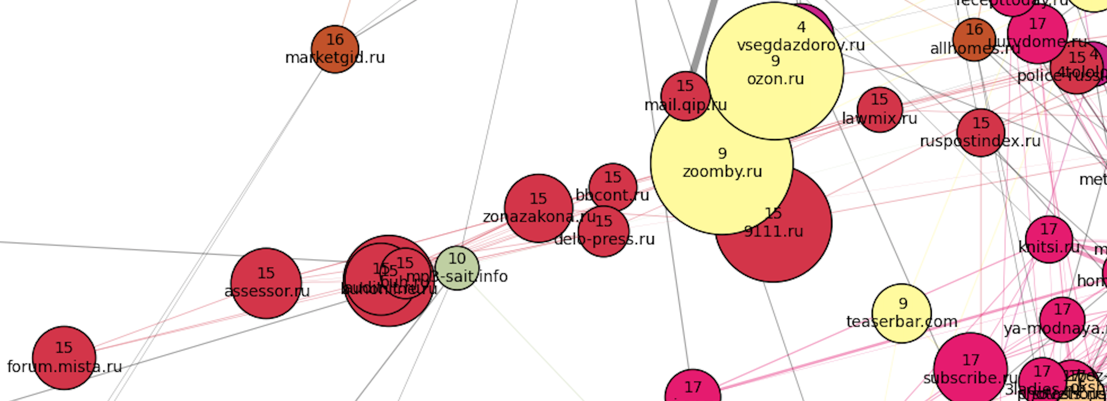
Наиболее четкие скопления расположены «северо-западнее» «семейной» части.
Судя по всему, браузерами посетителей этих сайтов уже никто не пользуется (и это логично, исходя из тематики кластеров).
Во-первых, бросаются в глаза два плотных кластера: российские (номер 16, кирпичик) и украинские (номер 12, синий) новостные сайты, причем последний гораздо плотнее, хотя и меньше по размеру.
Также можно заметить, что меняется смещение площадок по российскому кластеру: 
К «северо-востоку» от новостных сайтов расположены фильмы, сериалы и онлайн-кинотеатры (серые и желтые кластеры под номерами 3 и 8).
Между кинокластерами и украинским новостным кластером в качестве переходной зоны располагается порнокластер.
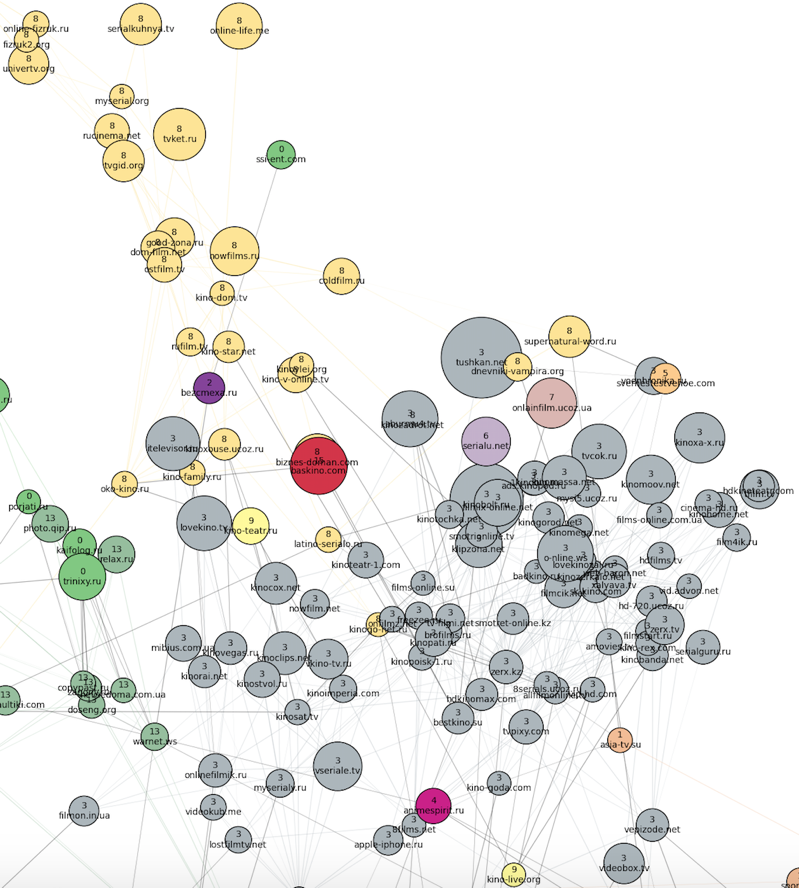
Еще дальше на восток находится кластер номер 1 — весь казахстанский Интернет. Рядом расположены автомобильные сайты (кластер 6, сиреневый) и российские спортивные сайты (они присоединились к остальным новостям в кластере 16).
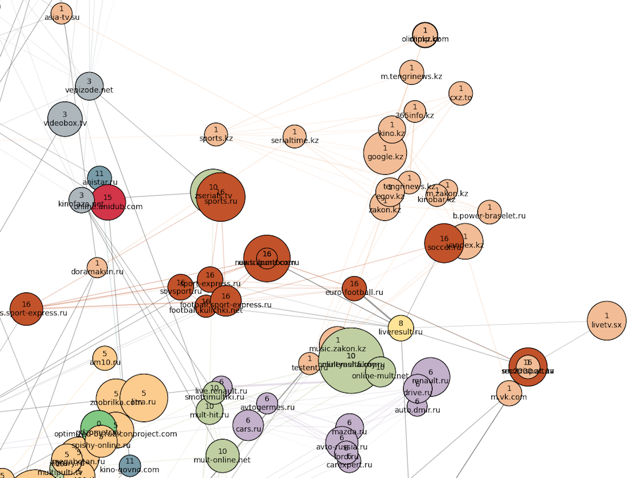
Южнее находится кластер мультфильмов и детских игр (цифра 10, болото), а также тесно связанные с ним школьные кластеры словарей, онлайн-решателей и конспектов: большой русский (цифра 5, персиковый) и совсем маленький украинский.
один (цифра 0, зеленый).
В кластер №0 также вошли украинские сайты всех тематик, кроме новостных (их было очень мало).
Школьные кластеры «юга» плавно переходят в основной женский кластер № 17. 
Последнее, что здесь можно отметить, это скопление книг, расположенное на окраине «восточной» части картины: 
Изменения за год
Вот как выглядит тот же график, только нарисованный без прореживания:
Полный размер.
А вот так выглядит примерно аналогичный график, построенный почти за год до предыдущего.
Он имеет 12 кластеров: 
Полный размер.
Как видите, за это время структура в целом осталась прежней (новостные сайты, большой женский кластер, большая разреженная территория развлекательных сайтов разного типа).
Среди отличий можно отметить окончательное исчезновение кластера с музыкой за это время.
Вероятно, за это время люди практически перестали пользоваться специализированными сайтами для поиска музыки, чаще обращаясь к социальным сетям и развивающимся сервисам вроде Spotify. Разделимость всего графа на сообщества в целом увеличилась, а количество значимых кластеров увеличено с 12 до 18. Причины этого, скорее всего, кроются не в изменении поведения пользователей, а просто в изменении наших источников данных.
и механизм сбора данных.
Если увеличить выборку пользователей и оставить фильтры на том же уровне для минимального количества посещений домена и пары доменов, а также минимальной близости для формирования ребра, мы получим более крупный график.
Ниже приведен такой граф из 10121 вершины и 30 кластеров.
Как видите, алгоритм отбора мощности из networkx уже не очень эффективен и выдает довольно запутанную картину.
Однако в такой форме можно проследить некоторые закономерности.
Количество ребер было уменьшено с полутора миллионов до 40 000 с использованием того же метода локального разрежения.
Размер PNG-файла составляет 80 МБ, поэтому просмотрите его в полном размере.

Визуализация не смогла должным образом выделить структуру сообществ (беспорядок в центре), но на самом деле кластеры оказались не менее содержательными, чем в случае с 1285 доменами.
По мере увеличения объема данных наблюдаются интересные закономерности.
С одной стороны, начинают выделяться небольшие периферийные кластеры, неразличимые на небольших данных.
С другой стороны, то, что плохо кластеризовалось на малых данных, плохо кластеризуется и на больших (например, сайты о недвижимости и поиске работы перемешаны, часто к ним соседствуют эзотерика и астрология).
Вот несколько примеров новых сообществ.
На самой окраине выделялось испанское скопление, кое-что мы видим оттуда: 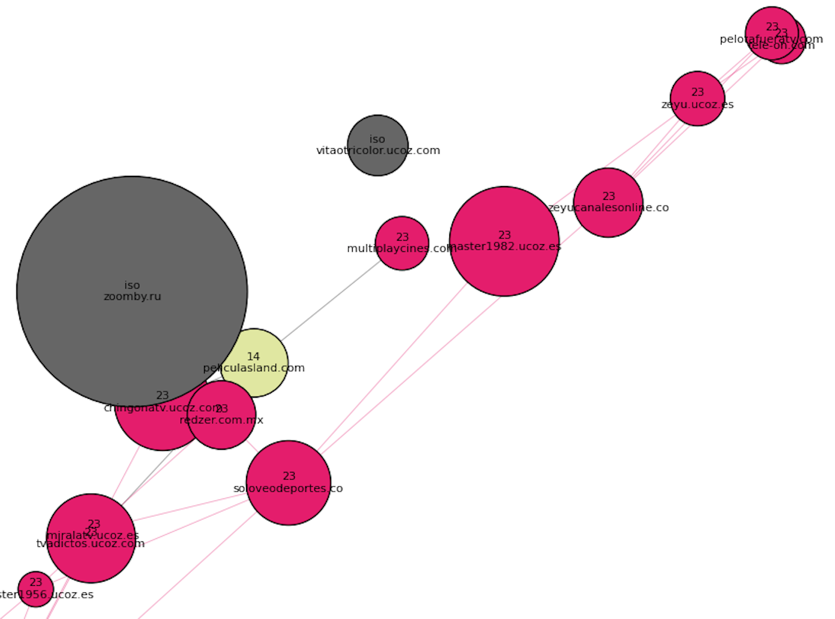
Недалеко от него, ближе к основному скоплению точек, расположены азербайджанский кластер (номер 2) и грузинский (номер 4): 
Появился узбекско-таджикский кластер, а также белорусский (номер 16) – внутри основной массы доменов, рядом с «российскими новостными» и «украинскими неновостными» сообществами: 
В следующем посте будет описан алгоритм:
– как были получены сами кластеры, чтобы таким образом можно было раскрасить граф;
– как удаляли лишние ребра.
Мы готовы ответить на ваши вопросы в комментариях.
Следите за обновлениями! Теги: #обнаружение сообщества #Кластеризация #СНС #графы #опрос #визуализация #Интеллектуальный анализ данных #Большие данные #Визуализация данных #Машинное обучение

-
Трудности Перевода Антивируса
19 Oct, 24 -
Новые Технологии Для Моторных Масел Лукойл
19 Oct, 24 -
Открытие Ит-Клуба Modx В Екатеринбурге
19 Oct, 24


