Когда я разговариваю с человеком, далёким от физики, о возможных, неизвестных нам дополнительных измерениях пространства, один из наиболее часто задаваемых вопросов: «Как вы представляете себе дополнительные измерения? Я могу думать только о трёх и не вижу, как мне идти дальше; Это не имеет никакого смысла для меня.
" Чего мы, физики, не делаем (по крайней мере, никто из моих знакомых этого не утверждает), так это воображаем дополнительные измерения.
Мой мозг ограничен так же, как и ваш, и хотя этот мозг легко может создать трехмерное изображение мира, в котором я могу двигаться, я не могу заставить его создать изображение четырех- или пятимерного мира, как ты.
Мое выживание не зависело от способности представить что-то подобное, поэтому, возможно, неудивительно, что мой мозг не приспособлен к этому.
Вместо этого я (и, судя по нашему обмену идеями, большинство моих коллег тоже) развиваю интуицию, основанную на сочетании аналогий, приемов визуализации и расчетов.
Мы опустим здесь расчеты, но многие аналогии и хитрости объяснить не так уж сложно.
Размышлению о дополнительных измерениях можно научиться в два этапа.
- Простой шаг — научиться представлять или описывать мир в дополнительных измерениях.
Вы уже знаете несколько способов сделать это, даже если не осознаете этого, и можете узнать немного больше.
- Более сложный шаг — узнать, как все работает в мире с дополнительными измерениями.
Как работать иглой в четырех измерениях, а не в трех; будут ли планеты вращаться вокруг Солнца в шести пространственных измерениях; образуются протоны и атомы? Здесь вам нужно будет научиться незнакомым трюкам, представляя различия между миром только с одним или двумя измерениями и известным нам трехмерным миром и работая по аналогии.
Для этого нам нужно подумать о том, как мы вообще представляем какое-либо измерение.
Начать сначала.
- Мир с нулевыми измерениями — это точка.
О нем сейчас можно сказать немного, но мы к нему еще вернемся.
- Одномерный мир уже довольно интересен.
- В 2D-мирах происходит гораздо больше интересного.
- Важно избегать путаницы между пространственными измерениями и более общим смыслом слова «измерение» в обычном языке, в математике и статистике.
- Далее последуют различные примеры дополнительных измерений с акцентом на то, что именно означает «дополнительные» и как возможно, что в нашем мире существуют измерения, о которых мы ничего не знаем.
- Мы также посмотрим, как именно можно обнаружить эти тонкие измерения.
Одномерные миры
Мир с одним пространственным измерением гораздо проще мира с тремя, но в нем есть кое-что, о чем можно порассуждать.Например, существует несколько типов одномерных миров.
У них есть не только некоторые общие свойства, но и интересные различия.
В качестве первого примера давайте посмотрим на измерение не как на физическую концепцию, а как на более общую концепцию.
Это поможет вам во многих отношениях, например, отвлечет вашу интуицию от естественных заблуждений о том, что такое измерения и как они работают. Поговорим о годовом заработке – сколько денег человек получает в определенный год. Это измерение так же пригодно для изучения, как и любое другое.
Размер дохода
Ваш доход за последний год — это определенное число в вашей местной валюте.Оно может быть положительным или отрицательным, большим или маленьким; ее можно представить в виде точки на линии, как на рис.
1, которую мы назовем «точкой дохода».
Каждая точка на линии представляет собой возможный доход. 
Рис.
1: линия прибыли бесконечной длины, левая сторона которой представляет убытки, правая сторона представляет доход. Что делает годовой доход одномерным свойством (очень грубо говоря) следующее: • Положение в пространстве обозначается одной единицей информации: в нашем случае доходом.
Также отметим, что он непрерывен (или почти непрерывен) — если два человека имеют разные доходы A и B, мы можем найти третьего, чей доход находится между A и B. Эти два факта подразумевают, что доход может непрерывно меняться вдоль линии дохода, перемещаясь вправо или влево – либо к более высокому, либо к более низкому доходу.
Других вариантов нет. Конечно, линия дохода не имеет ничего общего с физическим пространством, в котором мы с вами можем ходить, но это все же измерение.
И (по крайней мере, в принципе) оно не имеет конца ни в том, ни в другом направлении: нет (в принципе) предела тому, сколько денег человек может заработать или потерять за год. Этот одномерный мир не так уж и разнообразен, но мы все же можем задать о нем несколько значимых вопросов:
- Как распределяется годовой доход в США?
- Какой средний годовой доход в Японии?
- Как ответы на эти вопросы меняются со временем?
Радужное измерение
И вот другой, совершенно другой мир.Единое измерение образуют цвета радуги: от красного через оранжевый к желтому, оттуда к зеленому, [голубому], индиго и фиолетовому [англоязычные люди имеют шесть цветов радуги, они не различают синий / ок.
перевод].
С этой точки зрения цвета образуют одномерный мир конечного размера.
За красным и фиолетовым есть невидимые формы цветов, но с точки зрения ваших глаз на этом измерение заканчивается.
Теперь она представлена не бесконечной линией, а отрезком – «радужной линией» на рис.
2. Пожалуйста, не путайте ее с цветовым кругом – если он замкнут, то наше измерение начинается с красного цвета и заканчивается фиолетовым.
.
Опять же, положение на радужной линии определяется одним фрагментом информации (цветом) и является непрерывным.
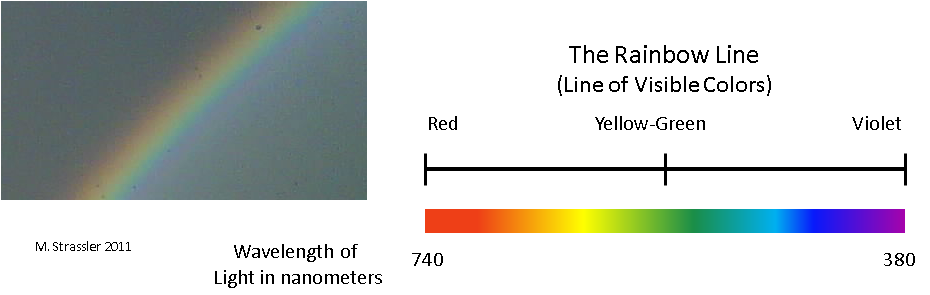
Рис.
2 Очевидно, это также не измерение физического пространства! Вы можете перекинуть мяч из своего дома в дом соседа, но не можете себе представить, как перебрасываете мяч из зеленого в оранжевый — это не имеет смысла.
И все равно это тоже будет измерение.
Здесь можно задать много важных вопросов: как цвет яблока меняется вдоль линии радуги, когда яблоко меняет цвет с зеленого на красный? Сколько каждого цвета присутствует в солнечном свете? Если оранжевая звезда начнет краснеть, пожелтеет ли она первой?
Измерение направления ветра
Но вот третий вариант измерения, и опять другой.Если вы послушаете прогноз погоды, то вам скажут, что скоро ветер начнет дуть с севера, или с северо-запада, или с юго-запада.
Возможные направления ветра также являются измерением.
Обратите внимание, что это не пространственное измерение! В этом измерении вы не можете бросить мяч так, как вы его бросаете вверх, влево или вперед. Это измерение направлений в пространстве! 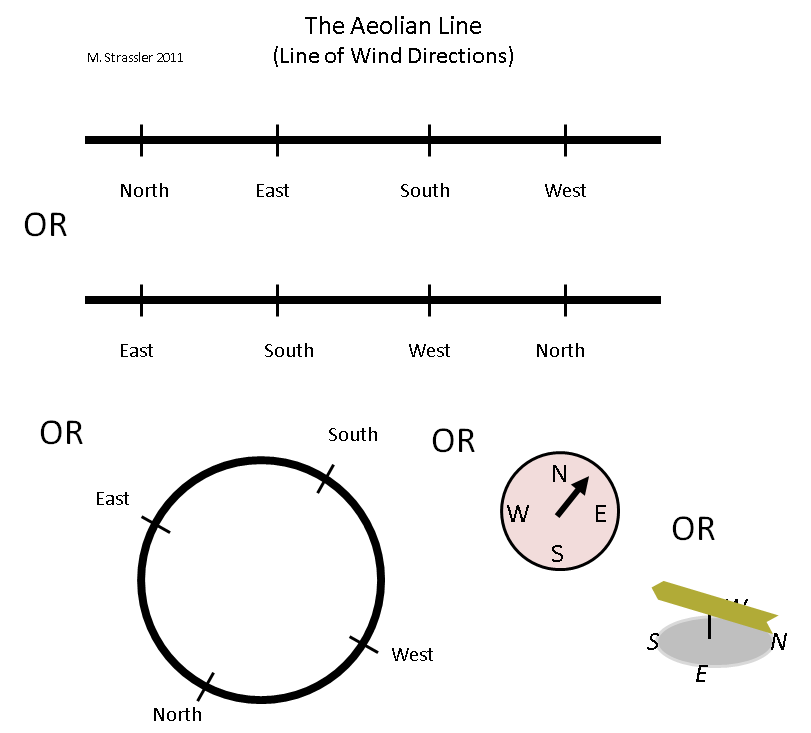
Рис.
3 Как мы можем представить это измерение? Есть как минимум два естественных способа сделать это, показанных на рис.
3. Один использует отрезок – «эоловую линию» ( Эол — полубог, повелитель воздушной стихии у древних греков) — но эолова линия отличается от радужной своей периодичностью.
Направление ветра может непрерывно меняться с севера на восток, затем на юг, затем на запад, а затем снова на север.
И, на наш взгляд, линию можно разрезать где угодно — сравните две линии вверху рис.
3, одинаково хорошо изображающие эоловую линию.
Дело в том, что ветер может идти от правого конца лески прямо к левому концу и наоборот, поэтому не имеет значения, где вы ее перережете.
Или, возможно, проще всего представить эту периодическую линию как круг.
Именно это мы и делаем с компасом или флюгером!
Три разных одномерных мира
И вот вам одномерные миры.Посмотрите, насколько они богаты деталями! Разные размеры, разные свойства.
На линии дохода доход может постоянно расти или падать.
На линии радуги ваши глаза могут двигаться только до фиолетового цвета, или наоборот, только до красного.
А на эоловой линии ветер может сколько угодно совершать полный круг – но при этом всегда будет возвращаться в одно из направлений.
Эти разновидности одномерных миров — бесконечные, конечные и конечно-периодические, представленные бесконечной линией, сегментом и кругом, — являются основными ингредиентами для понимания миров более высоких измерений.
Я буду обращаться к ним снова и снова.
На рис.
4 показаны они, а также четвертый тип, простирающийся неограниченно только в одном направлении.
Примером такого измерения может быть температура: она может быть сколь угодно большой, но существует минимально возможная температура — абсолютный ноль — поэтому температура образует линию, начинающуюся с абсолютного нуля и идущую оттуда вверх, но не вниз.

Рис.
4
Как изображать размеры, пространственные и другие
Я мимоходом упомянул или использовал несколько различных методов представления измерений.Доход может быть представлен как числом, так и бесконечной линией.
Видимую радугу можно представить в виде сегмента или цвета, а также с помощью числа — длины волны фотонов, соответствующей определенному цвету.
Направление ветра может быть представлено кругом или сегментом, левый конец которого соединен с правым, или такими словами, как север, восток, юг, запад, или числом, определяющим направление в градусах от 0 до 360 и обратно к 0. То, что мы можем представлять одно измерение разными способами, дает нам огромную гибкость для тренировки нашей интуитивной работы с дополнительными измерениями.
Чтобы проиллюстрировать эти типы измерений, я выбрал понятия, не имеющие ничего общего с физическим пространством — доход, цвет радуги, направление ветра — чтобы показать, что пространственные измерения являются конкретными примерами более общей концепции измерения.
Понимание этого факта значительно облегчает попытки представить миры, имеющие более трех измерений.
Помните, как я упоминал две части обучения мышлению о дополнительных измерениях? Сначала научитесь их представлять; во-вторых, понять, как в них все устроено и работает. Пространственные измерения имеют особенности, связанные с тем, как в них работают некоторые вещи, но не с их представлением.
Пространственные миры с одним эффективным измерением
Принимая все это во внимание, давайте рассмотрим пространственные миры, с которыми мы регулярно сталкиваемся, с одним эффективным измерением.Или, точнее, ситуации, в которых определенный аспект нашего мира ведет себя так, как если бы пространство имело только одно измерение.
Затем мы говорим, что мир для некоторых участников или объектов становится фактически одномерным.

Рис.
5 Представьте себе канатоходца, балансирующего на высокой веревке.
Мир канатоходца фактически одномерен (хотя, конечно, на самом деле он все еще трехмерен), поскольку он не может безопасно двигаться ни в каком направлении, кроме справа налево или слева направо.
Этот мир подобен радужному миру - его длина конечна, и когда канатоходец доходит до конца, он должен развернуться и идти назад (или сойти с веревки, попадая в ситуацию, в которой мир становится фактически единым).
размерный).
Что еще можно сказать? Положение на веревке можно определить по одной порции информации (например, расстоянию от левого шеста до канатоходца).
Два канатоходца могут встретиться на одной линии, но не пройти мимо друг друга.
Мы можем превратить мир веревки в эоловую линию, замыкая ее в круг (рис.
6).
В нем два канатоходца также не могли пройти мимо друг друга – это главное свойство одномерных миров.
И это все равно будет конечное измерение.
А вот канатоходец в такой ситуации уже мог ходить по кругу непрерывно и бесконечно, не останавливаясь.

Рис.
6 Другие (фактически) одномерные миры, о которых мы знаем:
- Узкая дорога — это одномерный мир для автомобилей;
- Узкая тропа со скалой – для туриста, поднимающегося на гору;
- этажи многоэтажного дома – для лифта.
В будущем помните: мы живем в кажущемся трехмерном мире, и все, с чем мы сталкиваемся, кажется нам трехмерным.
Но иногда наш трехмерный мир (точнее, его часть) может вести себя как эффективно одномерный, или двумерный (можете придумать примеры?), или даже нульмерный! (Любой, кому когда-либо не везло застрять в беспросветной пробке, знает, что представляет собой этот нульмерный мир!) Эта интуиция нам очень пригодится позже.
Теги: #Популярная наука #физика #измерения #Мэтт Страсслер #Мэтт Страсслер #Мэтт Страсслер #одномерные миры

-
Поиск Лучше: Теперь С Обратными Ссылками
19 Oct, 24


