От переводчика.
Перевод Статьи 2011 года на arxiv.org по статистическому анализу модификации быстрой сортировки.
Наверняка есть люди, которые интуитивно используют описанный вариант. Вот математическое обоснование эффективности для n <= 7,000,000
Введение
Ключевые слова Внутренняя сортировка; Равномерное распределение; Средняя временная сложность; Статистический анализ; Статистическая оценка Сундараджан и Чакраборти [10] представили новую версию быстрой сортировки, исключающую обмены.
Крайзат [1] отметил, что алгоритм хорошо конкурирует с некоторыми другими версиями быстрой сортировки.
Однако он использует вспомогательный массив, увеличивая пространственную сложность.
Здесь мы предоставляем вторую версию, в которой мы удалили вспомогательный массив.
Эта версия, которую мы называем K-сортировкой, упорядочивает элементы быстрее, чем пирамидальная, для массивов больших размеров (n <= 7,000,000) for uniformly distributed input data U[0, 1] (в статистическом смысле – прим.
перев.
) .
1. Введение Существует несколько методов внутренней сортировки (когда все элементы могут храниться в основной памяти).
Простейшие алгоритмы, такие как пузырьковая сортировка, обычно занимают время O(n).
2 ) упорядочивают n объектов и полезны только для небольших наборов.
Одним из наиболее популярных алгоритмов больших множеств является быстрая сортировка, которая принимает O(n*log 2 n) в среднем и O(n 2 ) в худшем случае.
Подробнее об алгоритмах сортировки в Кнуте читайте [2].
Сундараджан и Чакраборти [10] представили новую версию быстрой сортировки, исключающую обмены.
Хрейсат [1] обнаружил, что этот алгоритм хорошо конкурирует с некоторыми другими версиями быстрой сортировки, такими как SedgewickFast, Bsort и сортировка Singleton для n[3000.200000].
Поскольку в алгоритме сравнения доминируют обмены, удаление обменов не делает сложность этого алгоритма чем-то отличным от сложности классической быстрой сортировки.
Другими словами, наш алгоритм имеет среднюю и наихудшую сложность, сравнимую с быстрой сортировкой, то есть O(n*log 2 n) и O(n 2 ) соответственно, что также подтверждает Крейзат [1].
Однако он использует вспомогательный массив, тем самым увеличивая пространственную сложность.
Здесь мы предлагаем вторую улучшенную версию нашей сортировки, которую мы называем K-сортировкой, в которой удаляется вспомогательный массив.
Было обнаружено, что сортировка элементов с помощью K-сортировки происходит быстрее, чем сортировка пирамиды со значительным размером массива (n <= 7,000,000) of uniformly distributed input U[0, 1].
1.1 К-сортировка
Step-1: Initialize the first element of the array as the key element and i as left, j as (right+1), k = p where p is (left+1).Step-2: Repeat step-3 till the condition (j-i) >= 2 is satisfied. Step-3: Compare a[p] and key element. If key <= a[p] then Step-3.1: if ( p is not equal to j and j is not equal to (right + 1) ) then set a[j] = a[p] else if ( j equals (right + 1)) then set temp = a[p] and flag = 1 decrease j by 1 and assign p = j else (if the comparison of step-3 is not satisfied i.e. if key > a[p] ) Step-3.2: assign a[i] = a[p] , increase i and k by 1 and set p = k Step-4: set a[i] = key if (flag = = 1) then assign a[i+1] = temp Step-5: if ( left < i - 1 ) then Split the array into sub array from start to i-th element and repeat steps 1-4 with the sub array Step-6: if ( left > i + 1 ) then Split the array into sub array from i-th element to end element and repeat steps 1-4 with the sub array
Демонстрация
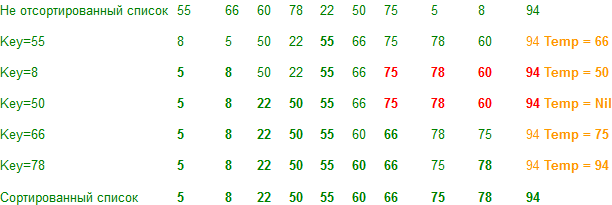
Примечание.
Если вспомогательный массив имеет одно значение, его не нужно обрабатывать.
2. эмпирический (средняя временная сложность) Компьютерный эксперимент представляет собой серию запусков кода для различных входных данных (см.
Сакс [9]).
Borland International Turbo 'C++' 5.02 , мы могли сравнить среднее время сортировки в секундах (среднее значение заняло более 500 операций чтения) для разных значений n в K-сортировке и Heap. Используя моделирование Монте-Карло (см.
Кеннеди и Джентл [7]), массив размера n был заполнен независимыми непрерывными однородными вариациями U[0, 1] и скопирован в другой массив.
Эти массивы были отсортированы сравниваемыми алгоритмами.
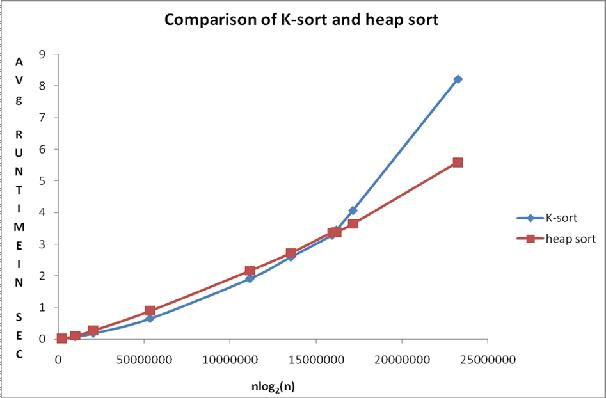
В таблице 1 и на рисунке 1 показаны эмпирические результаты.


Рис.
1 Сравнительная таблица Наблюдаемые средние времена непрерывного равномерного распределения U(0,1) для рассматриваемых сортировок представлены в таблице 1. На рисунке 1 вместе с таблицей 1 показано сравнение алгоритмов.
Точки на графике, построенном на основе таблицы 1, показывают, что среднее время выполнения K-сортировки меньше, чем пирамидальной сортировки, когда размер массива меньше или равен 7 000 000 элементов, а выше этого диапазона пирамидальная сортировка выполняется быстрее.
3. Статистический анализ эмпирических результатов с использованием Minitab версии 15. 3.1. Анализ K-сортировки: регрессия среднего времени сортировки y(K) по n*log 2 (n) и n 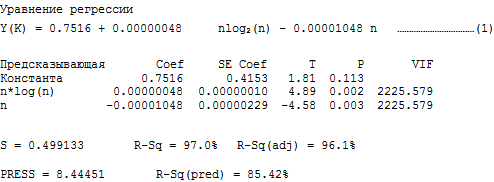

R обозначает наблюдение с большими стандартизированными остатками.
Рис.
2.1-2.4 показаны визуальные итоги некоторых дополнительных испытаний модели.
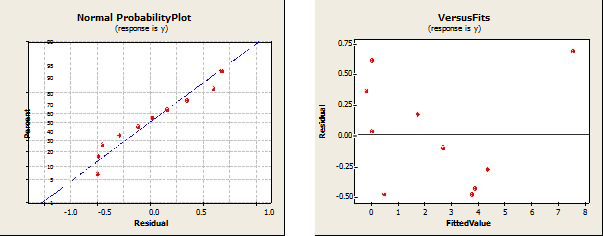
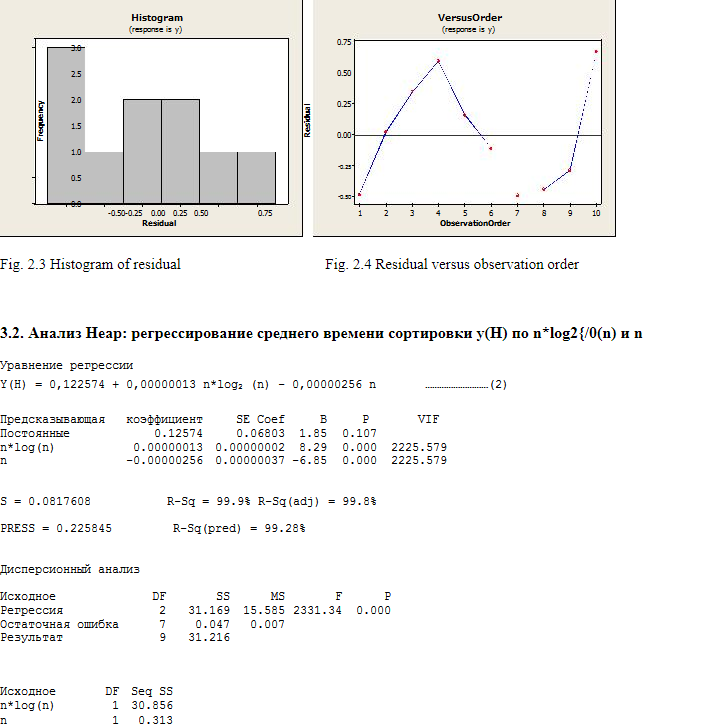

4. Дискуссионная часть
Легко видеть, что сумма квадратов, вносимая n*log(n) в регрессионную модель как в K-сортировке, так и в пирамиде, является значимой по сравнению с суммой, полученной n. Напомним, что оба алгоритма имеют среднюю сложность O(n*log 2 н).
Таким образом, экспериментальные результаты подтверждают теорию.
Мы сохранили член n в модели, поскольку, глядя на математический оператор, сложность которого равна O(nlog).
2 n) в быстрой сортировке и пирамидальной сортировке принимает n-термин (см.
Кнут [2]).
Уравнение регрессии сравнения для среднего случая получается простым вычитанием y(H) из y(K).
Имеем: y(K) – y(H) = 0,52586 + 0,00000035 n*log2(n) – 0,00000792 n …….
(3) Преимущество уравнений (1), (2) и (3) состоит в том, что мы можем предсказать среднее время выполнения обоих алгоритмов сортировки, а также их разницу даже для огромных значений n, которые громоздки в исполнении.
Этот вид «дешевого прогнозирования» является лозунгом компьютерных экспериментов и позволяет нам выполнять стохастическое моделирование даже на неслучайных данных.
Еще одним преимуществом является то, что вам нужно знать только размер входных данных, чтобы сделать прогноз.
То есть весь ввод (для которого фиксируется ответ) не требуется.
Таким образом, прогнозирование с помощью стохастической модели не только дешевле, но и более эффективно (Сакс, [9]).
Важно отметить, что когда мы непосредственно работаем над временем выполнения программы, мы фактически вычисляем статистическую оценку в конечном диапазоне (компьютерный эксперимент невозможно выполнить для входных данных бесконечного размера).
Статистическая оценка отличается от математическая оценка в том смысле, что, в отличие от математической, она взвешивает, а не точно рассчитывает вычислительные операции и, как таковая, способна объединять различные операции в концептуальную оценку, тогда как математическая сложность специфична для операции.
Здесь время работы принимается за его вес.
Общее обсуждение статистической оценки, включая формальное определение и другие свойства, см.
в Чакраборти и Собике [5].
См.
также Чакраборти, Моди и Паниграхи [4], чтобы понять, почему статистическая оценка является идеальным пределом параллельных вычислений.
Допущение статистической оценки получается путем проведения компьютерных экспериментов, в которых весам присваиваются числовые значения в конечном диапазоне.
Это означает, что достоверность соответствующей оценки зависит от правильного планирования и анализа нашего компьютерного эксперимента.
Сопутствующую литературу по компьютерным экспериментам в других областях применения, таких как проектирование СБИС, горение, теплопередача и т. д., можно найти в (Fang, Li and Sujianto, [3]).
См.
также обзор (Чакраборти [6]).
5. Заключение и предложения по дальнейшей работе.
K-сортировка очевидно быстрее, чем Heap, для чисел сортировок до 7 000 000, хотя оба алгоритма имеют одинаковый порядок сложности O(n*log 2 о) в среднем случае.
Будущая работа включает изучение параметризованной сложности (Махмуд, [8]) в этой улучшенной версии.
В качестве последнего комментария мы настоятельно рекомендуем K-сортировку как минимум для n <= 7,000,000. Однако мы согласны выбрать пирамидальную сортировку в худшем случае, поскольку она поддерживает сложность O(n*log).
2 о) даже в худшем случае, хотя его и сложнее программировать.
Б.
Продолжение работы, 2012 г.
Библиография [1] Хрейсат Л.
, QuickSort: историческая перспектива и эмпирическое исследование, Международный журнал компьютерных наук и сетевой безопасности, VOL.7, № 12, декабрь 2007 г.
, стр.
54-65 [2] Кнут, Д.
?.
, Искусство компьютерного программирования, Vol. Глава 3: Сортировка и поиск, Эддисон Везели (переиздание Pearson Education), 2000 г.
[3] Фанг К.
Т.
, Ли Р.
и Суджианто А.
Планирование и моделирование компьютерных экспериментов.
Чепмен и Холл, 2006 г.
[4] С.
Чакраборти, С.
, Моди, Д.
Н.
и Паниграхи, С.
, Будут ли статистические границы, основанные на весе Революционировать в ИТ?, Международный журнал вычислительного познания, Vol. 7(3), 2009, 16-22 [5] Чакраборти, С.
и Сураб, С.
К.
, Подход, ориентированный на компьютерный эксперимент, Алгоритмическая сложность, Lambert Academic Publishing, 2010 г.
[6] Чакраборти, С.
Обзор книги «Проектирование и моделирование компьютерных экспериментов», автор: К.
Т.
Фанг, Р.
Ли и А.
Суджианто, Чепмен и Холл, 2006 г.
, опубликовано в журнале Computing Reviews, 12 февраля 2008 г.
, www.reviews.com/widgets/reviewer.cfmЭreviewer_id=123180&count=26 [7] Кеннеди В.
и Джентл Дж.
Статистические вычисления, Marcel Dekker Inc., 1980. [8] Махмуд Х.
, Сортировка: теория распределения, John Wiley and Sons, 2000. [9] Сакс Дж.
, Уэлч В.
, Митчел Т.
и Винн Х.
Планирование и анализ компьютерных экспериментов, Statistical Science 4 (4), 1989. [10] Сундарараджан К.
К.
и Чакраборти С.
Новый алгоритм сортировки // Прикладная математика.
и компьютер.
, Vol. 188(1), 2007, с.
1037-1041 Теги: #внутренняя сортировка #равномерное распределение #средняя временная сложность #статистический анализ #статистическая оценка #Алгоритмы

-
Как Мы Перевели Сервер На Php 7
19 Oct, 24 -
Коммуникатор Qigi I6
19 Oct, 24


