В продолжение статьи Евгения Ческидова.
Директ. Анализируем конкурентную среду» Я хочу показать, как с помощью не очень сложных расчетов и API Яндекса можно извлечь из Директа буквально всю информацию о рекламных кампаниях конкурентов.
Скажу сразу, что идея еще не проверена на практике, сам факт наличия всей информации и соответственно возможности этого расчета был показан Ческидовым только вчера, а алгоритм родился буквально сейчас .
Но математически все сходится.
Будьте внимательны, под катом очень много формул.
1. Сначала введем обозначения:
я – это порядковый номер объявления на странице «показать все результаты рекламы».б [i] = ставка, неизвестная на данный момент максимальная ставка для i-го объявления.
Из правил Директа следует, что 20 ≥ b[1] ≥ b[2] ≥ b[3] ≥…≥ b[i] ≥ b[i+1] ≥… ≥ 0,01 (1) с [i] – CTR i-го объявления нам пока неизвестен, 0,01 ≤ c[i] ≤ 1,0 а [i] — «эффективная ставка», по которой сортируются объявления в поисковой выдаче по определению.
а[i] = b[i] ∙ c[i] (2) о [i] – позиция i-го объявления в поисковой выдаче (странице результатов поиска).
Порядок в результатах поиска определяется a, а не b, поэтому обычно o[i] ≠ i. Этот факт подробно рассмотрен в статье Ческидова.
р [j] — обратная функция к o[i], то есть r[o[i]] = o[r[i]] = i. Физически это индекс i объявления, занимающего j-ю позицию в поисковой выдаче, если предположить, что в спецразмещении есть объявления с номерами j = 1.3, а в правом блоке - с номерами.
j = 4.10. Из правил конкуренции для прямой рекламы в поисковой выдаче мы знаем, что a[r[1]] ≥ a[r[2]] ≥ … ≥ a[r[j]] ≥ a[r[j+1]] ≥ … (3) с [i] — номер стратегии показа по похожим ключевым словам, выбранной для i-го объявления: • s[i] = 0, если в качестве ключевой используется фраза без кавычек и отрицательных слов • s[i] = 1, если используется ключевое слово с минус-словами.
• s[i] = 2, если используется ключевое слово в кавычках Случай s[i]=2 можно определить, заметив отсутствие рекламы ключевой фразы с несуществующим словом, например, [розовые слоны fv243ae].
Чтобы определить случай s[i]=1, нужно найти наиболее очевидное (частотное) минус-слово для запроса в Wordstat и проверить наличие объявления по запросу с этим минус-словом, например [розовые слоны для бесплатно].
Из «прогноза бюджета» для каждой стратегии s можно извлечь средние значения начальных условий b0, c0 и, соответственно, a0: b0[s,1] – прогноз цены первого места в спецпроживании b0[s,3] – прогноз стоимости входа в специальное размещение c0[s,3] — прогноз CTR в спецразмещении b0[s,4] – прогноз цены первого места c0[s,4] – прогноз CTR первого места b0[s,10] – прогноз цены входа для гарантированных показов c0[s,10] — прогноз CTR в гарантированных показах.
Еще раз отметим, что это средние прогнозы, а не реальные значения параметров, т.е.
b0[s,i] ≠ b[i] для всех i > 1 Но можно утверждать, что эффективная ставка a[i] в прогнозе в точности равна реальной эффективной ставке i-го места, то есть a0[s[i],i]=a[r[i]], а точнее а0[s[3],3] = а[r[3]] (4) а0[s[4],4] = а[r[4]] (5) а0[s[10],10] = а[r[10]] (6) Наконец, обозначим через К [s] общее количество поисков в месяц по ключевому слову для каждой стратегии.
2. Статистическая модель пользователя Яндекса
Как человек просматривает страницу результатов? Читает первое объявление, с некоторой вероятностью п нажимает на него, в противном случае читает второе объявление, с некоторой вероятностью нажимает еще раз и так далее.
Переведем это на язык формул и обозначим Xi дискретное событие, равное 1, если пользователь кликнул по i-му объявлению, и 0, если он не кликнул: 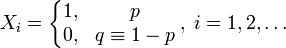
Поскольку результаты поиска просматривают тысячи пользователей, такие события независимы.
Математики доказали, что в такой модели вероятность нажатия на i-ю позицию подчиняется закон геометрического распределения и равен п (п) = р ∙ (1-р) н , (7) где n — номер объявления, начиная с нуля, и п – это определенный параметр, который зависит от конкретной ключевой фразы.
Сама по себе функция P(n) еще не является CTR, поскольку учитывает только положение объявления на странице.
В Директе на CTR также влияет выборка, используемая для показа конкретного объявления (то есть стратегия показа), история позиций (накопленный CTR) и качество самого объявления.
Историю можно накопить, методично сканируя результаты поиска.
Что касается качества самой рекламы, то в конкурентных тематиках оно примерно одинаковое, а поскольку пользователи не читают результаты поиска, а просматривают их по диагонали, то это не играет большой роли.
Если перевести с математического на русский, то объявление на 8 позиции не может иметь CTR 70% или хотя бы 20%.
И наоборот, вы, конечно, можете разместить отвратительное объявление на первом месте спецразмещения и «давить деньги», но, независимо от вашего бюджета, по мере сбора статистики от пользователей CTR этого объявления будет падать и ты неизбежно упадешь сначала с первого места, а потом и с выступлений вообще.
Поэтому в этой статье для простоты я буду рассматривать CTR как функцию позиции и стратегии.
Заинтересованные читатели могут учитывать такие факторы, как история рейтинга, включение ключевого слова в текст объявления или релевантность текста объявления другим объявлениям на странице.
Следует отметить, что между теорией и практикой все еще существует небольшое неустранимое расхождение: в математике последовательность предполагается бесконечной, но реальный результат ограничен.
В результате реальный CTR последних объявлений в блоке оказывается немного выше теоретической вероятности.
Чтобы было хоть немного понятнее о чем шла речь в предыдущих пунктах, приведу два графика:
На первом изображен график зависимости CTR от позиции с доклад Александра Садовского : 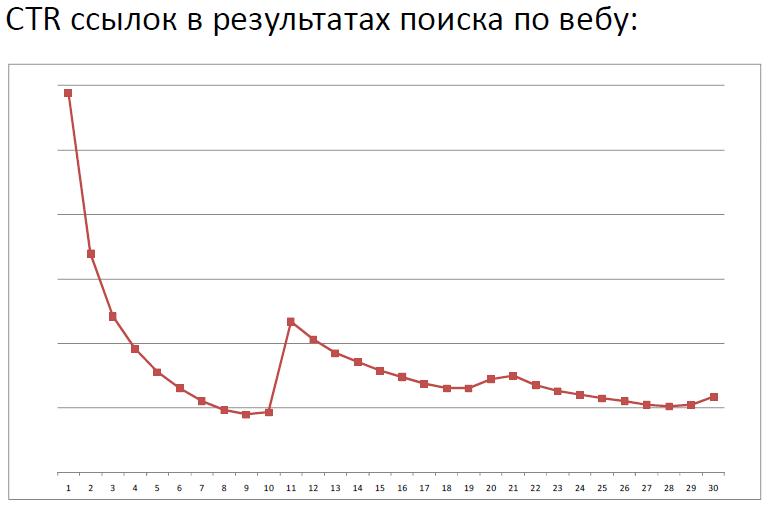
На втором графике показана функция вероятности для геометрического распределения с разными параметрами p (из Википедии).
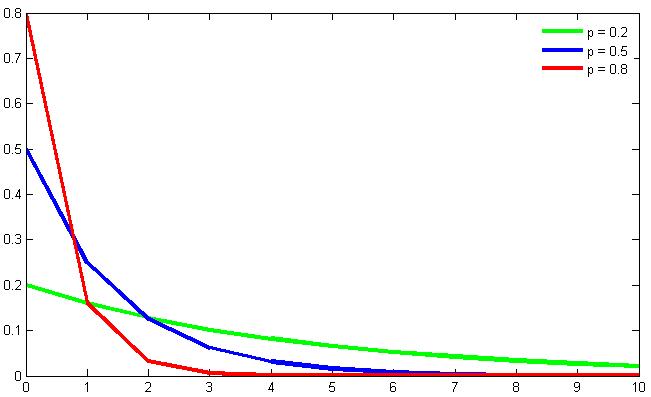
3. Расчет теоретического CTR
Зная его позицию и стратегию для каждого объявления, нам необходимо оценить ожидаемый CTR этого объявления, то есть вычислить параметр p по формуле (7).Для правого блока все просто, ожидаемый CTR первого места в правом блоке нам дает Яндекс, то есть пр[s] = c0[s,4] (8) который необходимо рассчитать для всех стратегий s. Зная pr, мы можем рассчитать теоретические значения c1 для всех i по формуле с1[s,r[i]] = pr[s] ∙ (1 – pr[s]) р[и]-4 (9) Для верхнего блока (там другой параметр p) все немного сложнее, поскольку Яндекс раскрывает значение CTR не для первого объявления в специальном размещении, а только для третьего.
Вам придется поискать справочник по математике и решить кубическое уравнение.
п 3 – 2р 2 + p – c0[s,3] = 0 (10)
Далее, аналогично (8), только показатель степени будет r[i]-1.
4. Собираем систему уравнений.
Запишем выражения (1) и (3) в виде системы обыкновенных неравенств б[1] ≥ б[2] б[2] ≥ б[3] … б[9] ≥ б[10] b[r[1]] ∙ c[r[1]] ≥ b[r[2]] ∙ c[r[2]] b[r[2]] ∙ c[r[2]] ≥ b[r[3]] ∙ c[r[3]] … б[r[9]] ∙ c[r[9]] ≥ b[r[9]] ∙ c[r[9]] (для случая N=10 объявлений) Примечание: мы не сможем решить систему, если объявлений будет больше 10 — мы просто не увидим «вторую страницу директа» и не будем знать связь между a[r[i]] для i> 10. Постороннюю рекламу придется исключить из расчетов.
Добавим в систему граничные условия на b и c и начальные значения, заданные уравнениями (4).
(6).
Таким образом, мы получаем систему неравенств второго порядка с 2N неизвестными, 3N неравенствами и тремя уравнениями.
Свойство этой системы таково, что для каждой пары неизвестных b[i], c[i] существует небольшая гиперболическая область, в которой эти параметры могут изменяться без нарушения условий неравенств.
Чтобы устранить эту неопределенность, нам нужно добавить дополнительные ограничения на b и c, чтобы b[i] стремилось к нулю, если позиции сохраняются (никто не будет переплачивать просто так), а c[i] стремилось к теоретически ожидаемым значениям.
С этими дополнительными ограничениями мы не сможем найти реальное значение максимальных ставок, а только минимально необходимые значения для того, чтобы объявления заняли наблюдаемые позиции.
На практике это означает, что если самое дорогое объявление имеет ставку 10 USD, а на самом деле для первого места нужно всего 3,01 USD, мы найдем значение 3,01. Но в нашем случае это не имеет значения, потому что Яндекс уже сообщает нам максимальную ставку по ключевому слову, а все остальные ставки стабильно ниже предыдущей.
Введем в систему «функцию штрафа» — меру, показывающую, насколько приближенное решение не удовлетворяет нашим условиям.
Структура штрафной функции будет примерно такой: 1. Большой штраф за невыполнение неравенств (1) (порядок b[i]), малый штраф за «перевыполнение» этих неравенств; 2. Большой штраф за невыполнение неравенств (2) (порядок a[i]), нулевой штраф за их выполнение.
3. Очень большой штраф за несоблюдение граничных условий на c[i] 4. Большой штраф за невыполнение уравнений (4).
(6).
5. Некоторый штраф за отклонение c[i]-х от теоретических значений.
Таким образом, мы получаем обычную задачу оптимизации штрафной функции, то есть нахождение таких значений b[i] и c[i], при которых значение штрафной функции будет минимальным.
Алгоритмы поиска такого решения давно известны из раздела математики, называемого «методами оптимизации».
Применив подходящий алгоритм, мы в конечном итоге получим значения b[i] и c[i], то есть ставки и CTR для всех конкурирующих объявлений.
5. ПРИБЫЛЬ!
Теперь самое интересное: зная ставку, CTR, стратегию и количество показов K[s] для каждого объявления, мы можем оценить максимальный ежемесячный бюджет для каждого объявления по заданному ключевому слову.Зная CTR и K[s] – оцените количество переходов и, следовательно, целевого трафика на сайте конкурента.
А зная бюджет и количество переходов, мы можем оценить стоимость каждого перехода, то есть качество настройки рекламной кампании.
Зная качество рекламной кампании, мы можем сделать далеко идущие выводы, которые, однако, невозможно описать никакой математикой) Наконец, зная семантическое ядро предметной области и подключившись к Директу через API, мы можем практически в автоматическом режиме рассчитать общий бюджет всех рекламных кампаний конкурентов по всему ядру.
«Почти» — потому что основные и минус-слова все равно придется подбирать вручную.
А зная реальные бюджеты всех конкурентов.
ну вы поняли.
В общем, Яндекс предоставил всю информацию для игры в Директ «с открытыми глазами».
Вот что представляет собой прикладной анализ данных в действии.
Теги: #Яндекс.
Директ #Яндекс.
директ #математика #математика
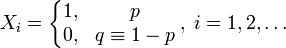
-
Изучаем Английский С Анки
19 Oct, 24 -
Широкие Полномочия Фсб
19 Oct, 24


