Исследование Устойчивости Сверточных Нейронных Сетей. Часть 1: Теория

Если вам интересно понять, насколько стабильны современные (в первую очередь сверточные) нейронные сети, насколько легко изменить их выходные данные, слегка исказив входные данные, и можно ли это сделать на уровне реальных (физических) атрибутов объекты перед съемкой их (фото)видеокамерой - Добро пожаловать под кат!

Введение в сверточные нейронные сети

• Более объемный (содержал больше параметров),
• Глубже (содержал больше расчетных блоков),
• Лучше! (более правильно решали поставленные перед ними задачи)

1. Как в настоящее время сравниваются качество человеческого распознавания и CNN в известных базах данных?
2. Насколько устойчивы CNN к своим входным данным? Легко ли их сломать?

Прогресс в сверточных нейронных сетях

Примеры изображений ImageNet :



ЛФВ :



Итак, классификация на ImageNet:

• Ошибка Топ-5 (вероятность того, что правильный класс не окажется в пятёрке, скорее всего) для человека: 5.1% ( доказательство в блоге Карпат )
• Топ-5 ошибок в социальных сетях: 2.0% (по крайней мере, на конец прошлого года; сейчас уж точно приближаются к проценту, а то и меньше.

  В любом случае для заказа можно обратиться к статье" Исправление несоответствия разрешения поездного теста ")

• Ошибка проверки для человека: 2.47% (см.

  доказательство в статье " Классификаторы атрибутов и изображений для проверки лица ")

• Ошибка проверки для SNA: 0.17% (классическая работа по распознаванию лиц - " Arcface: дополнительная потеря углового поля для глубокого распознавания лиц.

  ")

(Не)стабильность сверточных нейронных сетей

Для ответа на второй вопрос обратимся к работам исследователей, стоящих у истоков тестирования СНС на устойчивость.

Оказывается, во входные данные можно внести практически незаметные для человеческого глаза возмущения, которые, тем не менее, полностью изменяют выходные данные нейронной сети.

Например, результат классификации с " панды "изменения в" гиббон "при внесении крайне незаметных возмущений: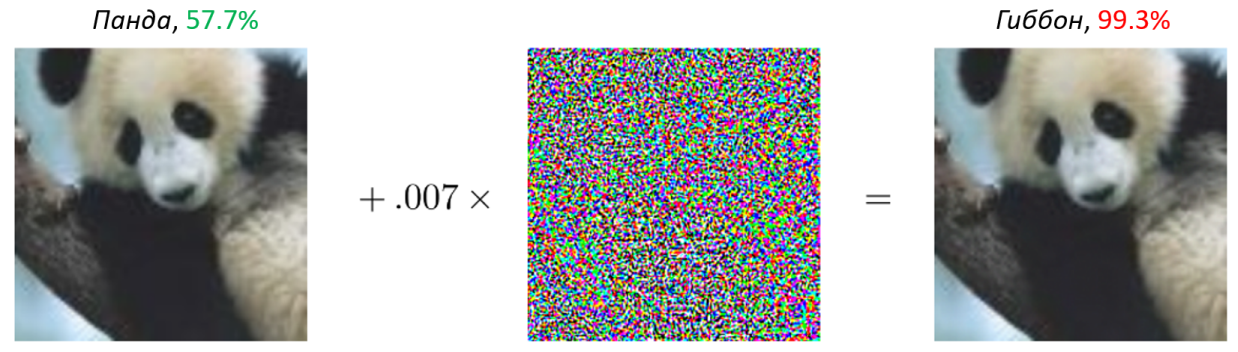



Изображение предоставлено arxiv.org/pdf/1412.6572.pdf Итак, такие почти незаметные возмущения, изменяющие выходные данные нейронной сети, называются состязательные примеры (или, часто, нападения к этой самой нейронной сети); устойчивое выражение на английском языке состязательные примеры/атака .

Может показаться, ну, возможно, такие состязательные примеры существуют только для классификационных сетей (ну и переведите там класс из правильного в неправильный).

Однако мы быстро выяснили, что аналогичные проблемы наблюдаются и в сетях, обнаруживающих объекты (обведены прямоугольником), и даже в сетях сегментации (которые присваивают класс каждому пикселю изображения): например, вы можете увидеть работу " Состязательные примеры семантической сегментации и обнаружения объектов ".

И наконец, предвидя возражения в виде «ну это все картинки, в нашем замечательном НЛП такого не бывает!» [НЛП = Обработка естественного языка], можно привести отличный пример из статьи " Состязательные примеры оценки систем понимания прочитанного ", что относится прежде всего к так называемым вопросно-ответным системам, в которых изучаемой системе дается небольшой фрагмент текста (несколько предложений), а затем задается простой вопрос для понимания этого фрагмента.

Вот оригинальный текст:

Пейтон Мэннинг стал первым защитником, когда-либо приведшим две разные команды к нескольким Суперкубкам.

Он также является самым старым защитником, когда-либо игравшим в Суперкубке в возрасте 39 лет. Предыдущий рекорд принадлежал Джону Элвею, который привел Бронкос к победе в Суперкубке XXXIII в возрасте 38 лет и в настоящее время является исполнительным вице-президентом Денвера по футбольным операциям и футбольным операциям.

Главный управляющий.

Как звали квотербека, которому было 38 лет в Суперкубке XXXIII?

Если в качестве последнего предложения к тексту добавить вот этот кусок, совершенно не связанный с вопросом:

Защитник Джефф Дин имел футболку под номером 37 в Champ Bowl XXXIV.

Откуда берётся нестабильность и как с ней бороться?

Давайте сосредоточимся на одном (и, возможно, наиболее легко интерпретируемом), а именно: недостаточная обобщающая способность нейронных сетей .

Из-за этого границы классификации, которые строятся при обучении нейронной сети, часто проходят очень близко к обучающим данным, а иногда легко «перешагнуть» с помощью минимального возмущения из области, соответствующей одному классу, в область соответствующий другому классу: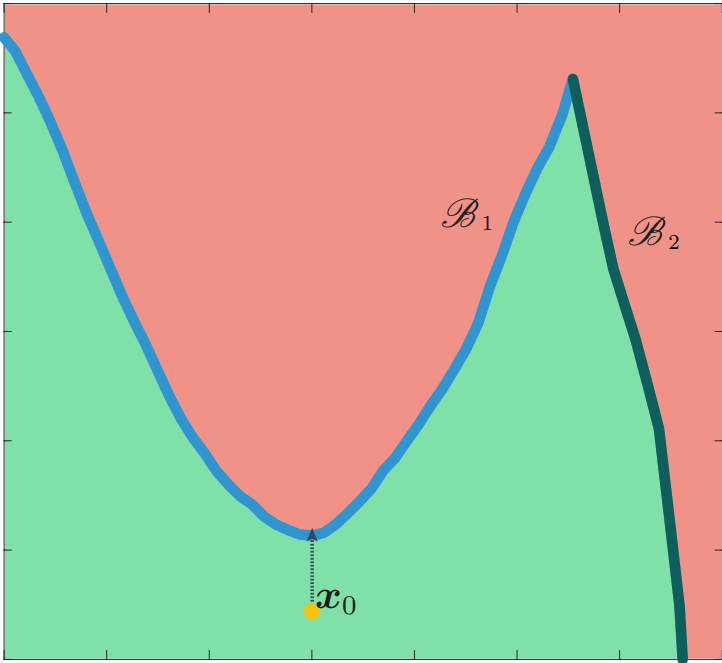



Изображение предоставлено arxiv.org/pdf/1608.08967.pdf Примечание на полях : по сути техника дополнения входные данные при обучении (добавляя к исходным данным слегка преобразованные их версии: например, с помощью вращения, затемнения/осветления, масштабирования и т. д.) и пытаясь в какой-то степени решить эту проблему – отодвигая границу, хотя и только в некоторых направления (которые соответствуют выбранным увеличениям).

При этом направления с очень близкими границами все еще остаются.

Итак, мы знаем, что CNN можно обмануть небольшим искажением пикселей.

Почему бы при обучении не добавить для каждого обучающего примера всю его попиксельную окрестность (по какой-то норме, например,



[о нормах чуть позже]).

Ниже замечательная иллюстрация из статьи " К моделям глубокого обучения, устойчивым к состязательным атакам ", где звездочками отмечены окрестности пикселей обучающих примеров, которые при начальной разделительной линии попали в область соседнего класса - следовательно, разделяющую кривую нужно преобразовать так, чтобы эти звездочки попали в область своего класса: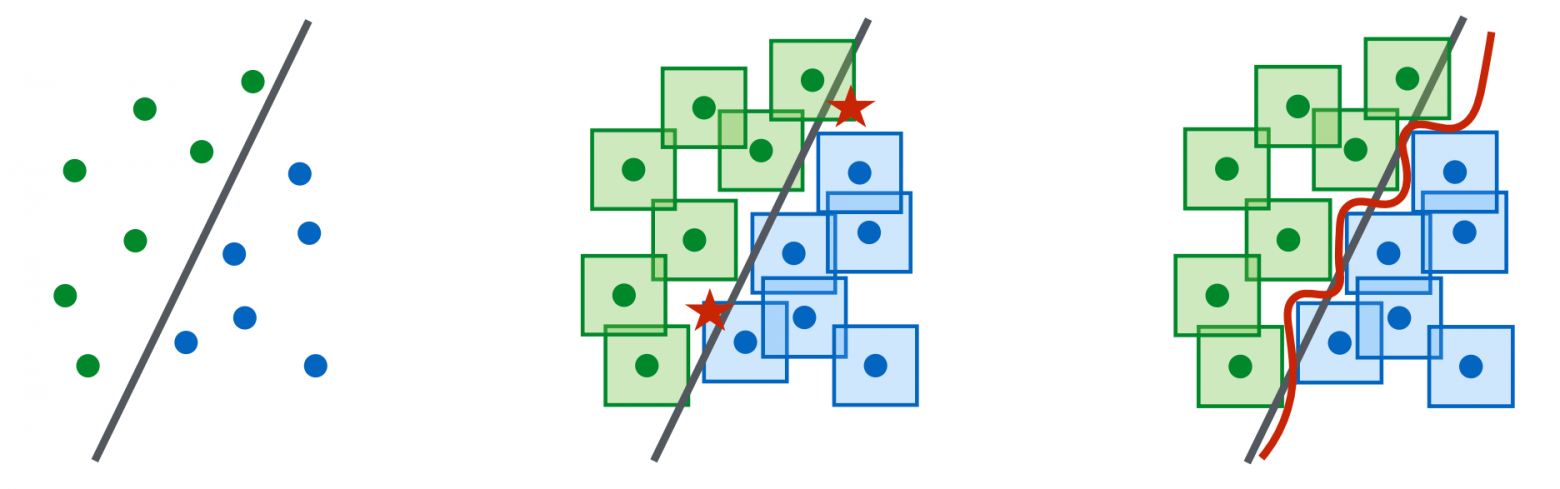



Ну, сказано и сделано.

Давайте проведем необходимые расчеты на коленях.

При условии, что:

• изображение оригинального размера
  
  
  
  пикселей, 3 цвета RGB,
• наш глаз мало различает колебания цвета пикселей в 2-х градациях (из 256): в каждой точке для каждого цвета мы можем допустить
  
  
  
  значение,

, что полностью разрушает идею коррекции стабильности СНС простым методом «в лоб».

Как видите, простое перечисление окрестностей пикселей — трудоемкая задача.

Но нам не нужна та окрестность перспективного примера, которая уже находится в правильной области классификации! Наоборот, необходимо учитывать те точки из окрестности, которые попадают не в ту область для классификации (по сути, своего рода хард-майнинг обучающих примеров).

И этот метод обучения с использованием дополнительных, наиболее сложных примеров из окружающей области, называется состязательное обучение ( состязательная подготовка ).

По вопросам материальной части вы можете обратиться к первоисточнику о состязательном обучении для CNN. Примечание плюсы состязательное обучение.

Таким образом, больше не нужно перебирать огромное и подавляющее количество точек из окрестности, а достаточно просто взять самые сложные.

Правда, как именно решать эти «самые сложные» вопросы — вопрос хороший, да и фактически до сих пор открытый.

Обычно используется некоторый метод генерации состязательных примеров и таким образом получить после обучения модель, защищенную от этого метода генерации.

Минусы также вполне очевидны.

Во-первых, купив защиту от никто метода генерации атаки, используемого в обучении, мы не можем ничего гарантировать в отношении любого другой метод генерации состязательных примеров.

А еще любой метод генерации таких примеров добавляет приличный объем накладных расходов (обычно гораздо больше, чем обычный шаг градиента с использованием метода обратного распространения ошибки).

Обозначения: формальная часть

• Позволять
  
  
  
  - входное изображение
  
  
  
  , Где
  
  
  
  — количество цветов (1 для черно-белого, 3 для цветного в формате RGB),
  
  
  
  — пространственные размеры (ширина, высота);
• 
  
  
  
  - правильный класс входа
  
  
  
  ;
• 
  
  
  
  — параметры классификатора CNN;
• 
  
  
  
  — функция потерь;
• 
  
  
  
  — вывод классификатора (распознанный класс); мы стремимся к равенству в образовании
  
  
  
  ;
• 
  
  
  
  — добавка добавка к входу
  
  
  
  ;

1. 
   
   
   
   (мы изначально правильно определяем класс),
2. 
   
   
   
   («разрушение» CNN с помощью возмущения r),
3. 
   
   
   
   (мы остаемся в множестве допустимых значений).

Аналогичным образом можно определить такое понятие, как стабильность классификатора — найти такой класс возмущения



, в котором классификатор не меняет свой вывод:



.

В обозначениях выше регулярное обучение CNN на примерах можно сформулировать как минимизацию следующего ожидания:



В состязательное обучение сначала генерируем (например, каким-либо методом атаки) наиболее сложный пример из некоторой окрестности



пример ввода (например, по



-norm), и только потом минимизировать по параметрам нейросети:



стандарты l_p: напоминание Напомним наиболее часто используемые нормы



Для



:

• 
  
  
  
  :
  
  
  
  (обычная евклидова норма);
• 
  
  
  
  :
  
  
  
  (так называемая метрика городских кварталов);
• 
  
  
  
  :
  
  
  
  (максимальный модуль; именно на основе этой метрики человеческий глаз воспринимает визуальную информацию);
• 
  
  
  
  :
  
  
  
  (количество ненулевых значений).

Для



"норма"



, для которого



, это не норма .

Состязательные примеры в компьютерном зрении: история проблемы

Обманывающие изображения

И, скажем так (это не всегда так, но все же), на картинках, принадлежащих к этим классам, вероятности отображаются более или менее осмысленно (хотя есть, конечно, ошибки).

Но что произойдет, если мы введем изображение, не принадлежащее этим N классам, то есть, математически говоря, вне области определения? И хорошо, если на выходе будет равномерный вектор вида (1/N,.

,1/N) — типа сеть не понимает, что происходит. Гораздо хуже, когда по объекту вне области определения сеть выдаёт вполне определённый ответ — то есть одна из вероятностей будет значительно больше остальных.

Итак, изначально стабильность CNN изучалась с точки зрения адекватного реагирования на различные входные сигналы.

Оказалось, что существуют примеры (построенные на основе определенной структуры или являющиеся по сути белым шумом), которые на выходе CNN могут с большой вероятностью дать любой (в том числе заданный) класс.

Такие примеры назывались « обманчивые изображения (обманные изображения) и были построены с использованием эволюционных алгоритмов:



За подробностями любопытный читатель может обратиться к первоисточнику».

Глубокие нейронные сети легко обмануть: прогнозы с высокой достоверностью для неузнаваемых изображений ".

КЖПО

Поэтому практически сразу было предложено использовать линейную часть функции потерь в окрестности входного изображения.

и следуем градиенту (см.

источник " Объяснение и использование состязательных примеров "):



Где



– некая константа, отвечающая за скорость движения, а



- не тот класс, в сторону которого нас «подталкивают» (обманывают) смотреть СНС.

Этот метод назывался Ф Аст г сияющий С зажечь М метод (по-русски " быстрый метод, основанный на знаке градиента ", но это все равно звучит не очень хорошо), или FGSM. Напоминание : для оптимизации весов CNN используется метод обратного распространения ошибки, при котором берется градиент по весам CNN, т.е.

.

Итак, в этой работе мы изучаем норму возмущения



максимально приближен к тому, как работает человеческое зрение (восприятие визуальной информации).

И-ФГСМ (ПГД)

Для решения этой проблемы используется итерационный метод. я теративный КЖПО , или I-FGSM, что позволяет более точно продвигаться к границе классификатора.

Если



- проекция на



, Что



Более того, если мы хотим получить окончательное решение



"отошёл" от исходного примера



не более чем



по норме



и мы больше ничего не можем сделать



шагов, то можно сразу вывести эмпирическое правило скорости движения:



Примечание 1 .

Но в целом метод I-FGSM гораздо более известен как разработан метод градиентного спуска п прогнозируемый г сияющий Д эсцент, или ПГД, хотя это название появилось почти год спустя .

Заметка 2 .

В целом метод I-FGSM/PGD до сих пор наиболее широко используется на практике, поскольку он прост и достаточно стабилен (хотя и не так быстр, как простой FGSM).

МИ-ФГСМ

Поэтому в целом существует целая тенденция перетаскивания успешных поворотов градиентного спуска в состязательную зону, и наиболее удачным таким примером является использование момент .

Как следствие, работа» Усиление состязательных атак с импульсом «предлагает использовать сглаживание градиента в итеративном методе I-FGSM — М сальник Я-КОЖПО , или МИ-ФГСМ.

Ход работы следующий:



где g обозначает сглаженный градиент:



Ну и вот сравнительная таблица трех последних методов, из которой видно, что MI-FGSM использовать по-прежнему предпочтительнее (чем больше цифр, тем выше успешность атаки):

Один пиксель

Однако существуют методы (один из первых — JSMA , но это не очень практично и удобно), которые не учитывают максимальную разницу в яркости (по норме



), и максимальное количество пикселей, которое можно изменить (по норме



).

Эти типы состязательных примеров устраняют разрыв между цифровой и практической сферами (см.

практические состязательные примеры в следующем разделе), и наиболее крайним из них является атака по одному пикселю .

На работе" Атака одним пикселем для обмана глубоких нейронных сетей "рассмотрен предельный случай



-атаки.

Для этого авторы используют эволюционный алгоритм (а именно алгоритм дифференциальная эволюция ) для поиска состязательных примеров:

• Популяция состоит из 400 особей, каждая из которых задается пятью числами: двумя координатами и тремя цветовыми каналами;
• Поколение ребенка представляет собой линейную комбинацию трех случайных родителей.

, грузовик ):

Краткие выводы по первой части

• На данный момент CNN (в целом) работают намного лучше, чем люди;
• CNN легко «обмануть», используя нестабильность их входных данных;
• Наиболее распространенным ингредиентом для создания состязательного примера является градиент нейронной сети на входных данных.

Ссылки

• «Практическое» введение в тему состязательных атак читайте в 2019 году на сайте Фестиваль науки в Московском государственном университете.

  М.

  В.

  Ломоносова:

• Еще немного математики -

• Темные Истории: Эдгар Аллан По - Преждевременные Похороны

  19 Oct, 24

• Программное Обеспечение Для Управления Чпу

  19 Oct, 24

• Типы Видео В Интернете

  19 Oct, 24

• Павел Дуров Заявил О Появлении Платных Сервисов От Сторонних Разработчиков В Telegram

  19 Oct, 24

• Беспилотные Автомобили Учатся Читать Язык Тела Людей На Улицах

  19 Oct, 24

• Биологические Эффекты Длительного Космического Полета

  19 Oct, 24

• На Одну Виртуальную Сеть Станет Меньше!

  19 Oct, 24

• 11.11: Шпаргалка По Флэш-Продажам

  19 Oct, 24

• T-Mobile Рейк Для G1

  19 Oct, 24

• Школьные Дневники Теперь В Сети

  19 Oct, 24