Использование Qml Map Для Построения Авиамаршрутов. Часть 1.

Я использую QML для построения графических интерфейсов довольно давно, но возможность работать в реальном проекте с API местоположения Qt и QML Map до сих пор не было.

Поэтому стало интересно попробовать этот компонент для построения авиамаршрутов.

Под катом описание реализации редактора для создания подобных траекторий на карте: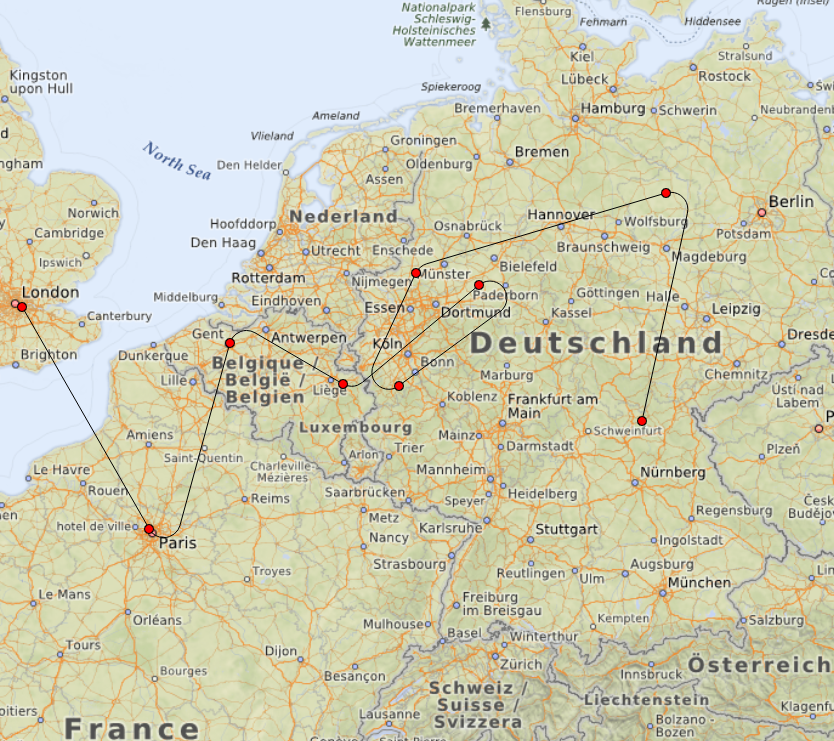

Использование QML Map для построения авиамаршрутов.

Часть 1.

Для упрощения реализации наши самолеты летают в 2D-плоскости на одной высоте.

Скорость и допустимая перегрузка фиксированы - 920 км/ч и 3g, что дает радиус поворота.

Использование QML Map для построения авиамаршрутов.

Часть 1.

Траектория состоит из сегментов следующего типа: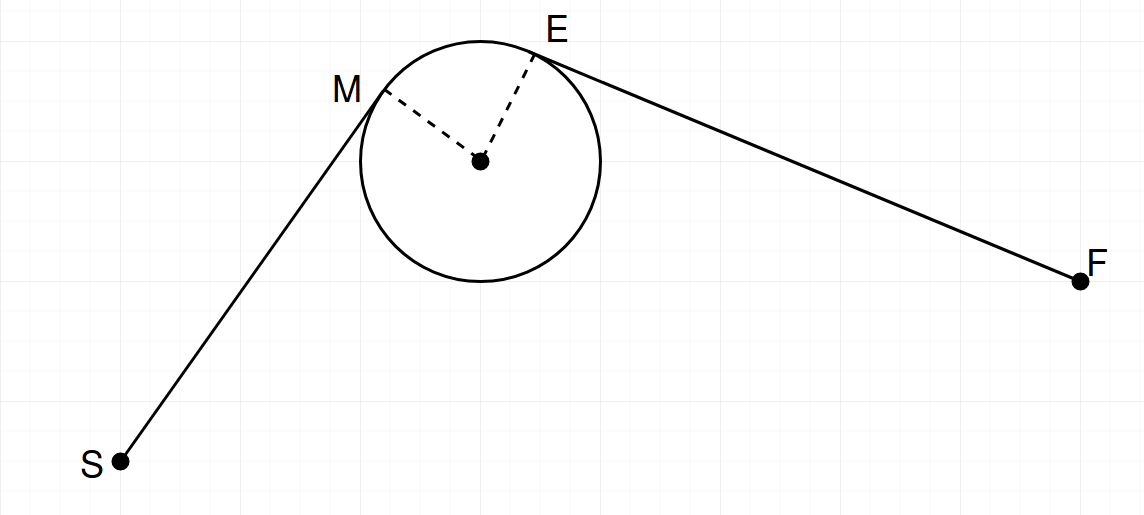

где S – начало маневра (оно же точка выхода из предыдущего), М – начало поворота, Е – выход из него, F – конечная точка (М для следующего).

Для расчета точек входа и выхода траектории я использовал уравнение касательной к окружности, расчеты оказались довольно громоздкими, уверен, можно сделать и проще.

   

 void Manoeuvre::calculate()
 {
     // General equation of line between first and middle points
     auto A = mStart.y() - mMiddle.y();
     auto B = mMiddle.x() - mStart.x();
 
     // Check cross product sign whether final point lies on left side
     auto crossProduct = (B*(mFinal.y() - mStart.y()) + A*(mFinal.x() - mStart.x()));
 
     // All three points lie on the same line
     if (isEqualToZero(crossProduct)) {
         mIsValid = true;
         mCircle = mExit = mMiddle;
         return;
     }
 
     mIsLeftTurn = crossProduct > 0;
     auto lineNorm = A*A + B*B;
     auto exitSign = mIsLeftTurn ? 1 : -1;
     auto projection = exitSign*mRadius * qSqrt(lineNorm);
 
     // Center lies on perpendicular to middle point
     if (!isEqualToZero(A) && !isEqualToZero(B)) {
         auto C = -B*mStart.y() - A*mStart.x();
         auto right = (projection - C)/A - (mMiddle.x()*lineNorm + A*C) / (B*B);
         mCircle.ry() = right / (A/B + B/A);
         mCircle.rx() = (projection - B*mCircle.y() - C) / A;
     } else {
         // Entering line is perpendicular to either x- or y-axis
         auto deltaY = isEqualToZero(A) ? 0 : exitSign*mRadius;
         auto deltaX = isEqualToZero(B) ? 0 : exitSign*mRadius;
         mCircle.ry() = mMiddle.y() + deltaY;
         mCircle.rx() = mMiddle.x() + deltaX;
     }
 
     // Check if final point is outside manouevre circle
     auto circleDiffX = mFinal.x() - mCircle.x();
     auto circleDiffY = mFinal.y() - mCircle.y();
     auto distance = qSqrt(circleDiffX*circleDiffX + circleDiffY*circleDiffY);
 
     mIsValid = distance > mRadius;
 
     // Does not make sence to calculate futher
     if (!mIsValid)
         return;
 
     // Length of hypotenuse from final point to exit point
     auto beta = qAtan2(mCircle.y() - mFinal.y(), mCircle.x() - mFinal.x());
     auto alpha = qAsin(mRadius / distance);
     auto length = qSqrt(distance*distance - mRadius*mRadius);
 
     // Depends on position of final point find exit point
     mExit.rx() = mFinal.x() + length*qCos(beta + exitSign*alpha);
     mExit.ry() = mFinal.y() + length*qSin(beta + exitSign*alpha);
 
     // Finally calculate start/span angles
     auto startAngle = qAtan2(mCircle.y() - mMiddle.y(), mMiddle.x() - mCircle.x());
     auto endAngle = qAtan2(mCircle.y() - mExit.y(), mExit.x() - mCircle.x());
     
     mStartAngle = startAngle < 0 ? startAngle + 2*M_PI : startAngle;
     endAngle = endAngle < 0 ? endAngle + 2*M_PI : endAngle;
 
     auto smallSpan = qFabs(endAngle - mStartAngle);
     auto bigSpan = 2*M_PI - qFabs(mStartAngle - endAngle);
     bool isZeroCrossed = mStartAngle > endAngle;
 
     if (!mIsLeftTurn) {
         mSpanAngle = isZeroCrossed ? bigSpan : smallSpan;
     } else {
         mSpanAngle = isZeroCrossed ? smallSpan : bigSpan;
     }
 }

Завершив расчет математической модели нашей траектории, приступим непосредственно к работе с картой.

Естественным выбором для построения полилиний на карте QML является добавление КартаПолилиния прямо на карту.

Map { id: map plugin: Plugin { name: "osm" } MapPolyline { path: [ { latitude: -27, longitude: 153.0 }, .

] } }

Изначально я хотел предоставить пользователю возможность моделировать каждый последующий участок маршрута «на лету» — создать эффект движения траектории за курсором.

Использование QML Map для построения авиамаршрутов.

Часть 1.

Изменять путь при перемещении курсора это достаточно затратная операция, поэтому я попробовал использовать предварительные «пиксельные» траектории, которые отображаются до тех пор, пока пользователь окончательно не сохранит маршрут.

Repeater { id: trajectoryView model: flightRegistry.hasActiveFlight ? flightRegistry.flightModel : [] FlightItem { anchors.fill: parent startPoint: start endPoint: end manoeuvreRect: rect manoeuvreStartAngle: startAngle manoeuvreSpanAngle: spanAngle isVirtualLink: isVirtual } }

FlightItem является QQuickItem -ох, ах QAbstractListModel модель полета позволяет обновлять необходимые участки траектории при изменении данных для маневра.

QVariant FlightModel::data(const QModelIndex &index, int role) const { if (!index.isValid()) { return QVariant(); } switch (role) { case FlightRoles::StartPoint: return mFlight->flightSegment(index.row()).

line().

p1(); case FlightRoles::EndPoint: return mFlight->flightSegment(index.row()).

line().

p2(); .

}

Это оперативное обновление позволяет предупреждать пользователя о невозможных маневрах.

Использование QML Map для построения авиамаршрутов.

Часть 1.

Только после завершения создания воздушного маршрута (например, щелчком правой кнопки мыши) маршрут будет окончательно добавлен на QML-карту в виде GeoPath с возможностью геопривязки (до этого момента нельзя перемещать или масштабировать карту, пиксели ничего не знают о долготе и широте).

Чтобы преобразовать сегмент пикселя в сегмент геокоординат, нам сначала нужно использовать систему координат, локальную относительно точки входа маневра (нашей точки S) для каждого маневра.

QPointF FlightGeoRoute::toPlaneCoordinate(const QGeoCoordinate &origin, const QGeoCoordinate &point) { auto distance = origin.distanceTo(point); auto azimuth = origin.azimuthTo(point); auto x = qSin(qDegreesToRadians(azimuth)) * distance; auto y = qCos(qDegreesToRadians(azimuth)) * distance; return QPointF(x, y); }

После того, как мы пересчитаем маневр в метры, необходимо выполнить обратную операцию и, зная географическую привязку точки S, перевести метры в широту-долготу.

QGeoCoordinate FlightGeoRoute::toGeoCoordinate(const QGeoCoordinate &origin, const QPointF &point) { auto distance = qSqrt(point.x()*point.x() + point.y()*point.y()); auto radianAngle = qAtan2(point.x(), point.y()); auto azimuth = qRadiansToDegrees(radianAngle < 0 ? radianAngle + 2*M_PI : radianAngle); return origin.atDistanceAndAzimuth(distance, azimuth); }

С формальной точки зрения, конечно, мы не можем считать нашу «пиксельную» и «метровую» траекторию идентичной, но возможность заглянуть в будущее и показать пользователю, что произойдет (или не произойдет, если самолет так не летает) мне показался очень вкусным.

он щелкнет в следующий раз.

После доработки траектории (она немного отличается от пиксельной по цвету и прозрачности, так как даже статические ломаные линии выглядят на карте не очень гладко).

Использование QML Map для построения авиамаршрутов.

Часть 1.

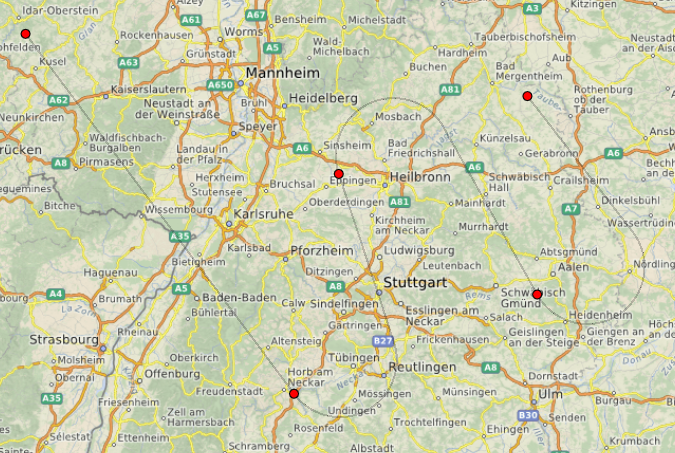
Доступные источники здесь , для компиляции я использовал Qt 5.11.2. В следующей части мы научим наш редактор перемещать контрольные точки траектории, а также сохранять/открывать существующие треки для последующей симуляции движения самолета.