Привет, Хабр! В самом конце года у нас есть время поделиться с вами новостью о том, что мы начинаем работу над «Байесовской статистикой: веселый путь» от издательства No Starch Press. Предлагаем перевод подробного интервью с автором книги; текст касается как самой книги, так и смежных тем и даже дополнительного чтения.

Меня, как и большинство разработчиков, интересуют многие вещи: функциональное программирование, операционные системы, системы типов, распределенные системы и наука о данных.
Вот почему я был так рад это услышать Уилл Курт , автор книги Научитесь программированию на Haskell написал книгу по байесовской статистике, опубликованную издательством No Starch Press. Людей, которые пишут книги на разные темы, не так много.
Я уверен, что Уиллу есть чем поделиться с читателями в своей новой книге – и я в ней не разочаровался.
Книга представляет собой отличный вводный материал, особенно для тех, у кого возникли проблемы со строгой математикой, но все же хочется чего-то добиться в области Data Science. Я рекомендую прочитать новую книгу Курта после Think Stats, но перед вероятностным программированием на Python: байесовский вывод и алгоритмы, байесовский анализ с помощью Python и выполнение байесовского анализа данных.
1. Зачем нам нужна еще одна книга по статистике? Почти все книги по байесовской статистике, доступные в настоящее время, предполагают, что читатель уже имеет общее представление о статистике или прочную основу в программировании.
Поэтому байесовская статистика сейчас часто воспринимается как продвинутая альтернатива классической (т. е.
частотной) статистике.
Таким образом, хотя популярность байесовской статистики растет, материалы по ней ориентированы в первую очередь на людей, уже имеющих хорошую количественную подготовку.
Когда человек решает просто «выучить статистику», он берет в руки вводную книгу, в которой рассказывается о статистике с точки зрения частоты, заканчивает ее, пройдя половину кучи тестов и правил, и чувствует, что вся тема очень запутанная.
Я хотел написать книгу по байесовской статистике, которую каждый мог бы взять, прочитать и уйти с интуитивным пониманием того, что значит статистически мыслить и как решать реальные проблемы с помощью статистики.
Я не вижу причин, по которым байесовская статистика не должна стать первым введением в эту тему для новичка.
Я был бы очень рад, если бы когда-нибудь люди, используя слово «статистика», начали иметь в виду байесовскую статистику, а частотная статистика превратилась бы в еще одну академическую нишу.
Для этого нужно больше книг, в которых введение в статистику для широкого круга читателей предлагалось бы именно с использованием байесовских методов, и автор учел, что это может быть самое первое знакомство читателя со статистикой.
Я сразу подумал назвать эту книгу «Статистика – это весело», но решил, что, вероятно, получу массу писем с ненавистью от людей, которые купили подобную книгу, чтобы подготовиться к вступительному экзамену по статистике, и обнаружили, что речь идет о чем-то.
полностью отличается! Я надеюсь, что моя книга станет маленьким шагом к тому времени, когда на вступительных экзаменах будут задавать байесовскую статистику, и чтение такой книги будет целесообразно даже тем, кто только готовится к экзамену.
2. Какова целевая аудитория книги? Может ли это прочитать человек без математического образования? При написании «Байесовская статистика прекрасна» я стремился создать книгу, которая в принципе была бы понятна каждому, кто освоил математику в средней школе.
Даже если вы лишь смутно помните алгебру, чтение книги ведется в том темпе, за которым вы сможете идти в ногу.
Байесовская статистика требует очень небольшого математического анализа и тем более упрощается при небольшой поддержке программного обеспечения, поэтому я добавил к книге два приложения, в которых излагаются основы языка R. Этого материала достаточно, чтобы R мог служить для вас продвинутым калькулятором, а основные идеи математического анализа представлены в таком объёме, что вы сможете понять все примеры в этой книге, где обсуждаются интегралы.
Однако обещаю, что для прочтения книги вам не придется решать какие-либо задачи из области математического анализа.
Более того, сколько бы я ни трудился, стараясь максимально свести к минимуму тот объем математических знаний, который необходим для прочтения книги, читая ее, вы постепенно начнете усваивать математический образ мышления.
Если вы действительно разбираетесь в математике, которой занимаетесь, вы поймете ее еще лучше.
Поэтому я не старался избегать настоящей математики, а объяснял ее шаг за шагом, чтобы постепенно вся математика стала для вас очевидной.
Как и многие, я когда-то думал, что математика — это запутанная наука, с которой трудно работать.
Со временем я убедился, что при правильном подходе математика почти не представляет труда.
Любая путаница в математике обычно возникает только из-за попыток слишком быстро пройти материал – тем самым пропуская важные шаги, необходимые для правильного рассуждения.
3. Зачем программисту изучать теорию вероятностей и статистику? Я искренне верю, что каждый должен в той или иной степени изучать вероятность и статистику, поскольку эти знания помогут судить о неопределенности, которая окружает нас повсюду в жизни.
Что касается программиста, то ему обязательно придется иметь дело с какими-то типовыми задачами, где полезно разбираться в статистике.
Весьма вероятно, что на каком-то этапе вашей профессиональной карьеры вам придется писать код, в котором некоторые решения принимаются на основе априорно нечетких факторов.
Возможно, это будет измерение конверсии веб-страницы, генерация какого-то случайного вознаграждения в игре, случайное распределение пользователей по группам или даже считывание информации с какого-то нечеткого датчика.
Во всех этих случаях вам очень поможет глубокое понимание теории вероятностей.
Мой собственный опыт показывает, что вероятностный подход очень полезен при отладке многих ошибок, которые трудно воспроизвести или отследить до сложной проблемы.
Если окажется, что ошибка вызвана недостатком памяти, то можете ли вы быть уверены, что ошибка будет возникать чаще, если память будет уменьшена дальше? Если сложную ошибку можно объяснить двояко, то какую возможность лучше исследовать в первую очередь? Во всех таких случаях может помочь теория вероятностей.
Конечно, развитие машинного обучения и науки о данных означает, что инженерам все чаще приходится сталкиваться с проблемами, в которых программирование предполагает непосредственную работу с вероятностями.
4. Можете ли вы кратко описать разницу между частотным и байесовским подходами к теории вероятностей? С точки зрения частоты вероятность интерпретируется как утверждение о том, как часто событие должно происходить в ходе нескольких испытаний.
Итак, если подбросить монету дважды, следует ожидать, что один раз выпадет орел, поскольку у монеты две стороны, и на одной из них изображен орел.
В байесовской интерпретации вероятность трактуется как некая характеристика нашего знания, в принципе, как продолжение логики.
Вероятность выпадения орла равна 0,5, поскольку я не вижу причин, по которым орел должен выпадать чаще, чем решка.
Итак, в случае с подбрасыванием монеты оба подхода вполне работоспособны.
Однако когда дело доходит до таких вещей, как шансы вашей любимой команды на победу в чемпионате мира, фактор уверенности становится гораздо более значимым.
Это, кстати, также означает, что байесовская статистика делает утверждения не о мире, а о нашем понимании мира.
Поскольку каждый понимает мир немного по-разному, байесовская статистика помогает нам учесть эти различия в нашем анализе.
Во многих отношениях байесовский анализ — это наука об эволюции убеждений.
5. Почему в книге основное внимание уделяется байесовскому подходу? Есть много действительно веских философских причин сосредоточиться на байесовской статистике, но меня мотивировала очень практическая причина: с байесовским подходом все имеет смысл.
Основываясь на относительно небольшом наборе интуитивных правил, вы можете разработать решение практически любой проблемы, с которой можете столкнуться.
Вот почему байесовская статистика настолько мощна и гибка и почему ее так легко изучить.
Я думаю, что байесовское рассуждение отлично подходит для программистов.
Вы не пытаетесь решить проблему с помощью импровизированных тестов, а рассуждаете о ней и постепенно приходите к действительно оправданному решению.
В принципе, байесовская статистика является рассуждением.
Вы соглашаетесь на статический анализ только в том случае, если он действительно логичен и убедителен для вас, а не потому, что ваш, казалось бы, произвольный тест дает вам какую-то столь же неподтвержденную ценность.
Кроме того, байесовская статистика позволяет усомниться в результате с качественной точки зрения.
В повседневной практике часто случается, что двум людям предъявляются одни и те же факты, но их выводы разные.
Байесовская статистика позволяет нам формально моделировать такие различия во мнениях, чтобы мы могли сами проверить, какие факты потребуются нам, чтобы изменить свое мнение.
Вам не обязательно верить результатам, записанным на бумаге, из-за какого-то значения p, вы верите им, потому что они кажутся вам действительно убедительными.
6. Как байесовская статистика связана с машинным обучением Среди сходства между машинным обучением (особенно нейронными сетями) и байесовской статистикой, о котором я подумал, заключается в том, что в обеих дисциплинах математический анализ может стать чрезвычайно сложным.
По сути, машинное обучение — это понимание и решение весьма нетривиальных производных.
Вы получаете для нее функцию и функцию потерь, затем (автоматически) вычисляете производную и пытаетесь следовать ей, пока она не приведет вас к оптимальным параметрам.
Многие ехидно отмечают, что обратное распространение ошибки — это всего лишь «цепное правило», но практически во всех сложных задачах, связанных с машинным обучением, оно используется весьма успешно.
Байесовская статистика — это еще один аспект математического анализа, связанный с решением действительно сложных интегралов.
Майкл Бетанкур, автор книги «Стэн», прекрасно отмечает, что практически весь байесовский анализ включает в себя вычисление ожиданий, то есть вычисление интегралов.
В результате байесовского анализа у вас осталось апостериорное распределение, но использовать его каким-либо образом без интегрирования и получения тем самым конкретного ответа невозможно.
К счастью, никто не делает ехидных комментариев по поводу интегралов, поскольку всем известно, что даже самый тривиальный интеграл весьма сложен.
Вот как это афористично сформулировано в одном из комиксов xkcd: 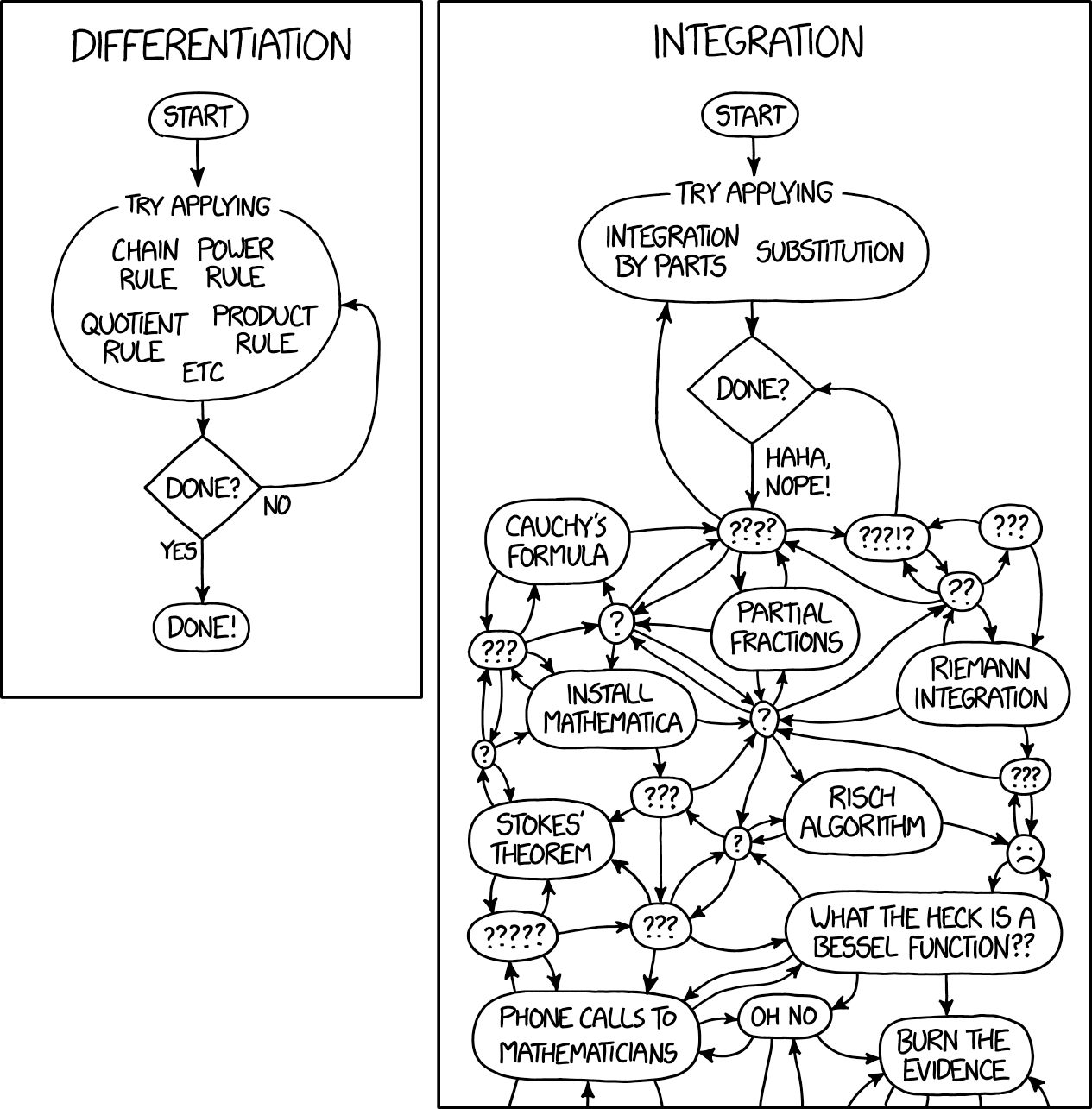
В этом странном состоянии сегодня находятся машинное обучение и байесовская статистика: мы развиваем простейшие идеи математического анализа до такой степени сложности, что их можно только вычислить.
Эти отношения также подчеркивают ключевой момент. Когда мы говорим о производных, мы ищем конкретную точку, связанную с функцией.
Итак, если вы знаете положение и время, то скорость — это производная, которая должна определять, когда вы двигались быстрее всего.
Небольшой шаг к прогрессу в ML — это когда вы рассчитали одну метрику лучше, чем кто-либо другой.
Интеграция – это суммирование всего процесса.
Опять же, если вы знаете место и время, то интеграл — это расстояние, он позволяет узнать, как далеко вы проехали.
Байесовская статистика представляет собой сумму всего, что вы знаете о проблеме, но позволяет не просто делать отдельные прогнозы, но и характеризовать степень уверенности в наших прогнозах по широкому диапазону вариантов.
Прогресс в области байесовской статистики заключается в понимании все более сложных информационных систем.
7. Если читатели захотят глубже углубиться в тему книги, какие материалы (книги, курсы, блоги) вы бы им порекомендовали? Максимальное вдохновение я черпал из книги ?.
Т.
Джейнса «Теория вероятностей: логика науки».
Я втайне надеюсь, что моя книга «Байесова статистика — это здорово» сможет стать аналогом его книги, но ориентированной на более широкий круг читателей.
Работать с книгой Джейнса — непростая задача, и она представляет собой весьма радикальную интерпретацию байесовской статистики.
Обри Клейтон оказал своим читателям большую услугу, составив цикл лекций согласно главам этой книги.
Конечно, если вам понравилась книга, вам, вероятно, понравится и мой блог.
В последнее время я там мало что пишу, так как написал книгу «Байесова статистика — это здорово», а до этого «Научимся программировать на Haskell», но сейчас голова уже разрывается от идей, и не все из них посвящены строго Байесовские темы.
Как правило, я задумываюсь над какой-то темой из области статистики/вероятности и из этой идеи аккуратно раскручиваю новую статью для блога.
8. По вашему опыту, какую концепцию вероятности/статистики особенно трудно понять? Честно говоря, самое сложное — интерпретировать вероятности.
Люди действительно потеряли веру во многих байесовских аналитиков, таких как Нейт Сильвер (и многих других), когда они предсказывали, что у Хиллари Клинтон будет 80% шанс на победу на выборах 2016 года — и она проиграла.
Люди думали, что их кто-то обманул, и все ошибались, но на самом деле вероятность в 80% — это не так уж и много.
Если врач скажет мне, что мои шансы на выживание составляют 80%, то я серьезно занервничаю.
Типичный способ решения этой проблемы — указать на вероятности как таковые и заявить, что они являются плохим выбором для выражения неопределенности.
Чтобы справиться с этим неудобством, приходится использовать коэффициенты или отношения правдоподобия или какую-то систему, подобную децибелам, например, концепцию «доказательств» Джейн.
Однако, поразмыслив довольно долго о вероятностях, я пришел к выводу, что не существует четкого способа выразить неопределенность.
Суть проблемы в том, что каждый из нас в глубине души убежден, что в мире есть определенность.
Даже у опытных специалистов по теории вероятностей есть ощущение, что, может быть, если вы проведете правильный анализ, выясните необходимые априорные данные, добавите еще один уровень в свою иерархическую модель, тогда у вас все получится, и вы избавитесь от неопределенности или хотя бы уменьшить.
Вероятность меня привлекает отчасти благодаря странному сочетанию этих двух факторов: желания разобраться в мире и осознания того, что, как бы вы ни старались, мир все равно вас чем-то удивит. 9. Что вы думаете о p-значениях как мере статистической значимости? Не могли бы вы вкратце описать, что такое p-хакинг? Что касается p-значений, часто неправильно понимаются две вещи.
Во-первых, разумный человек не стал бы пытаться отвечать на вопросы, используя значения p. Представьте, как будет выглядеть следующий разговор на работе: Менеджер: «Вы исправили эту ошибку, как было указаноЭ» Вы: «Ну, я почти уверен, что не исправил это…» Менеджер: «Если исправили, отметьте, что исправили».
Вы: «О нет, я не могу утверждать, что исправил это…» Менеджер: «Вы собираетесь поставить пометку «не буду исправлять»Э» Вы: «Нет-нет, конечно, это совсем не так».
P-значения многих сбивают с толку, поскольку они по своей сути неясны.
Байесовская статистика сообщает вам апостериорную вероятность, которая является положительным ответом на вопрос, сформулированный так, как вы хотите, чтобы на него был получен ответ. В приведенном выше диалоге байесианец говорит: «Я почти уверен, что ошибка исправлена».
Если менеджер хочет, чтобы вы ответили с большей уверенностью, тогда байесианец может собрать больше информации и сказать: «Я почти уверен, что это исправлено».
Вторая проблема — укоренившаяся привычка выбирать 0,05 как некое магическое, якобы значимое значение.
Возвращаясь к предыдущему вопросу о понимании вероятности: 5%-ная вероятность того, что событие произойдет, не означает, что это событие редкое.
У вас есть 5% шанс получить 20 очков при броске 20-гранного кубика.
Однако любой, кто играл в Dungeons and Dragons, знает, что это далеко не невозможно.
Если не считать ролевых игр, бросок кубиков — не лучший инструмент для того, чтобы отличить правду от лжи.
Вот тут-то мы и подошли к p-хакингу.
Представьте, что вы играете в «Подземелья и драконы» со своими друзьями и бросаете одновременно 20 двадцатигранных кубиков.
Затем вы указываете на единственного, у которого выпало 20 очков, и объявляете: «Я собирался бросить именно этот кубик, а все остальные были проверочными».
Формально вы действительно набрали 20 очков, но это всё равно жульничество, согласитесь.
В этом суть p-хакинга.
Вы анализируете, пока не найдете что-то «существенное», а затем утверждаете, что это то, что вы искали все время.
10. Итоговые рекомендации, какую книгу прочитать после вашей? Теперь, когда работа над книгой закончена, я могу понемногу начать наверстывать упущенное и читать те книги, которые не успел прочитать, работая самостоятельно.
Мне очень нравится «Байесовский анализ с Python» Освальдо Мартина (я знаю, что недавно он дал интервью Not Monad Tutorial).
Это отличная книга, в которой байесовский анализ рассматривается через призму PyMC3. Мир вероятностного программирования на самом деле кажется мне очень интересным, и он будет все больше становиться важной частью практической байесовской статистики.
Еще одна книга, которую я очень хочу прочитать, — «Статистическое переосмысление» Ричарда МакЭлрита.
Скоро выйдет второе издание, поэтому я немного не решаюсь покупать его прямо сейчас.
МакЭлрит предлагает самостоятельно Веб-сайт отличный выбор сопутствующих материалов.
Оба эти источника будут вам интересны после прочтения книги «Байесианская статистика – это здорово».
Наконец, я рекомендую выполнить байесовский анализ данных от Крушке.
Теги: #Машинное обучение #python #Большие данные #Статистика в ИТ #Профессиональная литература #статистика #книги #книги #Байесовский подход

-
Выбор Подходящего Ipod
19 Oct, 24 -
И Еще Раз Об Ответственности
19 Oct, 24 -
10 Карьерных Ошибок, О Которых Я Сожалею
19 Oct, 24 -
Опыт Участия В Robotchallenge 2014
19 Oct, 24 -
Первый И Двадцать Пятый
19 Oct, 24


