Мне пришла в голову немного странная мысль, что дом мог бы стать хорошей площадкой для игры в тетрис.
Недалеко от меня было всего одно подходящее для этого здание.
Результат можно увидеть на видео: Проект реализован на достаточно низком уровне, без использования какого-либо готового решения.
Источник Чаще всего сейчас используются 2 варианта реализации дополненной реальности:
- безмаркерный, т.е.
положение камеры определяется перемещением ключевых точек в ее видеопотоке;
- изображение как маркер, относительно которого находится положение камеры.
Есть еще один вариант реализации — распознавать конкретный объект и использовать его как маркер.
Это требует как минимум его наличия, но дает возможность визуально его контролировать.
Одним из методов такого распознавания является обнаружение объекта по его краям.
Имеет ограничения — объект-маркер должен иметь четко выраженные края, т.е.
объект, скорее всего, должен быть однотонным.
Или края должны быть четко определены, как, например, освещение этого здания: 
Видно, что подсветку можно легко отделить от изображения и использовать для обнаружения.
Выполнение
На Qt. Этот фреймворк позволяет работать на разных платформах и одновременно на C++.Поскольку нас волнует производительность, Pro кажется очевидным выбором.
Хоть Qt и не очень хорошо работал с Android (долгий запуск, глючная отладка), это всё компенсировалось возможностью отладки алгоритма на десктопе.
3D-графика визуализировалась с использованием необработанного OpenGL, встроенного в Qt. Работа с камерой осуществлялась средствами Qt. Для отладки записывалось видео, и было довольно удобно заменить видеопоток камеры видеопотоком из файла.
Вывод осуществлялся средствами qml. Совместная работа qml и OpenGL прошла не без проблем, но мы не будем на этом останавливаться.
Для обработки изображений включена библиотека OpenCV.
Алгоритм отслеживания
Теперь перейдем к самому интересному — алгоритму слежения за объектом по его краям.И давайте начнем с выделения краев на изображении.
Все ребра в нашем случае выглядят как прямые линии, поэтому первая мысль, которая приходит в голову — использовать детектор линий.
Его можно использовать в качестве детектора линии.
Однако этот путь мне кажется не очень правильным, так как преобразование Хафа довольно дорогое, к тому же этот детектор не очень надежный (это субъективно, возможно, все зависит от задачи).
Вместо этого давайте пойдем другим, более общим путем.
Мы не будем учитывать, что наши линии прямые, а просто будем работать на бинарном изображении.
Наличие краев будет закодировано в двоичное изображение.
Те.
пиксель со значением, равным нулю, означает, что в этом месте есть край, значение пикселя больше нуля означает, что края нет. Это изображение можно получить с помощью Детектор границ Канни или с простым пороговое преобразование .
Эти алгоритмы можно найти в OpenCV. У OpenCV теперь есть еще одна полезная для нас функция — расстояниеПреобразование , который принимает на вход двоичное изображение и выводит изображение, пиксели которого кодируют расстояние до ближайшего нулевого пикселя.
Теперь давайте предположим, что у нас уже есть первое хорошее приближение того, где должна располагаться наша модель.
Далее опишем функцию ошибок, которая описывает, насколько края нашей аппроксимации не совпадают с краями полученного изображения.
С помощью изображения от distanceTransform мы уже можем это сделать.
А затем запускаем алгоритм оптимизации функции, меняя лишь нашу аппроксимацию положения объекта в пространстве.
В результате наше приближение должно достаточно точно описывать фактическое положение объекта.
В результате алгоритм можно разделить на два этапа:
- Предварительная обработка изображения — бинаризация, фильтрация и применение функции distanceTransfrom.
- Отслеживание — оптимизация функции ошибок.
Предварительная обработка изображений
На этом этапе необходимо выделить края на изображении.Можно использовать детектор границ Канни, но в нашем случае лучше работает обычное пороговое преобразование или его адаптивная версия (в OpenCV это функции Threshold или AdaptiveThreshold).
Понятно, что такое изображение будет иметь шум, поэтому необходима фильтрация.
Сделаем это следующим образом — выделим контуры с помощью функции OpenCV. найтиКонтуры и удалите сегменты, которые слишком малы или недостаточно похожи на линии.
Результат обработки можно увидеть на изображении: 
Последовательно: исходное изображение -> после порогового преобразования -> после фильтрации.
Это изображение уже достаточно четко говорит нам, где нужное ребро, а где его нет. После этого мы используем функцию distanceTransform, и в результате у нас будет информация о том, насколько далеко каждая точка находится от края.
Обозначим полученное изображение как 
.
Вот как это выглядит в нормализованном и визуализированном виде: 
Далее нам понадобятся некоторые математические инструменты.
Алгоритм оптимизации функции
Оптимизация функции — это задача поиска минимума функции.Если мы имеем дело с линейной системой уравнений, то найти минимум достаточно просто.
Представим систему уравнений в матричной форме: 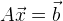
, то наше решение: 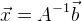
.
Если у нас есть переопределенная система уравнений, то мы можем использовать метод наименьших квадратов : 
.
Если наша функция нелинейная, то задача усложняется.
Чтобы найти минимум, вы можете использовать Алгоритм Гаусса-Ньютона .
Алгоритм работает следующим образом:
- Предполагается, что у нас уже есть некоторое начальное приближение решения
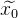
, который мы будем уточнять итеративно. - Используя расширение Тейлора, мы можем приблизить нашу нелинейную функцию к линейной в точке текущего приближения.
Решаем полученную линейную систему уравнений методом наименьших квадратов, получая

.Полученное решение не будет решением, но оно будет ближе, чем текущие приближения.
- Заменить текущее приближение
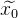
полученное решение
и переходим к шагу 2. Повторяем это до тех пор, пока разница между
И
не упадет ниже определенного значения.
Позволять 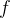
- рабочая функция, 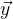
— вектор заранее известных значений функции.
Учитывая идеальное решение уравнения 
следующее утверждение верно 
.
Но у нас есть только приблизительное представление о нем.
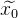
.
Тогда мы обозначим вектор ошибки из этого приближения как: 
.
И общая ошибка функции будет: 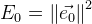
.
Теперь найдя такой 
, при котором 
достигнет минимума, мы получим лучшее приближение решения 
.
Начиная с подхода 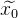
будем итеративно аппроксимировать его, получая на каждой итерации 
.
Для этого нам нужно просчитать каждую итерацию Матрица Якоби для функции 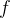
для текущего приближения, состоящего из производных нашей функции: 
И следующее приближение задается как: 
.
Часто задачи структурированы таким образом, что мы имеем большой объем данных, независимых друг от друга (только по значениям 
).
В результате общая матрица Якобиана оказывается очень разреженной.
Есть способ оптимизировать расчеты.
Предположим, у нас есть общая функция, рассчитанная по набору точек.
От дж -й балл, который мы получаем 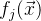
.
Вместо вычисления матрицы Якобиана 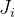
для всей функции мы вычисляем матрицу Якобиана специально для 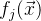
и обозначим это как: 
.
Тогда следующее приближение будет иметь вид: 
.
Кроме того, это изменение позволяет распараллеливать вычисления.
Может случиться так, что следующее значение
даст большую ошибку, чем 
.
Для решения этой проблемы можно использовать модификацию алгоритма — Алгоритм Левенберга-Марквардта .
Добавить значение 
в нашу формулу: 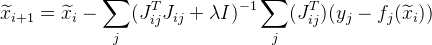
, Где 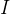
является единичной матрицей.
Значение 
выбирается следующим образом:
- сначала оно имеет некоторое достаточно малое значение (такое, что алгоритм сходится);
- тогда, если ошибка связана с
больше, чем
, затем увеличьте значение
и попытайтесь вычислить ошибку для
снова.
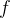
, тем больше должно быть значение

.
Однако чем выше значение 
, тем медленнее сходится алгоритм.
Завершим алгоритм, когда
отличается от 
до достаточно малого значения и принять
как решение.
Алгоритм достаточно универсален и может использоваться для самых разных задач.
Математическая модель отслеживания
Поскольку мы имеем дело с координатами в пространстве, то понятно, что нужно уметь манипулировать этими координатами.
Предположим, у нас есть некоторый набор точек 
.
И нам нужно повернуть их вокруг точки с нулевыми координатами.
Вероятно, проще всего использовать матрицу вращения.
р , описывающая требуемый поворот: 
.
Если нам нужно сместить точки, то просто добавляем нужный вектор т : 
.
Таким образом, вы можете менять положение объекта в пространстве по своему усмотрению.
Оказывается, координаты объекта задаются трёхмерной матрицей р и трехмерный вектор т , т.е.
12 параметров.
Более того, эти параметры не являются независимыми друг от друга; компоненты матрицы вращения связаны между собой определенными условиями.
Поэтому с точки зрения использования этих параметров при оптимизации функции эти параметры не являются лучшим решением.
Параметров больше, чем степеней свободы; между ними существует зависимость.
Есть еще одна форма ротации – Формула вращения Родрига .
Это вращение задается тремя параметрами, образующими трехмерный вектор.
Нормализованный вектор — это ось вращения, а длина этого вектора — это угол вращения вокруг этой оси.
Зададим функцию вращения вектора в : 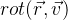
использование параметров р Формулы Родригеса.
Отсюда мы получаем следующую формулу: 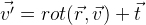
.
И в результате мы можем указать координаты положения объекта 6-мерным вектором: 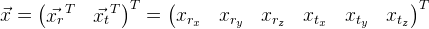
Получаем следующую формулу: 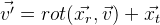
.
Модель камеры-обскуры
Теперь опишем простую математическую модель камеры, используемой в проекте:Где
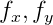
— фокусное расстояние в пикселях;
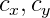
— оптический центр также в пикселях.
Это индивидуальные параметры камеры, которые называются внутренними параметрами камеры.
Обычно эти параметры известны заранее.
В данном проекте эти параметры подбирались на глаз.
Данная модель не учитывает искажения объектива камеры ( искажение ).
Предположим, их не существует. С помощью этой модели мы получаем центральную проекцию, все точки которой стремятся к оптическому центру, чем дальше они расположены, тем дальше от камеры.
Таким образом мы получаем эффект сужающейся железной дороги: 
В пространстве камера совмещена с осью я , плоскость изображения параллельна плоскости ху .
Дополним нашу модель возможностью перемещения в пространстве:
Таким образом, мы получили модель, с помощью которой можно алгебраически моделировать проекцию точек внешнего мира на изображение камеры (от мировых координат до экранных координат).
В этой модели нам остаются неизвестными параметры взаимного положения камеры в пространстве.
.
Эти параметры называются внешними характеристиками камеры (внешние параметры камеры).
Отслеживание
Реализовано без инструментов OpenCV. Во-первых, нам нужно получить функцию ошибок для нашего приближенного решения, которое было описано выше.И опишем его расчет пошагово:
- Выбираем такие края модели слежения, которые видны, исходя из параметров текущей аппроксимации.
- Превращаем выбранный набор ребер в фиксированный набор точек для упрощения вычислений.
Можно, например, взять с каждого края n-ное количество точек или (более правильный вариант) выбрать такое количество, чтобы между точками было фиксированное расстояние в пикселях.
Назовем их контрольными точками (в проекте: controlPoint — контрольные точки и controlPixelDistance — то самое фиксированное расстояние в пикселях).
- Проецируем контрольные точки на изображение.
Благодаря расстояниеИзображение мы можем получить расстояние проекции контрольной точки до края изображения.
В идеале все контрольные точки должны лежать строго по краям изображения, т.е.
расстояние до края должно быть равно нулю.
На основании этого получаем ошибку для конкретной контрольной точки:

. - Мы получаем следующую функцию ошибки:
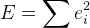
Для этого воспользуемся описанным выше алгоритмом Левенберга-Марквардта.
Как мы уже знаем, алгоритм требует вычисления матрицы Якобиана, т.е.
производных функций.
Можно использовать численное определение производных.
Вы также можете использовать некоторые готовые решения этого алгоритма.
Однако в этом проекте все было написано вручную, поэтому я опишу полный вывод всего решения.
Для каждой контрольной точки получаем уравнение, независимое от других точек.
Выше уже было описано, что в этом случае можно рассматривать эти уравнения независимо друг от друга, вычисляя матрицу Якобиана конкретно для каждого.
Давайте рассмотрим это по порядку, используя правила дифференцирования сложной функции: 
Обозначим 
, Затем 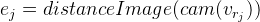

Отсюда: 
Далее мы обозначим 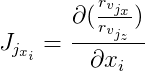
И 
, Затем: 
Производные изображения расстояниеИзображение находятся численно.
И для расчета векторов 
И 
вам нужно будет найти производные, используя формулу вращения Родрига.
Я нашел якобиан, используя эту формулу в публикации «Компактная формула для производной трехмерного вращения в
экспоненциальные координаты» Гильермо Гальего, Энтони Йецци : 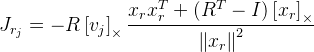
,
Где р — матрица вращения, полученная по формуле Родригеса из вектора вращения 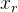
;
— точка, которую мы вращаем; я - единичная матрица; 
.
Как мы видим здесь, у нас происходит деление на длину вектора вращения, и если вектор равен нулю, то формула уже не работает. Вероятно, это связано с тем, что при нулевом векторе не определена ось вращения.
Если вектор вращения очень близок к нулю, то используем такую формулу: 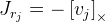
.
Осталось только покрасить 
И 
(здесь индекс дж опущено): 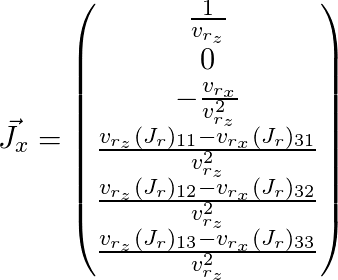

Таким образом, мы получили матрицу Якобиана для нужной нам точки и можем использовать ее для описанного выше алгоритма оптимизации.
У этого алгоритма есть несколько проблем.
Во-первых - точность.
В результате глобальное положение камеры незначительно меняется от кадра к кадру.
Мы можем это немного исправить.
У нас есть априорная информация, что положение камеры не может резко меняться от кадра к кадру.
И мы можем уменьшить этот джиттер, добавив в функцию дополнительные уравнения.
Следует помнить, что векторное смещение т в нашем случае это не координата глобального положения камеры.
Глобальная позиция — это локальная точка с нулевыми координатами, поэтому ее можно определить следующим образом: 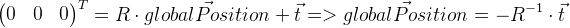
Мы запоминаем положение предыдущего кадра в предыдущаяGlobalPosition .
Теперь предыдущая позиция должна быть близка к нулю, т.е.
длина вектора 
должно быть достаточно маленьким.
Те.
Необходимо минимизировать, помимо других значений невязки, вектор д .
Для определения степени влияния данной модификации введем значение 
и умножить перед добавлением вектора д на 
: 
Теги: #Android #Разработка Android #математика #Алгоритмы #AR и VR #дополненная реальность #AR #tetris #дополненная реальность #Qt #отслеживание на основе моделей

-
Пробелы — Главный Враг Linux
19 Oct, 24 -
Два В Одном
19 Oct, 24 -
Еще Один Луч Ненависти
19 Oct, 24 -
Радио-Т №72
19 Oct, 24 -
Hp Storageworks P2000: Новое Лицо Msa
19 Oct, 24


