Геометрическое Представление Кривизны Пространства В Метрике Шварцшильда

Об этом говорит вся история физики – любая эмпирически полученная формула со временем получает теоретическое обоснование, объясняющее смысл всех содержащихся в ней математических форм.

Обычно в представлении этой метрики часть, связанная с физическими константами и массой тела, создающего поле, выражается через радиус Шварцшильда:



поскольку в этой точке метрика имеет особенность.

Здесь время буквально останавливается.

В данном случае вот как выглядит вся метрика:



Но в продолжение рассуждений о физической сущности явлений вот эти два:



тоже надо понять.

Итак, давайте представим это так:



Это всего лишь половина гравитационного радиуса



, и его размеры одинаковы.

Мы получаем:



Возникает вопрос:







Уже неплохо.

Давайте нарисуем это.

Давайте представим



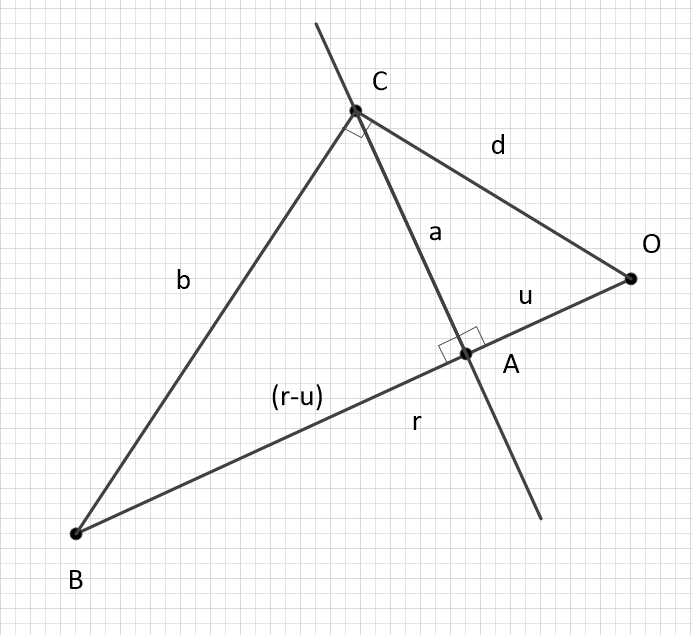
последний сегмент



- его часть, как показано на рисунке ниже.

Это очевидно, что



.

Интересно, кстати, что из



следует, что точка



находится за (ниже) горизонта событий энергетического объекта



.

Его так легко найти, но мы не можем.

Теперь мы покажем, что отношение вида



будет осуществляться для всех точек, имеющих геометрическое расположение перпендикулярно



в точку



:







для любого



И



.

Проще говоря, разность квадратов



эквивалентна разности любых величин, проекции которых на



являются



И



соответственно, при условии, что точка



у них есть общее.

Предположим далее, что



И



, наоборот, прогнозы



по некоторым осям, то есть пифагорова сумма двух величин, в исходном виде перпендикулярных друг другу.

Преобразуя это в требование, рассмотрим случай



, для которого верно следующее:







Давайте завершим это



аналогично начальной итерации:







Это четвертая степень.

Формула объема трехмерного шара:



Я имею в виду, что если вы умножаете и делите



на



:



тогда множитель в метрике Шварцшильда превращается в разность объемов двух 3-сфер, построенных вокруг двух радиальных проекций точки относительно центра поля, отнесенную к объему 3-сферы, образованной суммарным расстоянием между точка и центр поля.

С учетом того, что полный радиус задается проекциями, вся эта структура очень лаконично определяется двумя параметрами, один из которых связан с энергией, а второй — нет. Имеются ровно две координаты.

За его пределами можно спрятать что-то тяготящее, но невидимое.

2. Наличие второй скрытой координаты устраняет парадокс нулевого времени.

3. Поскольку кривизну пространства вокруг массивного тела всегда можно разложить на две составляющие, одна из которых связана с энергией тела, а вторая исключительно с пространством, то следующим шагом является решение уравнений общей теории относительности для вакуумного случая пятимерного пространства-времени.

Подробнее об этом в следующей статье.

Давайте выразим величины



И



через угол



:



.

Давай позвоним ему угол кривизны траектории.

Тогда множитель можно выразить очень по-разному:







Мне особенно нравится вариант с касательными.

Подставим в исходный интервал:



Все, как и должно, превращается в плоскую метрику Минковского при



.

Здесь обязательно должен быть пятый.