Геодезические купола, пожалуй, сложно назвать чем-то необычным или новым.
В этой заметке я расскажу вам немного об этих конструкциях в целом, об их устройстве, а также покажу на примере, как я что-то задумал на эту тему.
Код тоже будет. 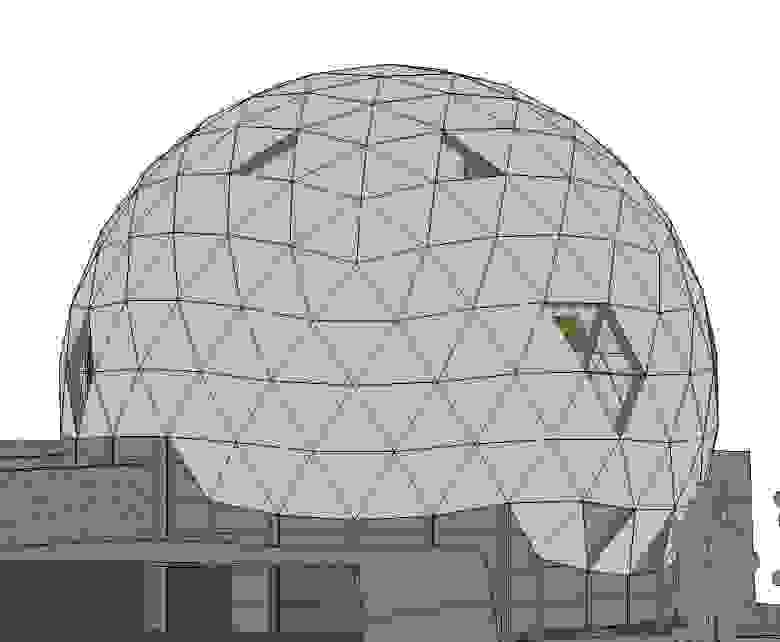
Я не буду цитировать Википедию.
Почему я выбрал купол своим домом?
- При равном объёме площадь поверхности сферы будет меньше, чем у любой другой формы.
Это положительно влияет как на расход материала, так и на энергопотребление в процессе эксплуатации.
- Мне нравится, как выглядит сфера.
- Это интересный инженерный проект, в каком-то смысле даже вызов.
Это сложно, сложно и поэтому весело!
Попробуем разобраться в этом посте.
Основой таких структур является икосаэдр или октаэдр.
В целом это правильный многогранник.
В моем случае это был икосаэдр и он используется чаще.
Далее берем одну грань и заменяем ее несколькими треугольниками, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра.
Звучит не слишком сложно.
Давай возьмем перерыв.
Есть замечательный калькулятор www.acidome.ru что позволяет вращать геодезиста в реальном времени.
За основу берем икосаэдр, устанавливаем частоту 1, а часть сферы 1/1. 
Это наш основной икосаэдр.
Частота — это то, на сколько частей мы разбиваем каждое ребро икосаэдра.
Ставим 3,4,5 и ничего не становится понятно.
Переключитесь в режим крыши и ищите пятиугольники.
В тех местах, где у нас находится вершина икосаэдра, будет пятиугольник.
Между тремя пятиугольниками находится грань икосаэдра.

Если внимательно посмотреть на геодезическую и знать, что искать (обычно пятиугольник), то станет видна правильность структуры.
В «Биосфере» в Монреале при должном старании можно найти пятиугольники и посчитать их частоту.
Наша частота равна количеству рёбер между двумя пятиугольниками.
Сами «большие» треугольники, с вершинами в вершинах икосаэдра, также имеют структуру.
На ацидоме в режиме руля это видно по цвету.
Треугольники расположены симметрично относительно центра «большого» треугольника.
Число их типов меньше общего числа треугольников.
В случае частоты 5 уникальных треугольников 9. 
Проектируя дом, передо мной стояла задача построить в Динамо сферу.
Это инструмент, позволяющий научить Autodesk Revit работать со сложными формами.
Это среда визуального программирования.
Погуглив, я даже нашел эскиз построения геодезической сферы в «Динамо».
Он построил сферу, но не ту.
Вот в чем дело.
Когда мы берем одно ребро икосаэдра и делим его на маленькие треугольники, то есть несколько способов сделать это.
В ацидоме за это отвечает переключатель «метод расщепления».
На найденном мной эскизе сфера построена методом равных хорд. Что это значит? Берем большой треугольник икосаэдра, делим каждое его ребро на нужное нам количество частей, соединяем точки на ребрах друг с другом и получаем плоскую сетку из треугольников.
Затем мы проецируем эту сетку на сферу.
Все бы ничего, но сами эти треугольники совсем разные по размеру.
Центральный – самый большой.
Это понятно; центр «большого» треугольника находится на максимальном расстоянии от сферы.
Это плохо, поскольку в этом случае сложнее оптимизировать расход материалов.
Будет больше мусора.
Другой способ разбиения (с равными дугами) предполагает, что мы строим дуги поверх «большого» треугольника и делим их на равные части.
Подход другой; простой проекции недостаточно.
Эскиз не подошёл.
Я пытался это исправить и в итоге мне пришлось погрузиться с головой в это дело.
Как оказалось, помимо визуальной среды, в Dynamo есть встроенный Python. Я с этим языком раньше не сталкивался, но куда же не исчез наш? В конце концов, это всего лишь инструмент. Дальше будут куски кода, обратите внимание, что это мой hello world на питоне, и целью было не построить максимально эффективное и продуктивное решение, а построить нужную сферу.
Метод равной дуги.
Берем одну из граней икосаэдра и строим дуги из углов этого треугольника.
Теги: #Научно-популярная #Будущее уже здесь #геодезический куполfor k, edge in enumerate(curves):

-
Футболки С Видеоиграми
19 Oct, 24 -
Абд Открывает Fit Academy Russia
19 Oct, 24 -
Интеграция Проекта Vuejs+Ts С Sonarqube
19 Oct, 24 -
Казалось Бы, Простой Вопрос О Javascript
19 Oct, 24 -
Список Запатентованных Жестов
19 Oct, 24 -
Умные Замки
19 Oct, 24


