Сущность генетических алгоритмов Данная тема посвящена решению задач оптимизации с использованием генетических алгоритмов в среде.
МАТЛАБ .
Заранее извиняюсь за большой объем данных: это связано с тем, что при написании темы основной задачей было подробно раскрыть каждый из параметров генетических алгоритмов, которые можно настроить в MATLAB. Генетические алгоритмы это метод решения проблемы оптимизации , основанный на биологических принципах естественного отбора и эволюции.
Генетический алгоритм повторяет процедуру модификации популяции (набора индивидуальных решений) определенное количество раз, тем самым достигая новых наборов решений (новых популяций).
При этом на каждом этапе из популяции выбираются «родительские особи», то есть решения, совместная модификация (скрещивание) которых приводит к образованию новой особи в следующем поколении.
Генетический алгоритм использует три типа правил, на основе которых формируется новое поколение: правила отбора, скрещивания и мутации.
Мутация позволяет, внося изменения в новое поколение, избежать попадания в локальные минимумы оптимизируемой функции.
(Под катом основная часть + несколько скриншотов).
Механизм работы с генетическими алгоритмами в среде MATLAB реализован двумя способами: 1. Вызов функции генетических алгоритмов 2. Использование инструмента генетического алгоритма Оба метода предоставляются как часть стандартного набора функций и модулей MATLAB. На мой взгляд, второй способ работы с генетическими алгоритмами в MATLAB, связанный с использованием модуля Genetic Algorithm Tool, гораздо удобнее и нагляднее.
Давайте посмотрим на это более подробно.
Работа с ИНСТРУМЕНТОМ ГЕНЕТИЧЕСКОГО АЛГОРИТМА
Чтобы запустить Инструмент генетического алгоритма, запустите команду gatool в командной строке MATLAB. После этого запустится пакет генетических алгоритмов и на экране появится главное окно утилиты.
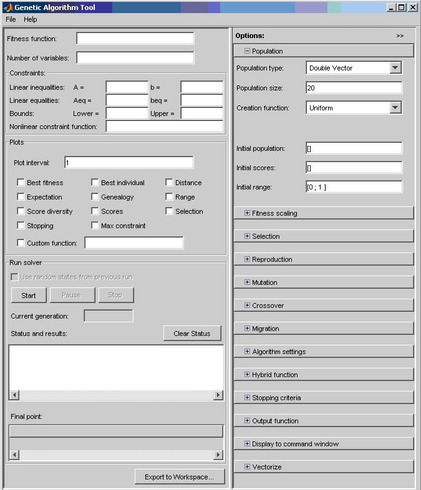
В поле Фитнес-функция оптимизируемая функция указывается в виде @fitnessfun, где Fitnessfun.m — имя М-файла, в котором предварительно должна быть описана оптимизируемая функция.
На всякий случай отмечу, что М-файл создается в среде MATLAB через меню Файл-> Новый-> М-Файл.
Пример описания некоторой функции my_fun в М-файле: функция z = my_fun(x) z = x(1)^2 – 2*x(1)*x(2) + 6*x(1) + x(2)^2 – 6*x(2); Вернёмся в главное окно утилиты GATool. Поле Число переменных указывает длину входного вектора оптимизируемой функции.
В приведенном выше примере функция my_fun имеет входной вектор длиной 2. На панели «Ограничения» вы можете установить ограничения или функцию нелинейного ограничения.
В поле Линейные неравенства задается ограничение линейного неравенства вида: А*х ≤ б.
В поле Линейные равенства этой панели задаются ограничения линейного равенства: А*х = б.
В обоих случаях A — некоторая матрица, b — вектор.
В поле Границы нижние и верхние ограничения переменных задаются в векторной форме, а в поле Функция нелинейного ограничения можно указать произвольную функцию нелинейного ограничения.
Если конкретная задача не требует установки ограничений, все поля на панели «Ограничения» следует оставить пустыми.
Ниже находится панель настроек графика.
Он позволяет отображать различные графики, отображающие информацию о работе генетического алгоритма.
На основании этой информации вы можете изменить настройки алгоритма, чтобы повысить его эффективность.
Например, выбор опции Best Fitness на этой панели позволяет отобразить на одном графике лучшее и среднее значение оптимизируемой функции для каждого поколения алгоритма.
Подробнее эта панель будет описана ниже вместе с другими панелями вкладки «Параметры» утилиты GATool. Панель «Запустить решатель» содержит элементы управления (кнопки «Старт», «Пауза» и «Стоп» для запуска, временной и полной остановки работы генетического алгоритма).
Также он содержит поля Статус и результаты, в которых отображаются текущие результаты работы генетического алгоритма, и Конечная точка, в котором отображается значение конечной точки алгоритма — лучшее значение оптимизируемой функции (то есть искомое значение ).
В правой части главного окна утилиты GATool находится панель «Параметры».
Он позволяет задавать различные настройки работы генетических алгоритмов.
При нажатии на кнопки [+], которые расположены напротив названия каждого из настраиваемых параметров на панели «Параметры», появляются раскрывающиеся списки (вкладки), содержащие поля для ввода и изменения соответствующих параметров генетического алгоритма.
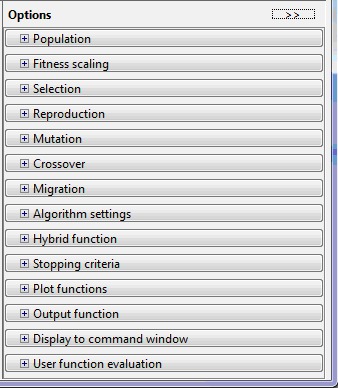
Основными настраиваемыми параметрами в GATool являются:
— население (вкладка «Население»);
— масштабирование (вкладка Fitness Scaling);
— оператор выбора (вкладка «Выбор»);
— оператор воспроизведения (вкладка «Воспроизведение»);
— оператор мутации (вкладка «Мутация»);
— оператор пересечения (вкладка Crossover);
— перемещение особей между популяциями (вкладка «Миграция»);
— специальные параметры алгоритма (вкладка «Настройки алгоритма»);
— настройка гибридной функции (вкладка «Гибридная функция»);
— установка критерия остановки алгоритма (вкладка «Критерии остановки»);
— отображение различной дополнительной информации в процессе работы генетического алгоритма (вкладка «Функции построения графика»);
— вывод результатов работы алгоритма в виде новой функции (вкладка «Выходная функция»);
— задание набора информации, выводимой в командное окно (вкладка «Отображать в командном окне»);
— метод расчета значений оптимизируемых и предельных функций (вкладка «Оценка пользовательских функций»).
Давайте подробнее рассмотрим все вышеперечисленные вкладки панели «Параметры» и содержащиеся в них элементы.
Во вкладке настроек популяции пользователь имеет возможность выбрать тип математических объектов, к которым будут принадлежать особи всех популяций (двойной вектор, битовая строка или пользовательский тип).
Следует учитывать, что использование битовой строки и пользовательских типов накладывает ограничения на список допустимых операторов создания, мутации и скрещивания особей.
Например, при выборе битовой строки в качестве формы представления особей для оператора пересечения нельзя использовать гибридную функцию или нелинейную ограничивающую функцию.
Также вкладка «Популяция» позволяет настроить размер популяции (из скольких особей будет состоять каждое поколение) и способ создания начального поколения (Равномерное — если не наложено ограничений, в противном случае — Реализуемая популяция).
Кроме того, в этой вкладке можно вручную задать начальное поколение (с помощью пункта «Начальная популяция») или его часть, начальный рейтинг особей (пункт «Начальные баллы»), а также ввести ограничительный числовой диапазон, в котором находятся особи должна принадлежать начальная популяция (Начальный диапазон).
Во вкладке Fitness Scaling пользователь имеет возможность указать функцию масштабирования, преобразующую значения, достигаемые оптимизируемой функцией, в значения, находящиеся в пределах, допустимых для оператора выбора.
При выборе параметра Rank в качестве функции масштабирования масштабирование будет сведено к рейтингу, то есть индивидам присваивается рейтинговый номер (лучшему индивидууму - один, следующему - два и так далее).
Пропорциональное масштабирование устанавливает вероятности, пропорциональные данному числовому ряду для отдельных лиц.
При выборе варианта «Топ» наибольшее значение рейтинга присваивается сразу нескольким наиболее выдающимся личностям (их количество указывается в качестве параметра).
Наконец, при выборе типа линейного масштабирования Shift можно указать максимальную вероятность лучшей особи.
Вкладка «Выбор» позволяет выбрать родительский оператор выбора на основе данных функции масштабирования.
Для выбора доступны следующие параметры оператора выбора: — Турнир – случайным образом выбирается определенное количество лиц, среди них на конкурсной основе выбираются лучшие; — Рулетка – имитирует рулетку, в которой размер каждого сегмента задается в соответствии с его вероятностью; — Равномерное — родители выбираются случайным образом по заданному распределению и с учетом количества родительских особей и их вероятностей; - Стохастическая равномерная - строится линия, в которой каждому родителю присваивается часть определенного размера (в зависимости от вероятности родителя), затем алгоритм пробегает линию шагами одинаковой длины и выбирает родителей в зависимости от того, какая часть линии, на которую приходится шаг.
На вкладке «Воспроизведение» указывается, как создаются новые особи.
Пункт «Количество элит» позволяет указать количество особей, которые гарантированно перейдут в следующее поколение.
Пункт «Доля скрещивания» указывает долю особей, созданных в результате скрещивания.
Оставшаяся часть создается мутацией.
На вкладке «Оператор мутации» выберите тип оператора мутации.
Доступны следующие варианты: — Гауссово — добавляет небольшое случайное число (согласно распределению Гаусса) ко всем компонентам каждого отдельного вектора; — Равномерный — компоненты вектора выбираются случайным образом и вместо них записываются случайные числа из допустимого диапазона; — Адаптивная осуществимая — генерирует набор направлений в зависимости от последних наиболее удачных и неудачных поколений и с учетом наложенных ограничений перемещается по всем направлениям на разную длину; — Пользовательский — позволяет установить собственную функцию.
Вкладка «Кроссовер» позволяет выбрать тип оператора кроссовера (одноточечный, двухточечный, эвристический, арифметический или рассеянный, который генерирует случайный двоичный родительский вектор соответствия).
Также можно указать собственную функцию пересечения.
На вкладке Миграция можно настроить правила, по которым особи будут перемещаться между субпопуляциями внутри одной популяции.
Субпопуляции создаются, когда размер популяции указывается как вектор, а не как натуральное значение.
В этой вкладке можно указать направление миграции (вперед – к следующей субпопуляции, обе – к предыдущей и следующей), долю мигрирующих особей и частоту миграции (сколько поколений проходит между миграциями).
Если создание подгрупп не требуется, эту вкладку всегда следует оставлять без изменений.
Вкладка специальных параметров алгоритма позволяет настроить параметры решения системы нелинейных ограничений, налагаемых на алгоритм.
Значение параметра Начальный штраф определяет начальное числовое значение критики алгоритма; Штрафной коэффициент используется как множитель этого значения в тех случаях, когда разработчика не устраивает точность оптимизации или при превышении границ, определенных на вкладке ограничений.
Как правило, эти опции детально настраиваются для решения задач высокой сложности.
Вкладка «Гибридная функция» позволяет указать другую функцию минимизации, которая будет использоваться после завершения работы алгоритма.
Следующие функции, встроенные в среду MATLAB, доступны как возможные гибридные функции: − нет (не используйте гибридную функцию); − fminsearch (поиск минимального значения); − Patternsearch (поиск по шаблону); − fminunc (для неограниченного алгоритма); − fmincon (для алгоритма с заданными ограничениями).
На вкладке Критерии остановки указаны ситуации, в которых алгоритм останавливается.
В этом случае можно настроить следующие параметры: — Generations — максимальное количество поколений, при превышении которого произойдет остановка; — Time limit – ограничение времени работы алгоритма; — Предел пригодности – если оптимизируемое значение меньше или равно этому пределу, алгоритм остановится; — Stall Generations — количество несколько отличающихся поколений, после которых алгоритм остановится; — Ограничение времени простоя – то же, что и предыдущий параметр, но применимо ко времени работы алгоритма; — Допуск функции и Допуск нелинейного ограничения — минимальные значения изменения оптимизируемой и ограничительной функций соответственно, при которых алгоритм продолжит работать.
Особый интерес представляет вкладка «Функции графика», которая позволяет выбирать различную информацию, которая отображается в процессе работы алгоритма и показывает как корректность его работы, так и конкретные результаты, достигнутые алгоритмом.
Наиболее важными параметрами, используемыми для отображения, являются: — Интервал графика — количество поколений, после которого происходит следующее обновление графиков; — Лучшая пригодность — вывод лучшего значения оптимизируемой функции для каждого поколения; — Лучшая особь — выход лучшего представителя поколения с лучшим результатом оптимизации в каждом поколении; — Distance — вывод интервала между значениями особей в поколении; — Ожидание — отображает количество вероятностей и соответствующих им особей поколений; — Генеалогия – вывод генеалогического древа физических лиц; — Диапазон — вывод наименьшего, наибольшего и среднего значений оптимизируемой функции для каждого поколения; — Разнообразие оценок — отображение гистограммы рейтинга в каждом поколении; — Очки — отображает рейтинг каждой особи в поколении; — Отбор – вывод гистограммы родителей; — Остановка – отображает информацию о состоянии всех параметров, влияющих на критерии остановки; — Пользовательский — отображает на графике определенную пользователем функцию.
Вкладка вывода результатов в виде новой функции (Вывод функции) позволяет включить вывод истории алгоритма в отдельное окно с заданным интервалом генерации (флаг История в новое окно и поле Интервал соответственно) , а также позволяет установить и отобразить произвольную функцию вывода, указанную в функции «Пользовательское поле».
На вкладке Оценка пользовательских функций описан порядок расчета значений оптимизируемых и ограничивающих функций (отдельно, параллельно в одном вызове или одновременно).
Наконец, вкладка Display to Command Window позволяет вам настроить информацию, которая отображается в главном командном окне MATLAB во время работы алгоритма.
Возможны следующие значения: Off – нет вывода в командное окно, Iterative – выводить информацию о каждой итерации работающего алгоритма, Diagnose – выводить информацию о каждой итерации и дополнительную информацию о возможных ошибках и измененных ключевых параметрах алгоритма, Final – отображается только причина остановки и конечное значение.
P.S. При написании этой темы автор использовал личный опыт и помощь среды MATLAB. В будущих статьях я постараюсь раскрыть описанный выше механизм gatool на конкретных примерах, как классических (оптимизация линейной функции, задача о стрельбе и коммивояжер), так и некоторых конкретных.
П.
П.
С.
Спасибо за внимание тем, кто дочитал до конца.
Теги: #генетические алгоритмы #matlab #gatool #задача оптимизации #Алгоритмы #matlab

-
Джевонс, Уильям Стэнли
19 Oct, 24 -
Кривая Helvetica В Opera Под Ubuntu
19 Oct, 24 -
Ссылки: Отладка Js В Браузерах
19 Oct, 24 -
Skype В России: Расставляем Все Точки Над I
19 Oct, 24 -
Об Автономном Тв-Тюнере
19 Oct, 24


