Эта статья является продолжением поста Генераторы непрерывно распределенных случайных величин .
В этой главе учтено, что все теоремы из предыдущей статьи уже доказаны и указанные в ней генераторы уже реализованы.
Как и раньше, у нас есть базовый генератор натуральных чисел от 0 до RAND_MAX:
С дискретными величинами все более интуитивно понятно.unsigned long long BasicRandGenerator() { unsigned long long randomVariable; // some magic here .return randomVariable; }
Функция распределения дискретной случайной величины: 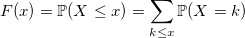
Несмотря на простоту распределений дискретных случайных величин, генерировать их иногда сложнее, чем непрерывные.
Начнем, как и в прошлый раз, с тривиального примера.
Распределение Бернулли


Возможно, самый быстрый и очевидный способ сгенерировать случайную величину с распределением Бернулли — сделать это следующим образом (все генераторы возвращают двойное значение только для согласованности интерфейса):
void setup(double p) {
unsigned long long boundary = (1 - p) * RAND_MAX; // we storage this value for large sampling
}
double Bernoulli(double) {
return BasicRandGenerator() > boundary;
}
Иногда можно сделать это быстрее.
«Иногда» означает «в случае, когда p представляет собой степень 1/2».
Дело в том, что если целое число, возвращаемое функцией BasicRandGenerator(), является равномерно распределенной случайной величиной, то каждый ее бит распределен равномерно.
Это означает, что в двоичном представлении число состоит из битов, распределенных по Бернулли.
Поскольку в этих статьях функция базового генератора возвращает unsigned long long, у нас есть 64 бита.
Вот трюк, который можно проделать для p = 1/2: double Bernoulli(double) {
static const char maxDecimals = 64;
static char decimals = 1;
static unsigned long long X = 0;
if (decimals == 1)
{
/// refresh
decimals = maxDecimals;
X = BasicRandGenerator();
}
else
{
--decimals;
X >>= 1;
}
return X & 1;
}
Если время работы функции BasicRandGenerator() недостаточно короткое, а криптоустойчивостью и размером периода генератора можно пренебречь, то для таких случаев существует алгоритм, использующий только одну равномерно распределенную случайную величину для любого объема выборки из распределения Бернулли: void setup(double p) {
q = 1.0 - p;
U = Uniform(0, 1);
}
double Bernoulli(double p) {
if (U > q)
{
U -= q;
U /= p;
return 1.0;
}
U /= q;
return 0.0;
}
Почему этот алгоритм работает? 

Равномерное распределение


Я уверен, что любой из вас помнит, что его первый генератор случайных чисел от a до b выглядел так:
double UniformDiscrete(int a, int b) {
return a + rand() % (b - a + 1);
}
Что ж, это вполне правильное решение.
С единственным и не всегда верным предположением — у вас есть хороший базовый генератор.
Если он неисправен, как старый C rand(), то вы каждый раз будете получать четное число после нечетного.
Если вы не доверяете своему генератору, то лучше написать так: double UniformDiscrete(int a, int b) {
return a + round(BasicRandGenerator() * (b - a) / RAND_MAX);
}
Также следует отметить, что распределение не будет полностью равномерным, если RAND_MAX не будет делиться на длину интервала b - a + 1. Однако разница не будет столь существенной, если эта длина достаточно мала.
Геометрическое распределение
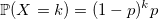

Геометрически распределенная случайная величина с параметром p — это экспоненциально распределенная случайная величина с параметром -ln(1 — p), округленная до ближайшего целого числа.
Доказательство Пусть W — случайная величина, распределенная экспоненциально с параметром -ln(1 - p).
Затем: 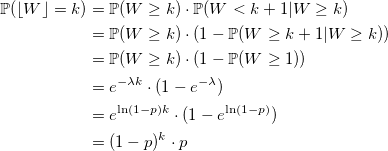
void setupRate(double p) {
rate = -ln(1 - p);
}
double Geometric(double) {
return floor(Exponential(rate));
}
Можно ли это сделать быстрее? Иногда.
Давайте посмотрим на функцию распределения: 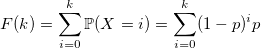
и воспользуемся обычным методом инверсии: генерируем стандартную равномерно распределенную случайную величину U и возвращаем минимальное значение k, при котором эта сумма больше U: double GeometricExponential(double p) {
int k = 0;
double sum = p, prod = p, q = 1 - p;
double U = Uniform(0, 1);
while (U < sum) {
prod *= q;
sum += prod;
++k;
}
return k;
}
Такой последовательный поиск вполне эффективен, учитывая, что значения случайной величины с геометрическим распределением сосредоточены вблизи нуля.
Алгоритм, однако, быстро теряет скорость при слишком малых значениях p, и в этом случае все же лучше использовать экспоненциальный генератор.
Есть секрет. Значения p, (1-p) * p, (1-p)^2 * p,… можно вычислить заранее и запомнить.
Вопрос в том, где остановиться.
И здесь вступает в действие свойство геометрического распределения, которое оно унаследовало от экспоненциального – недостаток памяти: 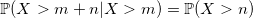
Благодаря этому свойству вы можете запомнить только несколько первых значений (1-p)^i * p, а затем использовать рекурсию: // works nice for p > 0.2 and tableSize = 16
void setupTable(double p) {
table[0] = p;
double prod = p, q = 1 - p;
for (int i = 1; i < tableSize; ++i)
{
prod *= q;
table[i] = table[i - 1] + prod;
}
}
double GeometricTable(double p) {
double U = Uniform(0, 1);
/// handle tail by recursion
if (U > table[tableSize - 1])
return tableSize + GeometricTable(p);
/// handle the main body
int x = 0;
while (U > table[x])
++x;
return x;
}
Биномиальное распределение

По определению случайная величина с биномиальным распределением — это сумма n случайных величин с распределением Бернулли:
double BinomialBernoulli(double p, int n) {
double sum = 0;
for (int i = 0; i != n; ++i)
sum += Bernoulli(p);
return sum;
}
Однако существует линейная зависимость от n, которую необходимо обойти.
Вы можете использовать теорему: если Y_1, Y_2,.
— случайные величины с геометрическим распределением с параметром p, а X — наименьшее целое число, такое, что: 
тогда X имеет биномиальное распределение.
Доказательство По определению, случайная величина с геометрическим распределением Y — это количество экспериментов Бернулли до первого успеха.
Существует альтернативное определение: Z = Y + 1 — количество экспериментов Бернулли до первого успеха включительно.
Это означает, что сумма независимых Z_i представляет собой количество экспериментов Бернулли до X + 1 успеха включительно.
И эта сумма больше n тогда и только тогда, когда среди первых n тестов не более X успешных.
Соответственно: 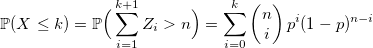
q.e.d.
Время выполнения следующего кода увеличивается только с увеличением значения n * p. double BinomialGeometric(double p, int n) {
double X = -1, sum = 0;
do {
sum += Geometric(p) + 1.0;
++X;
} while (sum <= n);
return X;
}
И все же, временная сложность увеличивается.
Биномиальное распределение имеет одну особенность.
По мере роста n оно стремится к нормальному распределению или, если p ~ 1/n, то к распределению Пуассона.
Имея генераторы этих распределений, они могут заменить в таких случаях генератор бинома.
Но что, если этого недостаточно? В книге Люка Девроя «Неравномерная генерация случайных переменных» есть пример алгоритма, который работает одинаково быстро для любых больших значений n*p. Идея алгоритма заключается в выборке с дисперсией с использованием нормального и экспоненциального распределений.
К сожалению, рассказ о работе этого алгоритма будет слишком длинным для данной статьи, но в указанной книге он подробно описан.
Распределение Пуассона


Если W_i — случайная величина со стандартным экспоненциальным распределением с лямбда-плотностью, то:
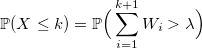
Доказательство Пусть f_k(y) будет плотностью стандартного распределения Эрланга (сумма k стандартных экспоненциально распределенных случайных величин):
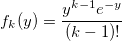
Затем
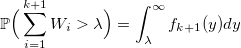
и вероятность получения k:
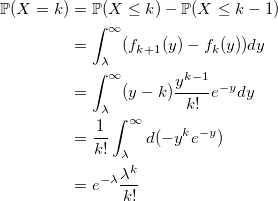
совпадает с распределением Пуассона.
q.e.d.
Используя это свойство, можно написать генератор в виде суммы экспоненциально распределенных величин со степенью плотности: double PoissonExponential(double rate) {
int k = -1;
double s = 0;
do {
s += Exponential(1);
++k;
} while (s < rate);
return k;
}
Популярный алгоритм Кнута основан на том же свойстве.
Вместо суммы показательных переменных, каждая из которых может быть получена обращением через -ln(U), используется произведение равномерных случайных величин: 
а потом: 
Заранее запомнив значение exp(-rate), мы последовательно умножаем U_i до тех пор, пока произведение не превысит его.
void setup(double rate)
expRateInv = exp(-rate);
}
double PoissonKnuth(double) {
double k = 0, prod = Uniform(0, 1);
while (prod > expRateInv) {
prod *= Uniform(0, 1);
++k;
}
return k;
}
Можно использовать генерацию только одной случайной величины и метод инверсии: 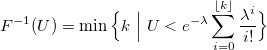
Поиск k, удовлетворяющего этому условию, лучше начинать с наиболее вероятного значения, то есть с Floor(rate).
Сравниваем U с вероятностью того, что X < floor(rate) and go up if U is greater, or down otherwise: void setup(double rate)
floorLambda = floor(rate);
FFloorLambda = F(floorLamda); // P(X < floorLambda)
PFloorLambda = P(floorLambda); // P(X = floorLambda)
}
double PoissonInversion(double) {
double U = Uniform(0,1);
int k = floorLambda;
double s = FFloorLambda, p = PFloorLambda;
if (s < U) {
do {
++k;
p *= lambda / k;
s += p;
} while (s < U);
}
else {
s -= p;
while (s > U) {
p /= lambda / k;
--k;
s -= p;
}
}
return k;
}
Проблема со всеми тремя генераторами одна — их сложность растёт вместе с параметром плотности.
Но есть спасение — при больших значениях плотности распределение Пуассона стремится к нормальному распределению.
Также можно использовать сложный алгоритм из упомянутой выше книги «Неравномерная генерация случайных величин», или просто приблизительный, пренебрегая точностью во имя скорости (в зависимости от того, какая задача).
Отрицательное биномиальное распределение


Отрицательное биномиальное распределение также называют распределением Паскаля (если r является целым числом) и распределением Филда (если r может быть действительным).
Используя характеристическую функцию, легко доказать, что распределение Паскаля представляет собой сумму r геометрически распределенных значений с параметром 1 – p: double Pascal(double p, int r) {
double x = 0;
for (int i = 0; i != r; ++i)
x += Geometric(1 - p);
return x;
}
Проблема такого алгоритма очевидна — линейная зависимость от r. Нам нужно что-то, что будет одинаково хорошо работать в любых условиях.
И отличная недвижимость нам в этом поможет. Если случайная величина X имеет распределение Пуассона: 
где плотность случайна и имеет гамма-распределение: 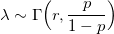
тогда X имеет отрицательное биномиальное распределение.
Поэтому его иногда называют гамма-распределением Пуассона.
Доказательство

Теперь мы можем быстро написать генератор случайных величин с распределением Паскаля для больших значений параметра r. double Pascal(double p, int r) {
return Poisson(Gamma(r, p / (1 - p)));
}
Гипергеометрическое распределение
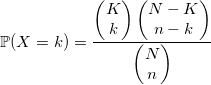
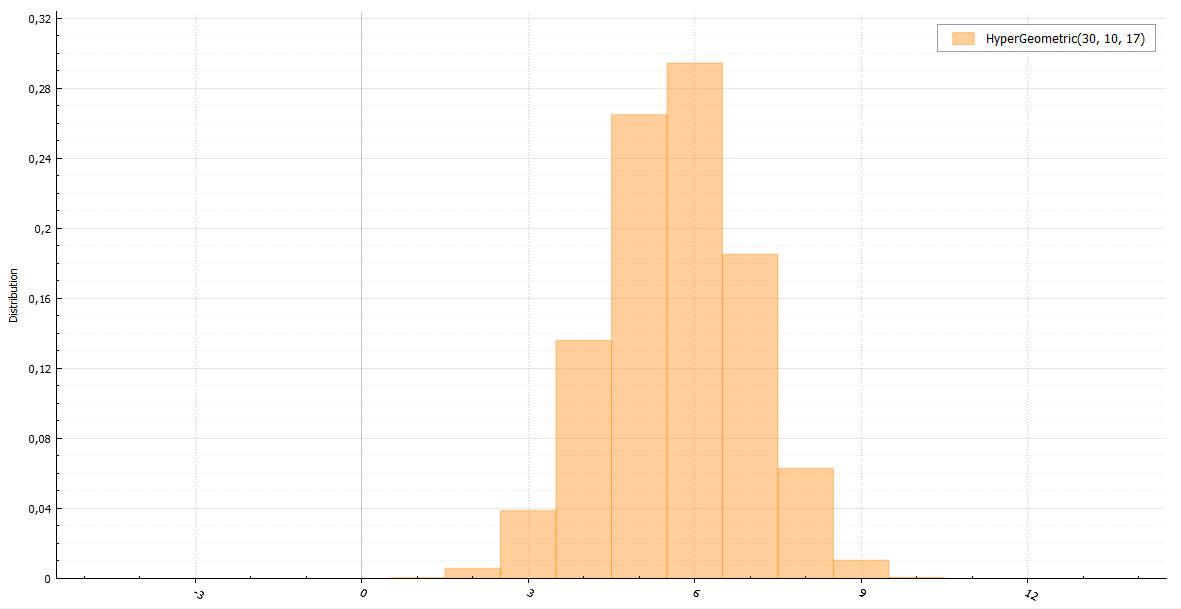
Представьте себе, что в урне N шаров и K из них белые.
Вы рисуете n шаров.
Число белых среди них будет иметь гипергеометрическое распределение.
В общем, лучше использовать алгоритм, использующий это определение: double HyperGeometric(int N, int n, int K) {
double sum = 0, p = static_cast<double>(K) / N;
for (int i = 1; i <= n; ++i)
{
if (Bernoulli(p) && ++sum == K)
return sum;
p = (K - sum) / (N - i);
}
return sum;
}
Или вы можете использовать выборку с отклонением через биномиальное распределение с параметрами: 
и постоянная М: 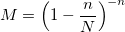
Алгоритм биномиального распределения хорошо работает в крайних случаях больших n и даже больших N (таких, что n << N).
For the rest, it is better to use the previous one, despite its growing complexity with increasing input parameters.
Логарифмическое распределение
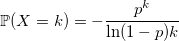
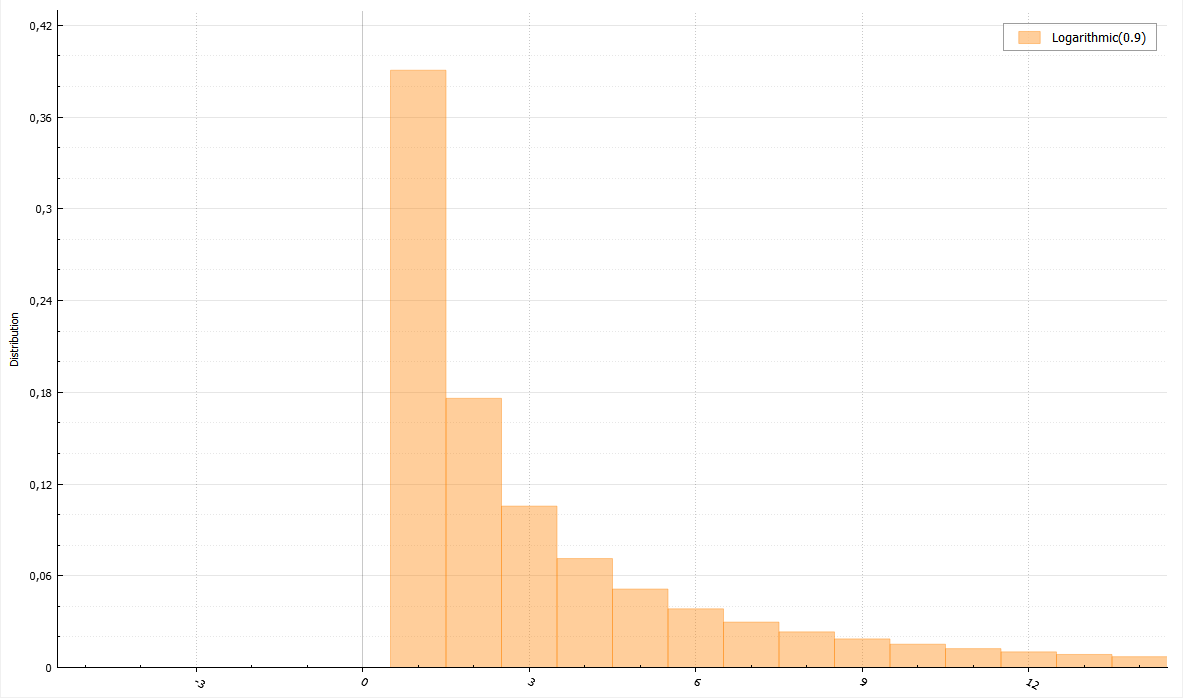
Для этого распределения существует полезная теорема.
Если U и V — равномерно распределенные случайные величины от 0 до 1, то величина 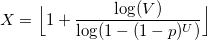
будет иметь логарифмическое распределение.
Доказательство
Вспомнив генераторы экспоненциального и геометрического распределений, легко увидеть, что X, заданный формулой выше, удовлетворяет следующему распределению: 
Докажем, что X имеет логарифмическое распределение: 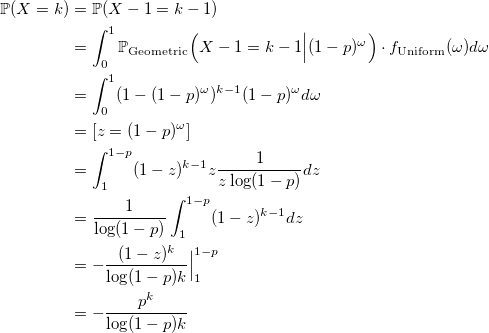
q.e.d.
Чтобы ускорить алгоритм, можно использовать два приема.
Первое: если V > p, то X = 1, поскольку p > = 1-(1-p)^U. Второе: пусть q = 1-(1-p)^U, тогда если V > q, то X = 1, если V > q^2, то X = 2 и т. д. Таким образом можно вернуть наиболее вероятные значения 1 и 2 без необходимости часто считать логарифмы.
void setup(double p) {
logQInv = 1.0 / log(1.0 - p);
}
double Logarithmic(double p) {
double V = Uniform(0, 1);
if (V >= p)
return 1.0;
double U = Uniform(0, 1);
double y = 1.0 - exp(U / logQInv);
if (V > y)
return 1.0;
if (V <= y * y)
return floor(1.0 + log(V) / log(y));
return 2.0;
}
Зета-распределение
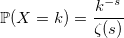
Знаменатель – дзета-функция Римана:

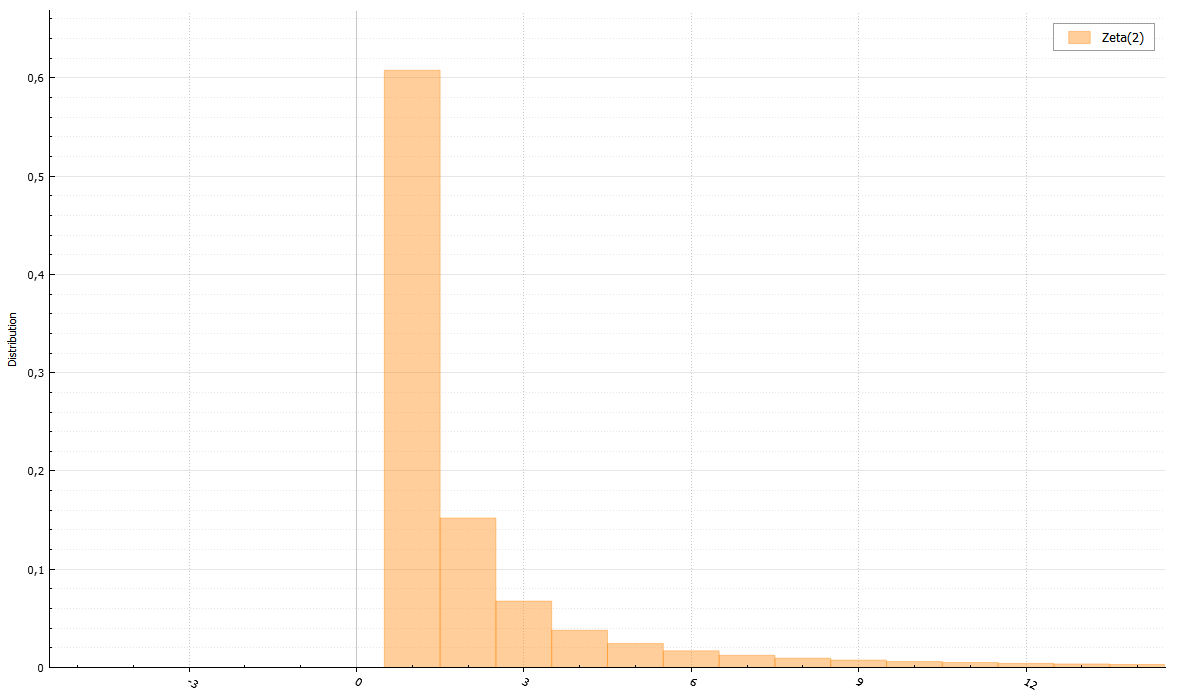
Для дзета-распределения существует алгоритм, позволяющий избежать вычисления дзета-функции Римана.
Вам просто нужно уметь генерировать распределение Парето.
По просьбе читателей могу приложить доказательства.
void setup(double s) {
double sm1 = s - 1.0;
b = 1 - pow(2.0, -sm1);
}
double Zeta(double) {
/// rejection sampling from rounded down Pareto distribution
int iter = 0;
do {
double X = floor(Pareto(sm1, 1.0));
double T = pow(1.0 + 1.0 / X, sm1);
double V = Uniform(0, 1);
if (V * X * (T - 1) <= T * b)
return X;
} while (++iter < 1e9);
return NAN; /// doesn't work
}
Наконец, небольшие алгоритмы для других сложных распределений: double Skellam(double m1, double m2) {
return Poisson(m1) - Poisson(m2);
}
double Planck(double a, double b) {
double G = Gamma(a + 1, 1);
double Z = Zeta(a + 1)
return G / (b * Z);
}
double Yule(double ro) {
double prob = 1.0 / Pareto(ro, 1.0);
return Geometric(prob) + 1;
}
Реализация этих и других генераторов на C++17.
Теги: #случайная величина #генераторы случайных чисел #теория вероятностей #дискретное распределение #случайность не случайна #программирование #Алгоритмы #математика
-
Внимание: Ip В Ит Под Угрозой?
19 Oct, 24 -
Ускоренное Продвижение Java Вперед
19 Oct, 24 -
Реклама На Yahoo Теперь И В России
19 Oct, 24 -
Отчет О Седьмой Киевской Хабравстрече
19 Oct, 24


