В последняя статья мы рассмотрели простейшую линейную генеративную модель PPCA. Вторая генеративная модель, которую мы рассмотрим, — это генеративно-состязательные сети, или сокращенно GAN. В этой статье мы рассмотрим самую базовую версию этой модели, оставив расширенные версии и сравнения с другими подходами генеративного моделирования для последующих глав.

История
Генеративное моделирование включает в себя аппроксимацию невычислимых апостериорных распределений.По этой причине наиболее эффективные методы, предназначенные для обучения дискриминативных моделей, не работают с генеративными моделями.
Предыдущие методы решения этой проблемы сложны в вычислительном отношении и в основном основаны на использовании Марковская цепь Монте-Карло , который плохо масштабируется.
Поэтому для обучения генеративных моделей необходим метод, основанный на масштабируемых методах, таких как Стохастический градиентный спуск (SGD) И обратное распространение ошибки .
Одним из таких методов является генеративно-состязательная сеть (GAN).
GAN были впервые предложены в этом статья в 2014 году.
На высоком уровне эту модель можно описать как две подмодели, которые конкурируют друг с другом, и одна из этих моделей (генератор) пытается научиться в некотором смысле обмануть вторую (дискриминатор).
Для этого генератор генерирует случайные объекты, а дискриминатор пытается отличить эти сгенерированные объекты от реальных объектов из обучающей выборки.
В процессе обучения генератор генерирует объекты, которые всё больше похожи на образец и дискриминатору становится всё сложнее отличить их от реальных.
Таким образом, генератор превращается в генеративную модель, генерирующую объекты из некоторого сложного распределения, например, из распределения фотографий человеческих лиц.
Модель
Для начала введем необходимую терминологию.
Через 
будем обозначать определенное пространство объектов.
Например, картинки 
пиксель.
В некотором вероятностном пространстве 
задана векторная случайная величина 
с распределением вероятностей, имеющим плотность 
такое, что подмножество пространства 
, на которой 
принимает ненулевые значения — это, например, фотографии человеческих лиц.
Нам дан случайный i.i.d. подбор фотографий лиц по размеру 
.
Дополнительно определим вспомогательное пространство 
и случайная величина 
с распределением вероятностей, имеющим плотность 
.

— функция дискриминатора.
Эта функция принимает объект в качестве входных данных 
(в нашем примере изображение соответствующего размера) и возвращает вероятность того, что входное изображение является фотографией человеческого лица.

— функция генератора.
Она принимает смысл 
и производит космический объект 
, то есть в нашем случае картинка.
Предположим, что у нас уже есть идеальный дискриминатор.

.
Для любого примера 
он дает истинную вероятность того, что этот пример принадлежит данному подмножеству 
, из которого была получена выборка 
.
Переформулируя задачу обмана дискриминатора на вероятностном языке, мы находим, что необходимо максимизировать вероятность, порождаемую идеальным дискриминатором на сгенерированных примерах.
Таким образом, оптимальный генератор находится как 
.
Потому что 
является монотонно возрастающей функцией и не меняет положения экстремумов аргумента, перепишем эту формулу в виде 
, что будет удобно в будущем.
В действительности идеального дискриминатора обычно не существует, и его необходимо найти.
Поскольку задачей дискриминатора является подача сигнала для обучения генератора, то вместо идеального дискриминатора достаточно взять дискриминатор, идеально отделяющий реальные примеры от сгенерированных текущим генератором, т.е.
идеальный только на подмножестве 
из которых примеры генерируются текущим генератором.
Эту задачу можно переформулировать как поиск такой функции 
, что максимизирует вероятность правильной классификации примеров как реальных или сгенерированных.
Это называется проблемой бинарной классификации, и в этом случае мы имеем бесконечную обучающую выборку: конечное число реальных примеров и потенциально бесконечное количество сгенерированных примеров.
У каждого примера есть метка: он реальный или сгенерированный.
В первая статья описано решение задачи классификации с использованием метода максимального правдоподобия.
Запишем это для нашего случая.
Итак, наш образец 
.
Определим плотность распределения 
, Затем 
это переформулировка дискриминатора 
, что дает вероятность класса 
(реальный пример) как распределение по классам 
.
Потому что 
, это определение определяет правильную плотность вероятности.
Тогда оптимальный дискриминатор можно найти как: 
Сгруппируем факторы, 
И 
: 


И поскольку размер выборки стремится к бесконечности, мы получаем: 
Итого получаем следующий итерационный процесс:
- Установите произвольный инициал

. - Начинается

-я итерация,
. - Ищем оптимальный дискриминатор для генератора тока:

. - Улучшим генератор, используя оптимальный дискриминатор:

.Важно находиться рядом с генератором тока.
Если отойти далеко от генератора тока, дискриминатор перестанет быть оптимальным и алгоритм перестанет быть корректным.
- Задача обучения генератора считается решенной, если

для всех
.Если процесс не сходится, то переходим к следующей итерации в пункте (2).

Обе функции

можно представить в виде нейронных сетей:

, после чего задача поиска оптимальных функций сводится к задаче оптимизации по параметрам и может быть решена традиционными методами: обратного распространения ошибки и SGD. Кроме того, поскольку нейронная сеть является универсальным аппроксиматором функций,

может аппроксимировать произвольное распределение вероятностей, что устраняет проблему выбора распределения

.
Это может быть любое непрерывное распределение в некоторых разумных пределах.
Например, 
или 
.
Корректность этого алгоритма и сходимость 
К 
при достаточно общих предположениях это было доказано в оригинальной статье.
Нахождение параметров нормального распределения
С математикой мы разобрались, давайте теперь посмотрим, как она работает. Скажем так
, т. е.
решаем одномерную задачу.

.
Давайте воспользуемся линейным генератором 
, Где 
.
Дискриминатором будет полносвязная трехслойная нейронная сеть с бинарным классификатором на конце.
Решение этой проблемы 
, то есть, 
.
Давайте теперь попробуем запрограммировать численное решение этой проблемы с помощью Tensorflow. Полный код можно найти здесь , в статье освещены лишь ключевые моменты.
Первое, что нужно установить, это входной образец: 
.
Поскольку обучение осуществляется с помощью минибатчей, мы будем генерировать вектор чисел за раз.
Кроме того, выборка параметризуется по среднему значению и стандартному отклонению.
Теперь давайте установим случайные входные данные для генератора.def data_batch(hparams): """ Input data are just samples from N(mean, stddev).""" return tf.random_normal( [hparams.batch_size, 1], hparams.input_mean, hparams.input_stddev)

: def generator_input(hparams):
"""
Generator input data are just samples from N(0, 1).
"""
return tf.random_normal([hparams.batch_size, 1], 0., 1.)
Давайте определим генератор.
Возьмем абсолютное значение второго параметра, чтобы придать ему значение стандартного отклонения: def generator(input, hparams):
mean = tf.Variable(tf.constant(0.))
stddev = tf.sqrt(tf.Variable(tf.constant(1.)) ** 2)
return input * stddev + mean
Создадим вектор реальных примеров: generator_input = generator_input(hparams)
generated = generator(generator_input)
И вектор сгенерированных примеров: generator_input = generator_input(hparams)
generated = generator(generator_input)
Теперь давайте прогоним все примеры через дискриминатор.
Здесь важно помнить, что нам нужны не два разных дискриминатора, а один, поэтому нужно попросить Tensorflow использовать одни и те же параметры для обоих входов: with tf.variable_scope("discriminator"):
real_ratings = discriminator(real_input, hparams)
with tf.variable_scope("discriminator", reuse=True):
generated_ratings = discriminator(generated, hparams)
Функция потерь в реальных примерах представляет собой перекрестную энтропию между единицей (ожидаемый ответ дискриминатора в реальных примерах) и оценками дискриминатора: loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.ones_like(real_ratings),
logits=real_ratings))
Функция потерь на поддельных примерах — это перекрестная энтропия между нулем (ожидаемый ответ дискриминатора на поддельных примерах) и оценками дискриминатора: loss_generated = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.zeros_like(generated_ratings),
logits=generated_ratings))
Функция потерь дискриминатора представляет собой сумму потерь на реальных примерах и на поддельных примерах: discriminator_loss = loss_generated + loss_real
Функция потерь генератора — это перекрестная энтропия между единицей (желаемая реакция дискриминатора на поддельные примеры) и оценками дискриминатора этих поддельных примеров: generator_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.ones_like(generated_ratings),
logits=generated_ratings))
К функции потерь дискриминатора дополнительно добавляется регуляризация L2.
Обучение модели сводится к поочередному обучению дискриминатора и генератора в цикле до сходимости: for step in range(args.max_steps):
session.run(model.discriminator_train)
session.run(model.generator_train)
Ниже приведены графики для четырех моделей дискриминаторов:
- трехслойная нейронная сеть.
- трехслойная нейронная сеть с L2-регуляризацией.
- трехслойная нейронная сеть с регуляризацией отсева.
- трехслойная нейронная сеть с L2 и регуляризацией отсева.
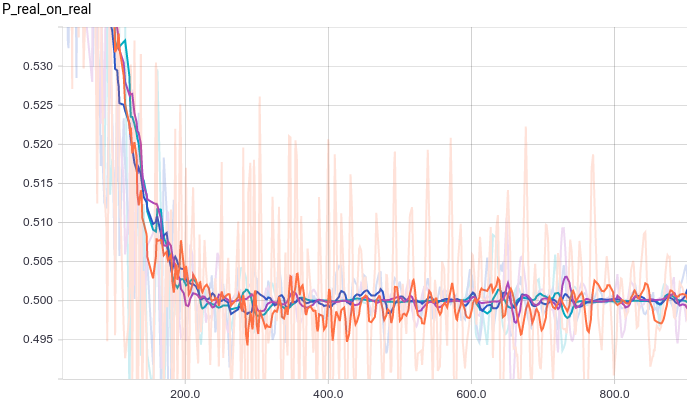
Рис.
1. Вероятность того, что дискриминатор классифицирует реальный пример как реальный.
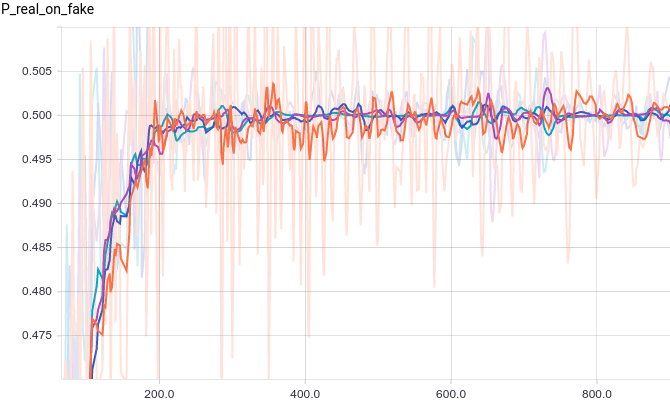
Рис.
2. Вероятность того, что дискриминатор классифицирует сгенерированный пример как реальный.
Все четыре модели быстро сходятся к тому, что выдает дискриминатор.

у всех входов.
Благодаря простоте задачи, которую решает генератор, разницы между моделями практически нет. На графиках видно, что среднее и стандартное отклонение довольно быстро сходятся к значениям из распределения данных: 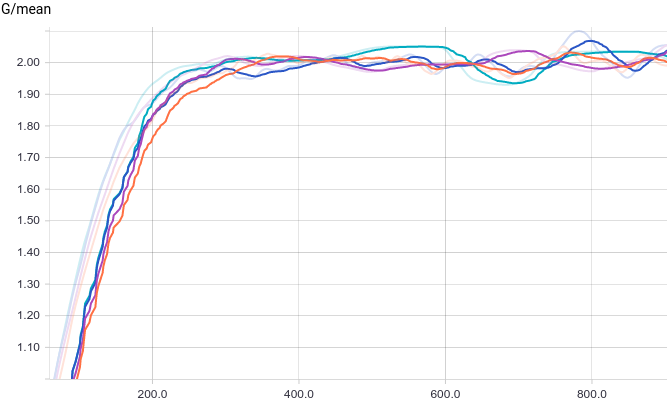
Рис.
3. Среднее сгенерированных распределений.
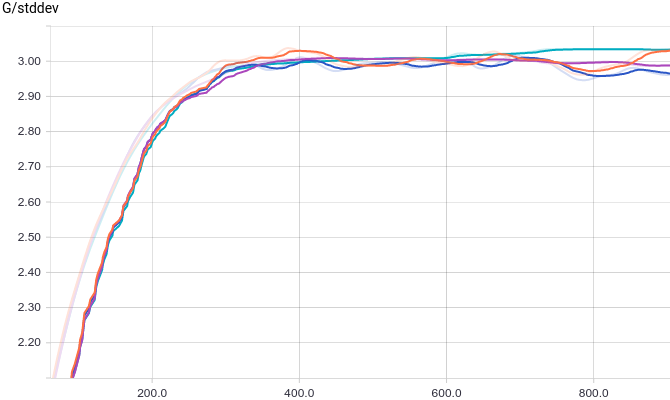
Рис.
4. Стандартное отклонение сгенерированных распределений.
Ниже приведены распределения реальных и сгенерированных в процессе обучения примеров.
Видно, что к концу обучения сгенерированные примеры практически неотличимы от реальных (на графиках они различимы, поскольку Tensorboard выбрал разные масштабы, но если посмотреть на значения, то они одинаковые).
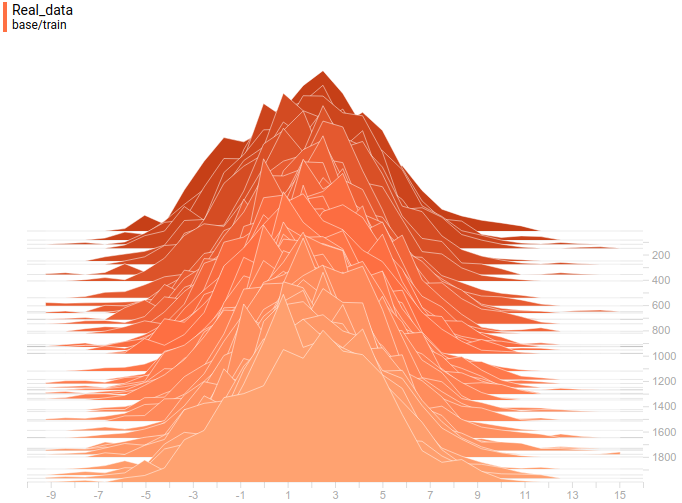
Рис.
5. Распространение реальных данных.
Не меняется со временем.
Шаг обучения отложен на вертикальной оси.
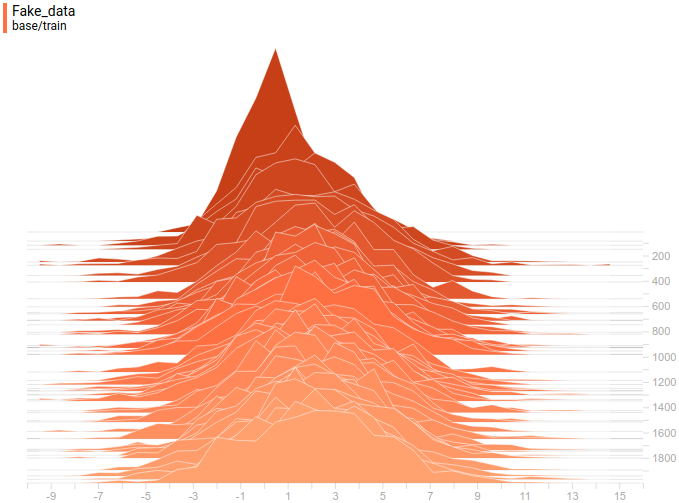
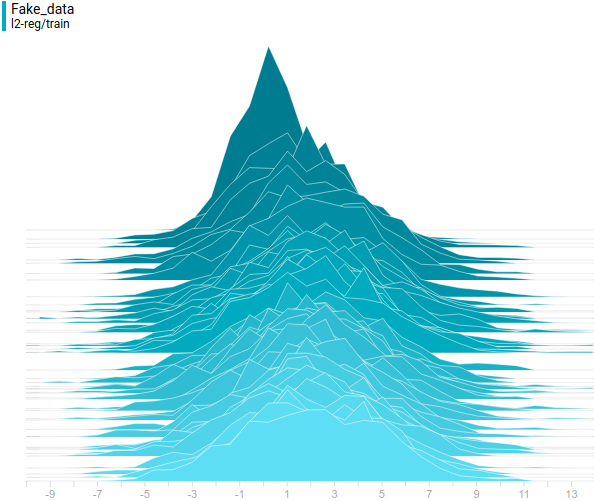
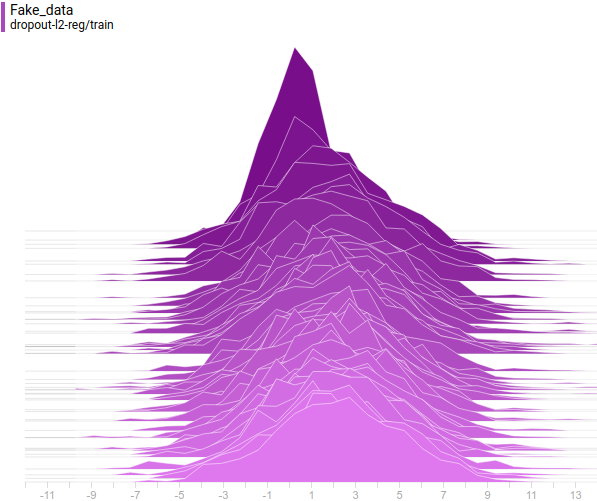
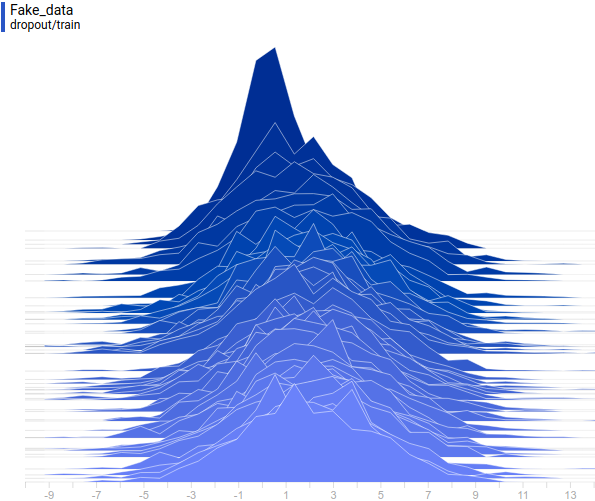
Рис.
6. Распространение реальных данных.
Не меняется со временем.
Шаг обучения отложен на вертикальной оси.
Давайте посмотрим на процесс обучения модели: 
Рис.
7. Визуализация процесса обучения модели.
Стационарная гауссиана — это плотность распределения реальных данных, скользящая гауссиана — это плотность распределения сгенерированных примеров, синяя кривая — результат работы дискриминатора, т.е.
вероятность того, что пример реальный.
Видно, что дискриминатор в начале обучения очень хорошо разделяет данные, но распределение сгенерированных примеров очень быстро буквально «подползает» к распределению реальных примеров.
В конце концов, генератор настолько хорошо аппроксимирует данные, что дискриминатор становится константой.

и проблема сходится.
Аппроксимация смеси нормальных распределений I
Давайте попробуем заменить
на

, тем самым моделируя мультимодальное распределение исходных данных.
Для этой модели вам нужно только изменить код для генерации реальных примеров.
Вместо возврата нормально распределенной случайной величины мы возвращаем смесь нескольких: def data_batch(hparams):
count = len(hparams.input_mean)
componens = []
for i in range(count):
componens.append(
tf.contrib.distributions.Normal(
loc=hparams.input_mean[i],
scale=hparams.input_stddev[i]))
return tf.contrib.distributions.Mixture(
cat=tf.contrib.distributions.Categorical(
probs=[1./count] * count),
components=componens)
.
sample(sample_shape=[hparams.batch_size, 1])
Ниже приведены графики для тех же моделей, что и в последнем эксперименте, но для данных с двумя режимами: 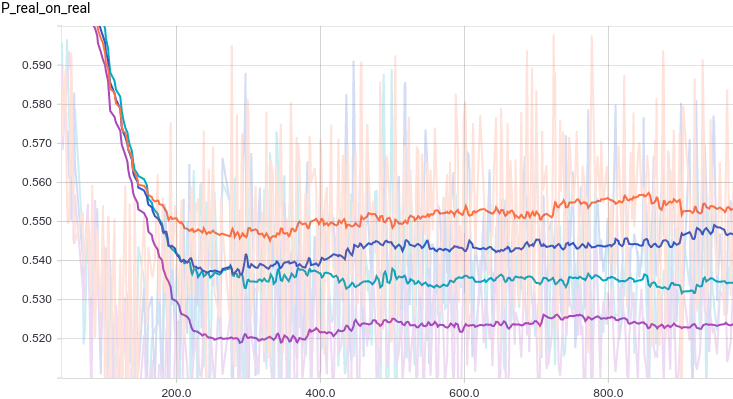
Рис.
8. Вероятность того, что дискриминатор классифицирует реальный пример как повторный.
Теги: #Машинное обучение #теория вероятностей #python #нейронные сети #TensorFlow #программирование #программирование #Алгоритмы #математика #Машинное обучение

-
Яндекс.деньги: Прямая Оплата С Карты
19 Oct, 24 -
Топ-10 Самых Необычных Компьютерных Мышей
19 Oct, 24 -
Преобразование Фурье. Быстрый И Яростный
19 Oct, 24 -
На Чем Ты Сидишь?
19 Oct, 24 -
Как Я Уменьшил Png В 4 Раза
19 Oct, 24 -
Вас Рф: Ип Не Обязаны Вести Кассовую Книгу
19 Oct, 24


