Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.
Теоретическая информация
Давайте рассмотрим математическую теорию.Система линейных уравнений может иметь одно решение, бесконечно много решений или быть несовместной (не иметь решений).
Не все методы решения СЛАУ справляются со вторым случаем, когда система имеет бесконечно много решений.
Например, метод Крамера и матричный метод неприменимы, но можно использовать метод Гаусса.
Алгоритм можно разделить на два этапа:
- Прямой ход
- Обратный ход
На втором этапе неизвестные находятся начиная с конца.
Подробную теорию можно посмотреть по ссылке: Гауссов метод , так что теория пожалуй и всё.
Перейдем к реализации.
Выполнение
Начнем с постановки проблемы:- нам необходимо создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя методы обобщенного программирования.
Система должна содержать коэффициенты производного типа из класса Число (те.
Плавать , Целое число , Двойной и т. д.)
- Запрограммировать алгоритм, который, получив на вход структуру данных системы, формирует нули ниже главной диагонали.
Здесь все должно быть понятно Н какой-то наследник Число 'А, Т — некоторый тип, реализующий заданный интерфейс (рекурсивные дженерики).package gauss; public interface Gauss<N extends Number, T extends Gauss<N, T>> { public void addEquation(T item); public void mul(N coefficient); public N findCoefficient(N a, N b); public N at(int index); public int size(); }
Метод addEquation (элемент T) позволяет добавить каждый элемент уравнения элемент каждому из его элементов.
Остальные методы работают аналогично.
Теперь рассмотрим класс системы уравнений.
Как видно из листинга ниже, он генерируется так же, как интерфейс Gauss, и содержит методы для удобного доступа к частному списку содержащихся уравнений.
package gauss;
import java.util.ArrayList;
import java.util.List;
public class LinearSystem<N extends Number, T extends Gauss<N, T>> {
private List<T> list = new ArrayList<T>();
public T get(int index){
return list.get(index);
}
public void push(T elem){
list.add(elem);
}
public int size(){
return list.size();
}
public N itemAt(int i, int j){
return list.get(i).
at(j);
}
}
Теперь мы можем приступить к реализации «частного случая» структуры уравнения.
Давайте создадим класс MyEquation , который реализует наш интерфейс.
Пусть он будет наследником Число 'и будет сверхточный класс Плавать (на практике лучше брать Двойной ).
Обратите внимание, что в методе addEquation (элемент MyEquation) используется объект класса ListIterator позволяя изменять элементы списка, по которым выполняется итерация.
package gauss;
import java.util.ArrayList;
import java.util.List;
import java.util.ListIterator;
import java.util.Random;
public class MyEquation implements Gauss<Float, MyEquation> {
private List<Float> equation = new ArrayList<Float>();
public List<Float> getEquation(){
return equation;
}
public void generate(int size){
if (size < 2) size = 2;
this.equation.clear();
for (int i = 0; i < size; i++){
Random random = new Random();
this.equation.add((float) (random.nextInt()) + 1);
}
}
@Override
public int size(){
return equation.size();
}
@Override
public void addEquation(MyEquation item){
ListIterator<Float> i = equation.listIterator();
ListIterator<Float> j = item.getEquation().
listIterator();
for(; i.hasNext() && j.hasNext();){
Float a = i.next();
Float b = j.next();
i.set(a + b);
}
}
@Override
public void mul(Float coefficient){
for(ListIterator<Float> i = equation.listIterator(); i.hasNext();){
Float next = i.next();
i.set(next * coefficient);
}
}
@Override
public Float findCoefficient(Float a, Float b){
if (a == 0.0f) return 1.0f;
return -b/a;
}
@Override
public Float at(int index){
return equation.get(index);
}
}
Теперь у нас есть полноценная структура данных, реализующая систему уравнений.
Давайте создадим алгоритм, который будет принимать некоторый объект, реализующий интерфейс Гаусса, затем вызов необходимых методов будет приводить матрицу к нужному виду.
package gauss;
public class Algorithm<N extends Number, T extends Gauss<N, T>> {
LinearSystem<N, T> list = null;
public Algorithm(LinearSystem<N, T> system){
list = system;
}
public void calculate() throws NullPointerException, ArithmeticException{
if (list == null){
throw new NullPointerException("LinearSystem<N, T> instance equal null");
}
if (!checkSystem(list)){
throw new ArithmeticException("Incorrect system for Gauss Method");
}
for(int i = 0; i < list.size() - 1; i++){
for(int j = i + 1; j < list.size(); j++){
N k = list.get(j).
findCoefficient(list.get(j).
at(i), list.get(i).
at(i)); list.get(j).
mul(k); list.get(j).
addEquation(list.get(i)); } } } private boolean checkSystem(LinearSystem<N, T> system){ if (system.size() < 2) return false; for(int i = 0; i < system.size(); i++){ if (system.get(i).
size() != (system.size() + 1)){
return false;
}
}
return true;
}
}
Алгоритм прост: найдите нужный коэффициент, умножьте на него i-ю строку (i=0.n-1) и прибавьте к j-й строке (j=i.n).
Обратите внимание, что алгоритм не знает, как именно реализованы методы.
найтикоэффициент , мул И добавитьEquation , это придает коду большую гибкость, ведь если возникнет необходимость изменить методы манипулирования уравнениями (строками), то будут изменены только реализации трех вышеперечисленных методов, а основной алгоритм останется нетронутым.
Почти все.
Остается только запустить все это в методе основной : import gauss.Algorithm;
import gauss.MyEquation;
import gauss.LinearSystem;
public class Main {
private static final int DEFAULT_EQUATIONS_NUMBER = 2;
private static final int DEFAULT_VARIABLES_NUMBER = 2;
public static void main(String args[]){
LinearSystem<Float, MyEquation> list = generateSystem();
printSystem(list);
int i, j;
Algorithm<Float, MyEquation> alg = new Algorithm<Float, MyEquation>(list);
try{
alg.calculate();
}catch (NullPointerException e){
System.out.println(e.getMessage());
System.exit(0);
}catch (ArithmeticException e){
System.out.println(e.getMessage());
System.exit(0);
}
Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER];
for(i = list.size() - 1; i >= 0; i--) {
Float sum = 0.0f;
for(j = list.size() - 1; j > i; j--) {
sum += list.itemAt(i, j) * x[j];
}
x[i] = (list.itemAt(i, list.size()) - sum) / list.itemAt(i, j);
}
printSystem(list);
printVector(x);
}
public static LinearSystem<Float, MyEquation> generateSystem(){
LinearSystem<Float, MyEquation> list = new LinearSystem<Float, MyEquation>();
int i;
for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++){
MyEquation eq = new MyEquation();
eq.generate(DEFAULT_VARIABLES_NUMBER + 1);
list.push(eq);
}
return list;
}
public static void printSystem(LinearSystem<Float, MyEquation> system){
for (int i = 0; i < system.size(); i++){
MyEquation temp = system.get(i);
String s = "";
for (int j = 0; j < temp.size(); j++){
s += String.format("%f; %s", system.itemAt(i, j), "\t");
}
System.out.println(s);
}System.out.println("");
}
public static void printVector(Float [] x){
String s = "";
for (int i = 0; i < x.length; i++){
s += String.format("x%d = %f; ", i, x[i]);
}System.out.println(s);
}
}
Давайте запустим это чудо и проверим, корректно ли оно работает. 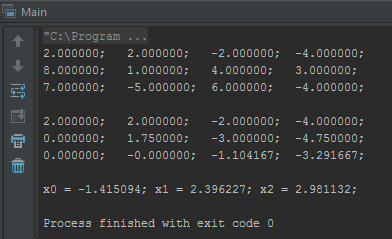
Это все.
Источники можно скачать на github.
Заключение
Метод Гаусса не очень поддается обобщенному программированию (как видите, обратный ход делается отдельно), но получилась уникальная реализация, которая, надеюсь, поможет кому-то лучше понять искусство использования интерфейсов и дженериков.
Список использованной литературы:
- Математика доступным языком.
метод Гаусса
- Википедия.
метод Гаусса
- Ээквивалентные матричные преобразования

-
Повышение Рейтинга В Поисковых Системах
19 Oct, 24 -
Firefox 3 Бета 2
19 Oct, 24


