После прочтения статьи «Динамическая система Лоренца и вычислительный эксперимент» , проверил расчеты аналитико-численным методом [1].
Результаты расчета на фазовой плоскости z(x): 
И у(х): 
Кажется, что кривые замкнуты, но давайте посмотрим на результат подробнее.
Коротко об используемом методе расчета Аналитико-численный метод относится к самозапускающимся непрерывным методам переменного порядка с адаптивной процедурой выбора шага и с контролем уровней ограничения абсолютных локальных и суммарных погрешностей расчета.
Он используется для решения обычных нелинейных неавтономных нестационарных интегродифференциальных уравнений, описывающих динамические модели систем, находящихся под детерминированными воздействиями.
При расчете регулярная составляющая искомого решения представляется в виде ряда Тейлора.
Результатом применения аналитико-численного метода при решении систем ОДУ, описывающих модель динамической системы, являются не только приближенные решения, но и области, гарантированно содержащие точные решения.
То есть, помимо самого численного значения приближенного решения, в результате получаются и верхние оценки максимальной суммарной ошибки расчета на каждом шаге расчета: 
Где 
— приближенное решение (i-я фазовая координата); 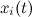
— неизвестно точное решение; 
— верхняя оценка максимальной суммарной ошибки вычисления приближенного решения;
Параметры для расчета взяв из статьи «Динамическая система Лоренца и вычислительный эксперимент» :
Начальные условия, параметры динамической системы, точность математических операций - 180 знаков после запятой, точность в степенном ряду 1е-9, в точке t=6,827 получаем следующий результат: 
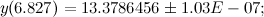

Производные значения: 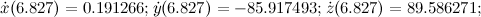
Нетрудно заметить, что результаты расчетов несколько отличаются от представленных в статье.
Кроме того, если подставить результат из статьи (найденные приближенные значения решений) в исходную систему уравнений, то получим значения производных, также отличающиеся от указанных в статье: 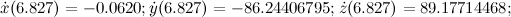
Замечу, что повышение точности вычислений (количества учитываемых десятичных знаков и точности степенного ряда) приводит лишь к сужению области, содержащей точные решения.
Например, при установке точности 1e-55 область при t = 6,827 сужается до 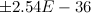
.
Далее я решил продолжить расчет до точки t = 12,827 и рассмотреть график результатов расчета на фазовых плоскостях z(x): 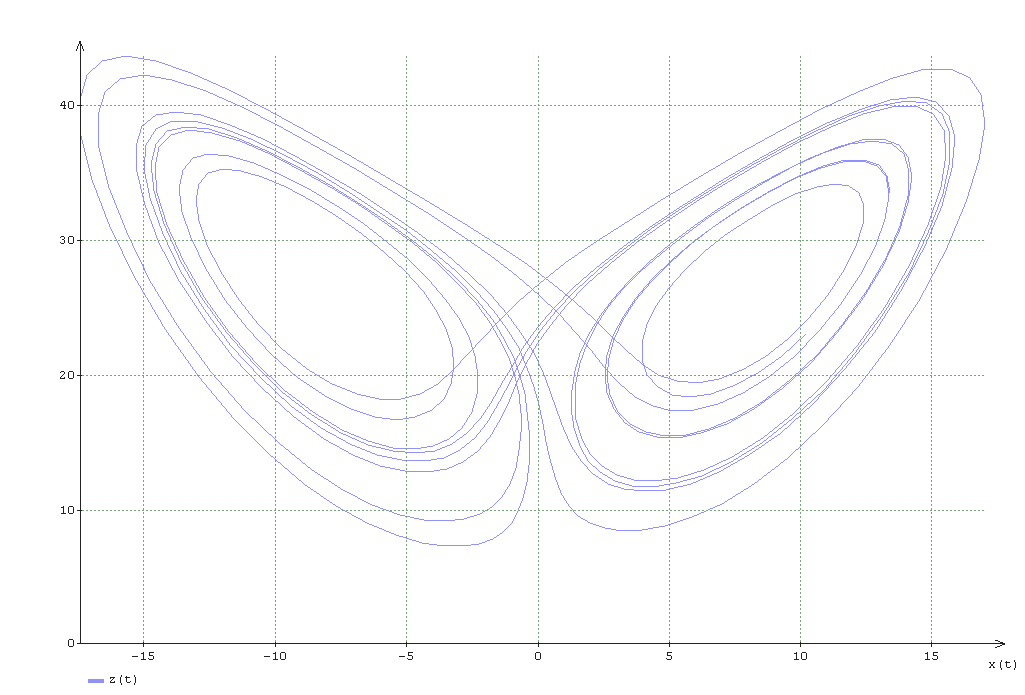
И у(х): 
На графиках ясно видно, что кривые не замкнуты.
Если быть еще точнее, на первых графиках они не замкнуты, просто масштаб, в котором отображены фазовые траектории, не позволяет увидеть точку открытости.
Таким образом, ни о каком возврате траектории в окрестности начальной точки говорить не приходится – об этом говорится в статье.
И всегда необходимо делать выводы на основе расчетов с учетом погрешностей расчетов (как методических, так и расчетных).
Литература: 1. Бычков Ю.
, Щербаков С.
Аналитико-численный метод расчета динамических систем.
- СПб.
: Энергоатомиздат, 2001. Теги: #аттрактор #аттрактор Лоренца #степенной ряд #численные методы #высокоточные расчеты #система Лоренца #математика

-
Как Очистить Реестр Компьютера?
19 Oct, 24 -
Секреты Тестирования Интерфейсов В Ткс Банке
19 Oct, 24 -
Уничтожение Данных На Жестком Диске
19 Oct, 24 -
Классификатор На Word2Vec
19 Oct, 24 -
Цифровая Подпись И Электронные Закупки
19 Oct, 24 -
Спам В Блогах Меняет Цели И Тактику
19 Oct, 24 -
Opengl Против Directx, Эпизод Ii
19 Oct, 24


