Часть 0: Фракталы в простых числах.
Часть 1: Фракталы в иррациональных числах.

В статье присутствуют Gif и контрастные картинки.
У эпилептиков может случиться эпилептический припадок.
В предыдущей статье мы рассмотрели алгоритм визуализации двоичных последовательностей.
Давайте вспомним.
Возьмем двоичную последовательность.
В качестве примера, первые несколько битов фрактальной последовательности, обсуждавшейся в предыдущей статье:
0100110110010011001001101100
Нарисуйте квадратное поле ячеек.
Располагаем биты по верхней границе.
Расстояние между битами — две ячейки: 
Для каждого бита нарисуйте пунктирный путь по диагонали (через ячейку).
Для нулей нарисуйте первую черту вправо: 
Для единиц – слева: 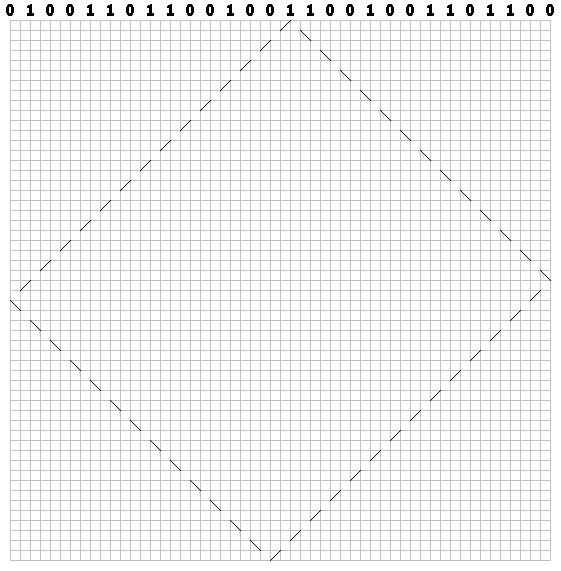
Мы нарисовали траекторию для каждого бита.
У нас получился «бильярдный» узор: 
Идентичный узор (без дефекта по диагонали — последовательность бесконечна, но мы визуализировали ее как конечную последовательность) можно получить и другим способом.
Мы инвертируем каждый четный бит в последовательности:
0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1
Далее для каждого бита рисуем вертикальные пунктирные линии: 
Располагаем биты слева, рисуем горизонтальные линии:
Мы совмещаем: 
После написания первой статьи нерешёнными остались два вопроса:
1. Можно ли нарисовать фрактальную картину иррациональных чисел.
Может. Вопрос решен в предыдущей статье.
Изображение выше является частью фрактального узора для
.
Если вы выберете одну из кривых в этом шаблоне: 
Получаем всем известную фрактальную кривую – «фрактал слова Фибоначчи».
2. Второй вопрос: можно ли написать алгоритм, рисующий узор: 
В этой статье мы рассмотрим второй вопрос.
Раскрашивать узоры мы будем с помощью ткацкого станка, работа которого будет моделироваться с помощью JavaScript. 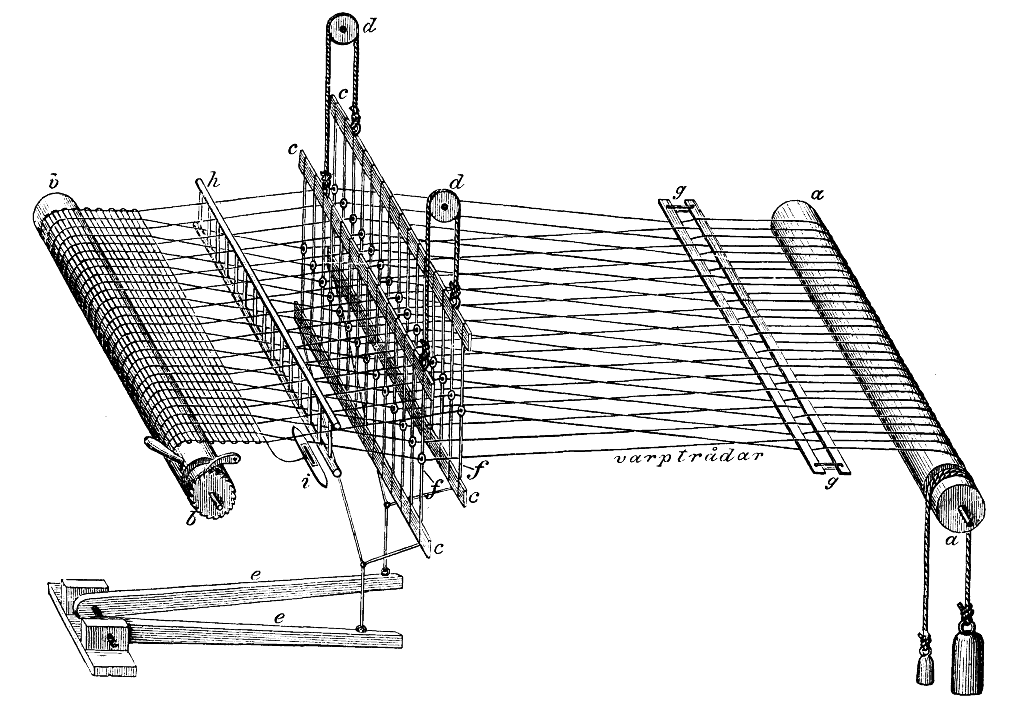
На схеме выше показана простейшая машина.
Он состоит из двух рамок, через которые протягиваются нити.
Рамы соединены с педалями.
При нажатии на одну из педалей одна из рамок поднимается.
Нити, протянутые через этот каркас, поднимаются и в образовавшийся зазор между нитями втягивается поперечная нить.
Если четные и нечетные нити протянуть через разные рамки, получится шахматное переплетение: 
Более сложные машины используют четыре и более фреймов: 
Настольный ткацкий станок Ashford с 4 валами
Чтобы не запутаться, какую педаль нажимать, составляют схему.
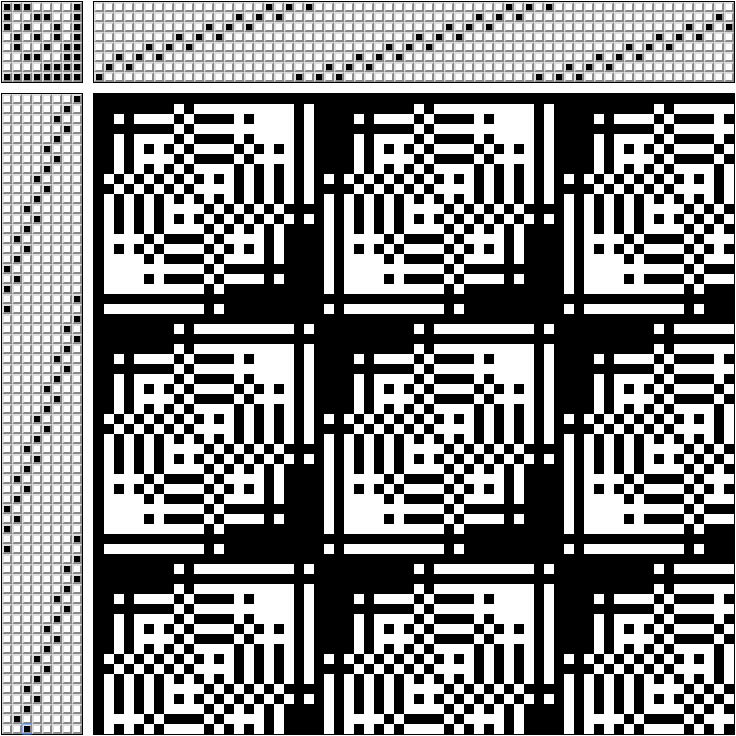
В правой верхней части схемы отмечено, через какие рамки проходят нити (схема для ткацкого станка на 8 рамок).
В левом верхнем углу - какие педали одновременно нажимать (каждая педаль связана только со своей рамкой).
В левой нижней части - в каком порядке нажимать педали.
В правой нижней части – какое плетение у нас получится.
Если протянуть белую нить через черные, получится монохромный узор.
Сразу «переезд» может показаться немного сложным.
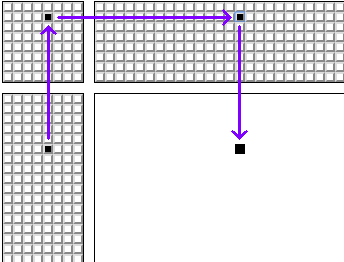
На рисунке ниже показано, как формируется схема плетения: 
Давайте напишем сценарий.
Мы будем протягивать нити через рамки с помощью одномерного массива array2. Запишем порядок нажатия педалей в одномерный массив array1. В массиве3 (двоичный массив 8х8) мы запишем, какие педали нажимать одновременно.
Теги: #математика #Алгоритмы #JavaScript #Визуализация данных #Аномальное программирование #фракталы #хаос #иррациональные числа #синергетика #математический бильярд

-
Анатомия Кроссовок Asics
19 Oct, 24 -
С Чего Начать Свой Покерный Блог?
19 Oct, 24 -
Дайджест Laravel (6–13 Декабря 2020 Г.)
19 Oct, 24 -
Вышла Ios 6.0.1
19 Oct, 24 -
Трансляция С «Поговорим» На Iphone
19 Oct, 24 -
Самый Ужасный Код В Моей Жизни
19 Oct, 24 -
Замена Д-Линка
19 Oct, 24


