Статья адресована и будет полезна в первую очередь тем, кто начал изучать варианты и хочет разобраться в их ценообразовании.
Ну, а во-вторых, для тех, кто еще не использует инструмент VBA в своих расчетах в Excel, но хочет научиться – вы увидите, насколько это на самом деле просто.
Основы опций
Для начала кратко поговорим о сути и ценах опций.Опция имеет четыре основных параметра: 1. Базовый актив 2. Тип опции (колл или пут) 3. Страйк-цена (цена исполнения опциона) 4. Дата окончания срока (истечение) опциона Для покупателя опциона он представляет собой право купить (опцион колл) или продать (опцион пут) базовый актив по цене исполнения на дату истечения срока действия.
Для продавца опциона он представляет собой обязательство продать (опцион колл) или купить (опцион пут) базовый актив по цене исполнения в день истечения срока действия.
По сути, опцион представляет собой страхование от изменения цены базового актива (БА) с момента заключения сделки до даты экспирации - страховщиком (в случае неблагоприятного изменения цены БА) выступает продавец.
, он платит страховку покупателю опциона), а страховщик является покупателем опциона (он платит за страховку продавцу).
Как и цена страхования, цена опциона полностью определяется вероятностью «страхового случая», т.е.
реализации опциона (реализации права покупателя опциона).
Основные составляющие, влияющие на эту вероятность и цену опциона, стоимость страховки, которую платит покупатель и получает продавец:
- Разница между ценой исполнения и ценой базового актива .
Те.
при покупке Call, чем выше его страйк, тем он дешевле (поскольку снижается вероятность того, что в момент экспирации BA будет выше страйка)
- Волатильность базовый актив.
Чем выше волатильность (примерно диапазон ценовых колебаний) БА, тем выше вероятность достижения страйка до истечения срока действия.
- Время до истечения срока действия .
Чем дольше время до истечения срока действия опциона, тем выше вероятность того, что при покупке Колла цена базового актива за это время поднимется выше страйка, и соответственно цена опциона будет выше.
Общепринятая ныне формула оценки опционов, основанная на этих базовых факторах, была разработана Фишером Блэком и Майроном Шоулзом в 1973 году.
Формула Блэка-Шоулза имеет следующий вид (подробности можно найти в Википедии):
(Европейская) цена опциона колл: 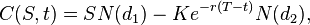
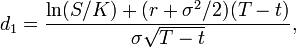

(Европейская) цена опциона пут: 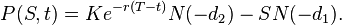
Обозначения: С(S,t) — текущая стоимость опциона колл в момент времени t до истечения срока действия опциона (до истечения срока действия); С — текущая цена базового актива; Н(х) — вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (ограничивая тем самым диапазон значений функции стандартного нормального распределения); К — цена исполнения опциона; р — безрисковая процентная ставка; Т - т — время до истечения срока действия опциона; 
— волатильность доходности (квадратный корень из дисперсии) базового актива.
Греки вариантов
Для оценки чувствительности цены опциона к цене БА, волатильности и времени до экспирации используются коэффициенты, называемые греками (коэффициенты обычно обозначаются греческими буквами, за исключением «веги»).
Греки в модели Блэка-Шоулза рассчитываются следующим образом:
1. Дельта ( 
) — скорость изменения цены опциона в зависимости от изменения цены БА.
Для опциона колл дельта равна 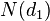
, для опциона пут 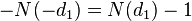
.
Дельта показывает текущий наклон кривой стоимости опциона в зависимости от цены БА.
2. Гамма ( 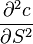
) — скорость изменения цены опциона от изменения Дельты (или ускорение от изменения цены БА).
Гамма равна 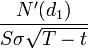
.
3. Вега ( 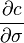
) — описывает зависимость цены опциона от изменения волатильности БА: 
.
Вега отражает количество пунктов изменения стоимости опциона на каждый процентный пункт (1%) изменения волатильности.
4. Тета ( 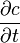
) — описывает снижение цены опциона в зависимости от времени до экспирации.
Для звонка - 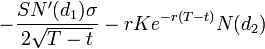
, для Пута - 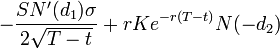
.
Приведенные выше формулы справедливы для общего случая, включая случай опционов на акции.
Безрисковая ставка r не используется для расчета опционов на фьючерсные контракты.
Потому что опционы на фьючерсы торгуются на Московской бирже; дальнейшие расчеты не учитывают процентную ставку.
Реализация модели в MS Excel
Итак, реализация модели Блэка-Шоулза в Excel+VBA. Для удобства создадим функцию для каждой переменной из модели BS. Каждая функция будет иметь входные переменные: S — цена БА X - цена исполнения d — количество дней до истечения срока действия у - количество дней в году v - волатильность OptionType - тип опциона «Колл» или «Пут» (только для расчета цены и дельты) Написание обычной функции в VBA выглядит так:Функция Имя функции (входные переменные, разделенные запятыми) .Такую функцию можно вызвать как из других функций, так и из листа Excel. Функции записываются в созданный Модуль (запустите VBA в Excel, например, нажав Alt+F11, выберите Вставить -> Модуль):расчеты.
Имя функции =.
вычисления.
Конечная функция
Функция d_1(S, X, d, y, v) Т=д/г d_1 = (Log(S / X) + (0,5 * (v^2)) * T) / (v * (T^0,5)) Конечная функция Функция d_2(S, X, d, y, v) Т=д/год d_2 = d_1(S, X, d, y, v) - v * (T ^ 0,5) Конечная функция Функция Nd_1(S, X, d, y, v) Nd_1 = Application.NormSDist(d_1(S, X, d, y, v)) Конечная функция Функция Nd_2(S, X, d, y, v) Nd_2 = Application.NormSDist(d_2(S, X, d, y, v)) Конечная функция Функция N_d_1(S, X, d, y, v) N_d_1 = Application.NormSDist(-d_1(S, X, d, y, v)) Конечная функция Функция N_d_2(S, X, d, y, v) N_d_2 = Application.NormSDist(-d_2(S, X, d, y, v)) Конечная функция Функция N1d_1(S, X, d, y, v) Т=д/год N1d_1 = 1/(2 * Application.Pi()) ^ 0,5 * (Exp(-0,5 * d_1(S, X, d, y, v) ^ 2)) Конечная функция Функция OptionPrice(OptionType, S, X, d, y, v) Если OptionType = «Вызов» Тогда OptionPrice = S * Nd_1(S, X, d, y, v) - X * Nd_2(S, X, d, y, v) ИначеЕсли OptionType = «Поставить» Тогда OptionPrice = X * N_d_2(S, X, d, y, v) — S * N_d_1(S, X, d, y, v) Конец, если Конечная функция Функция Дельта (OptionType, S, X, d, y, v) Если OptionType = «Вызов» Тогда Дельта = Application.NormSDist(d_1(S, X, d, y, v)) ИначеЕсли OptionType = «Поставить» Тогда Дельта = Application.NormSDist(d_1(S, X, d, y, v)) - 1 Конец, если Конечная функция Функция Тета(S, X, d, y, v) Т=д/год Тета = -((S * v * N1d_1(S, X, d, y, v)) / (2 * (T^0,5))) / y Конечная функция Функция Гамма(S, X, d, y, v) Т=д/год Гамма = N1d_1(S, X, d, y, v) / (S * (v * (T^0,5))) Конечная функция Функция Вега(S, X, d, y, v) Т=д/год Вега = (S * (T^0,5) * N1d_1(S, X, d, y, v)) / 100 Конечная функцияГотовый файл Excel можно скачать с сайта связь .
Теперь в ячейке Excel мы можем вызвать любую написанную нами функцию, например, введя в ячейку =OptionPrice("Put";76870;90000;13;365;0,47) мы получим теоретическую цену опциона Put при цена базового актива 76870, страйк 90000, ожидаемая волатильность 45% и 13 дней до экспирации.
Некоторые моменты, которые хотелось бы отметить
- Теоретические значения цен, полученные в нашей программе, практически идентичны транслируемым Московской биржей, а это означает, что биржа в своих расчетах использует модель BS.
- На самом деле опцион (как и страховка) не имеет истинной справедливой стоимости – она у всех разная, и зависит от того, какая волатильность ожидается или, например, какое количество дней учитывать (учитывать ли выходные дни).
, с каким весом учитывать разные дни недели, сколько дней в году использовать в формуле) и т.д.
- У греков есть замечательное свойство: чтобы получить греческую стоимость портфеля фьючерсов и опционов, вы просто добавляете соответствующие греки для отдельных активов портфеля.
Те.
мы можем легко подсчитать, например, сколько базовых фьючерсов необходимо купить/продать, чтобы общая стоимость портфеля не менялась при изменении цены этого фьючерса (так называемое дельта-выравнивание или дельта-хеджирование).
- Несмотря на свою распространенность, модель BS основана на предположении, что доходность актива имеет нормальное распределение, что никогда не бывает верным на реальном рынке.
Нижняя граница
Итак, мы получили работающий калькулятор опционов на VBA, который можно использовать как для изучения свойств опционов (построить диаграммы зависимости цен и греков от различных параметров рынка), так и использовать для торговли и построения более сложных программ.Теги: #опции #финансы #Excel #vba #программирование #математика #Visual Basic для приложений
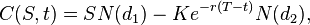
-
Ozon Изнутри: Похоже На Стартап
19 Oct, 24 -
Карантин В Чехии: Взгляд Изнутри
19 Oct, 24 -
7 Вопросов О Компьютерной Томографии
19 Oct, 24 -
Лучший Сотрудник Месяца
19 Oct, 24 -
Эти Часы Пишут Время...
19 Oct, 24


