Боже мой, часть четвёртая! Это выше моих сил! Успокойтесь, у меня заканчиваются таблетки, так что это последняя статья, и в ней будут откровения.
Под катом описание процесса примерки, подтяжки ушей, запутывания и манипуляций.
В предыдущем ( 1 , 2 , 3 ) частей мы видели, как разные пропорции использовались в геометрии, древнем искусстве и современном промышленном дизайне.
Мы оставили неразгаданной тему золотого сечения и еще один корень – √5. Давайте начнем.
Однажды люди столкнулись с идеей пропорций.
Одни и те же закономерности постоянно встречались на различных фигурах.
Это было впечатляюще.
Тогда кто-то додумался измерить пару растений, животных и некоторые части тела, которые обычно скрыты от посторонних.
Там тоже были закономерности.
Это было еще более впечатляюще.
Терпения больше не осталось; самые обычные отношения были объявлены священными.
Некоторые видели в них проявление божественного вмешательства.
Некоторые – сам Бог.
А поскольку сакральные пропорции встречаются так часто, к ним можно подогнать все, что угодно, сделать из этого символ и напугать свою паству.
Мистификации и приписки с лучшими намерениями постоянно встречаются в истории.
Например, переписчики классического труда Беды Достопочтенного «Церковная история народа англов» добавляли в текст куски, чтобы отдельные церковные вопросы выглядели более выгодно.
А главы 25-28 VI книги Цезаря «Записки о Галльской войне», видимо, не такие Цезаревские.
То же самое касается и символизма.
Людям необходимо почувствовать ее глубокий смысл, а сама форма не столь важна.
Возьмите любую фотографию, вы обязательно что-то в ней найдете.
Чем старше, тем лучше.
Самая древняя наша страна – Египет, потренируемся на нем.
Вот схема барельефа из гробницы Петосириса, найденной в 1919 году.

Проведя достаточно времени с линейкой и циркулем, можно найти в ней золотое сечение и кучу других связей (кроме текста букв, шуток, для этого компас не понадобится).

Это выглядит настолько круто, что нет оснований не сказать, что египтяне знали о золотом сечении и делали это намеренно.
Мистифицировать геометрию легко и просто.
Сейчас я покажу вам пару техник.
Посмотрите под катом.
Итак, хитрости.
Ну, во-первых, все эти пропорции настолько древние, что все самые крутые конструкции хорошо описаны.
Открыв справочник, мы видим, как самым простым способом заставить те самые золотые пропорции прогреметь.
Возьмите квадрат, нарисуйте его один конец и нарисуйте диагональ АС.

Постройте круг с центром О и радиусом ОА.
Продлите линию FE до точки пересечения с окружностью К.
Затем можно повторить трюк с окружностью для стороны АВ, но проще провести перпендикуляр КН из К, продлить АВ и отметить точку пересечения Н.

Вуаля, у нас есть «золотой прямоугольник».
Отношение FE к EK такое же, как FK к FE. Что еще более удивительно, так это то, что KF/FB тоже соответствует этому.
Для краткости греки называли это соотношение φ (Фи).
Оно примерно равно 1,618. Давайте проявим творческий подход и сделаем еще пару проходов.
Соедините углы исходного квадрата и получившегося прямоугольника.
Нарисуем круг по образовавшимся точкам.

Теперь, чтобы приоткрыть завесу великой тайны, нам нужно найти то, что умещается в этот прямоугольник.
Вспомнив, как нам повезло с Apple, давайте пойдем самым простым путем и сделаем очевидное.

Ура! Нам удалось объявить iPod 4G священным устройством.
Совершенно очевидно, что теперь его обязательно купят. В этом польза изучения учебников.
Геометрия существует так долго, что ничего не стоит брать справочники и классические источники, писать книги и зарабатывать на этом большую прибыль.

Смотрите, книгу будут снимать с каким-нибудь актером, который выглядит ошарашенным сценарием, и прибыль будет еще больше.
Можно компостировать мозг читателя, а можно компостировать мозг читателя так же, как можно компостировать мозг читателя - тоже, кстати, выгодно (ну вы понимаете, о чем я, мои начитанные комментаторы).
По крайней мере, можно удивить современников и заработать некоторые преимущества, разгадав тайны арабской мозаики, соединив ее.
ну, скажем, с пчелой.

На самом деле в искусстве, конечно, все дело в обычных модульных сетках и ведущих линиях, которые художники и дизайнеры используют для составления композиций.
Идея настолько стара, что ею пользовались даже самые древние из древних египтян.
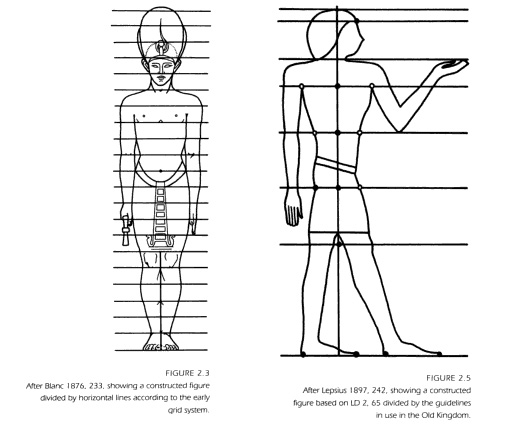
Композицию преподают в художественных школах, и тех, кто преподает, тоже кто-то когда-то преподавал.
Так что никакой мистики.
Разве что только самый первый учитель что-то там придумал.
В остальном достаточно взять какую-нибудь сетку и расположить на ней элементы.
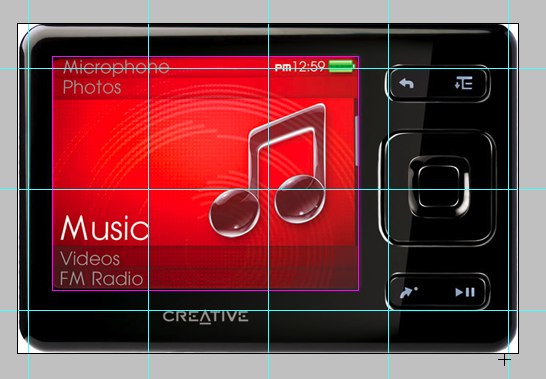
А вот полуторное соотношение сторон и квадратные модули не интересны.
Никакого секрета.
Лучше взять что-то более «святое».
Допустим, еще одно известное соотношение — √5. Плеер Zune делает именно это.

Давайте заглянем в справочник и посмотрим, какие закономерности могут возникнуть.

Давайте поместим их на плеер.
Хм.
Ничего подобного пока нет. Попробуем рассмотреть все варианты.
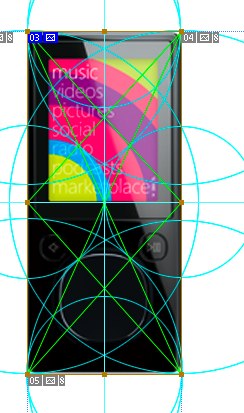
Эммм.
Тухло как-то.
Единственное, что интересно — это касания возле центральной кнопки.
Тогда мы поиграем с 4it. Давайте возьмем линейку, измерим размеры элементов и попробуем найти разделители.

Объясняет саркоидоз и агрессивное поведение.
блин, кажется, я пишу не через то окно.
В общем, здесь снова унылые квадраты, которые мало кого смутят. Они испортили такое хорошее начало.
Нам придется снова вернуться к iPod. iPod Nano 2G также имеет соотношение сторон √5/1. Давайте еще раз посмотрим на схему из справочника и подумаем, как ее к чему-нибудь приклеить.
Ага.
Есть сторона √5, которую можно втиснуть в предыдущую конструкцию.

Из точек А, О и С проведем дуги радиусом AB (так как для нас это 1x, а AC — √5x).
Из этих же точек проводим перпендикуляры к AC до тех пор, пока они не пересекутся с дугами.
Соединим новые пересечения и вот наш iPod почти готов.

Ахалай, махалай, абра-кадабра! 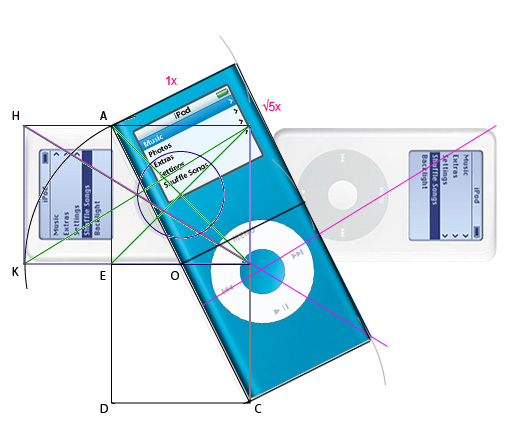
Итак, что мы узнали?
1. Если вы хотите запутать людям головы, всегда следует использовать мистические числа √2, √3, √5 и φ.
С ними всегда будут самые «загадочные» совпадения.
Есть еще много интересных вещей, таких как последовательности Фибоначчи, спирали, гномические увеличения и всякие хитрые деления.
Но чем проще, тем легче всех запутать, правда? 

2. Apple определенно промывает людям мозги.
Ведь у них есть целый набор молодых оккультистов: 
3. Из простого квадрата можно сконструировать целый взрыв мозга, религию, алгебру, дихотомию добра и зла.

Здесь каждый увидит то, что хочет, включая сиськи и Микки Мауса (если интересно, вы также можете увидеть Звезду Давида).
Человеку свойственно искажать простые идеи.
Но вот тут-то все и началось: 
Теги: #дизайн #философия #геометрия #математика

-
Как Сделать Картриджи Источником Экономии
19 Oct, 24 -
«Частное Решение Проблем Человечества»
19 Oct, 24 -
Менеджеры И Супервайзеры. Ищем Различия
19 Oct, 24 -
Галерея Кейсов На Выставке Web-Studio 2009
19 Oct, 24 -
Uncharted 2: Среди Воров
19 Oct, 24 -
Подкаст Mobile-Review.com 97 От 29 Сентября
19 Oct, 24


