Когда-то я уже писал довольно большую статья об использовании эвристики в программировании , но сегодня я хочу привести небольшой практический пример.
этим летом я плыл на корабле по маршруту Москва – Ростов-на-Дону – Москва, и заметил, что каждый вечер директор круиза старается найти оптимальные места для туристических групп в автобусах.
Задача не такая уж и сложная, но на ее решение уходит не менее 15 минут в день.
Конечно, я пытался автоматизировать этот процесс.
Но, прежде чем описывать свое решение, необходимо точнее сформулировать задачу.
В самом начале круиза все туристы были распределены на несколько экскурсионных групп (в рассматриваемом случае их было 15), численностью не более 10 человек в каждой.
Все группы были пронумерованы по порядку, и полученный список групп не менялся до самого конца круиза.
Список выглядел примерно так: 
Каждый день туристы уведомляют директора круиза о том, на какие экскурсии планируют отправиться.
Из этого списка удаляются все, кто не планирует идти на основную экскурсию.
Именно с измененным списком нам предстоит работать.
Директор круиза подсчитывает, сколько человек собирается на экскурсию (обычно 100-120 человек), и делает соответствующий заказ на автобусы.
Турфирмы на берегу принимают этот заказ и предоставляют следующую информацию: «На пристани вас будут ждать три автобуса на 48, 48 и 50 мест».
В итоге задача оказывается следующей: необходимо рассадить туристов в автобусы, соблюдая следующие требования (в порядке важности): 1. Не разделяйте группы; 2. Заполнять автобусы максимально равномерно; 3. Желательно, чтобы группы, сидящие в одном автобусе, ехали подряд. Те.
первый автобус - группы 1-5, второй автобус 6-10 и т.д. Первый шаг к автоматизации был сделан с помощью Excel и надстройки «Поиск решения» (к моему удивлению, об этой настройке мало кто знает, хотя это невероятно полезная вещь).
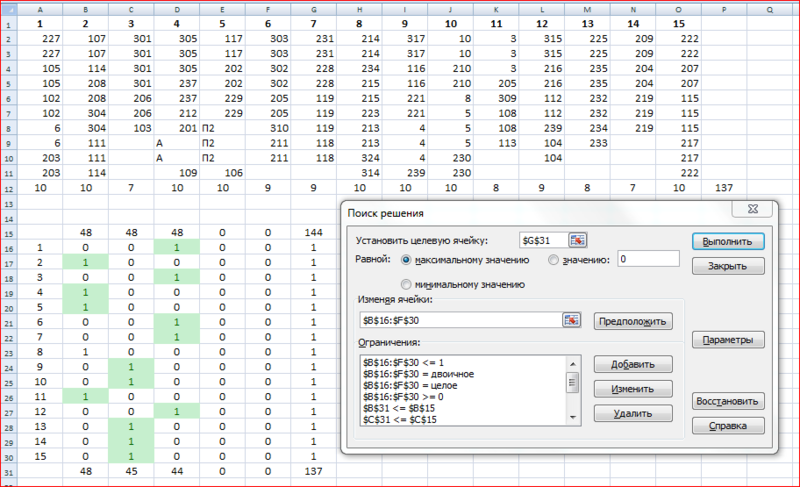
Первое требование, конечно, было выполнено, но о втором и третьем требованиях пришлось забыть.
Учитывая, что поиск решения на старом ноутбуке занимал около 15 секунд, было принято решение написать свой велосипед. Но тут снова возник вопрос: как все это сделать: симплекс-метод, динамическое программирование, метод ветвей и границ, эвристика? Наверняка есть какой-то сложный алгоритм, который поможет в решении этой задачи, но писать что-то сложное в отпуске и потом отлаживать это на ноутбуке с маленьким экраном? Я решил попробовать эвристику.
Немного подумав, я сразу же отложил подъем в гору, как и эвристику минимальных затрат и сбалансированной прибыли.
И тут я вспомнил об эвристике случайного поиска.
Честно говоря, я никогда раньше им не пользовался и был почти уверен, что случайный поиск не приведет к эффективному решению.
Но любопытство взяло надо мной верх.
В результате получился следующий алгоритм рассадки: 1. Выберите случайную группу и случайную шину.
2. Проверяем, можем ли мы посадить выбранную группу в выбранный автобус (смотрим, сидит ли эта группа в другом автобусе, и достаточно ли мест) 2.1. Если не можем, то увеличиваем счетчик неудачных попыток на единицу.
2.2. Если сможем, сбросим счетчик неудачных попыток.
3. Если количество неудачных попыток превысило 50, выходим из цикла, иначе переходим к шагу 1. 4. Проверьте, все ли группы расселись.
4.1. Если все верно, посчитайте максимальную разницу между количеством свободных мест в автобусах (это число будет считаться оценочным) 4.2. Если не все, сообщите о неудачной посадке.
Выполнив эту процедуру сотни раз, мы сможем выбрать расположение сидений с лучшим рейтингом.
Этот алгоритм работал на удивление хорошо.
По крайней мере, и первый, и второй пункт требований были выполнены на отлично.
Для выполнения третьего пункта необходимо внести небольшое изменение в алгоритм.
Еще до начала алгоритма рассадки мы поместим в каждый автобус по 5 групп (1-5,6-10,11-15) и осуществим рассадку.
В случае успеха мы запоминаем лучшую оценку и отображаем результат. Затем пробуем посадить в каждый автобус по 4 группы (1-4, 5-8,.
) и снова занимаемся рассадкой.
Если полученная оценка окажется лучше, чем на предыдущем этапе, мы запоминаем ее и выводим результат еще раз.
Затем мы пытаемся сначала посадить в автобус группы по 3 человека, группы по 2 человека, группы по 1 человек и, наконец, проводим процедуру рассадки без какой-либо предварительной информации.
Если на каком-то этапе оценка улучшилась, выводится полученное решение.
Конечно, действий выполняется больше, но ценность полученных результатов гораздо выше.
Напоследок небольшой пример работы программы: 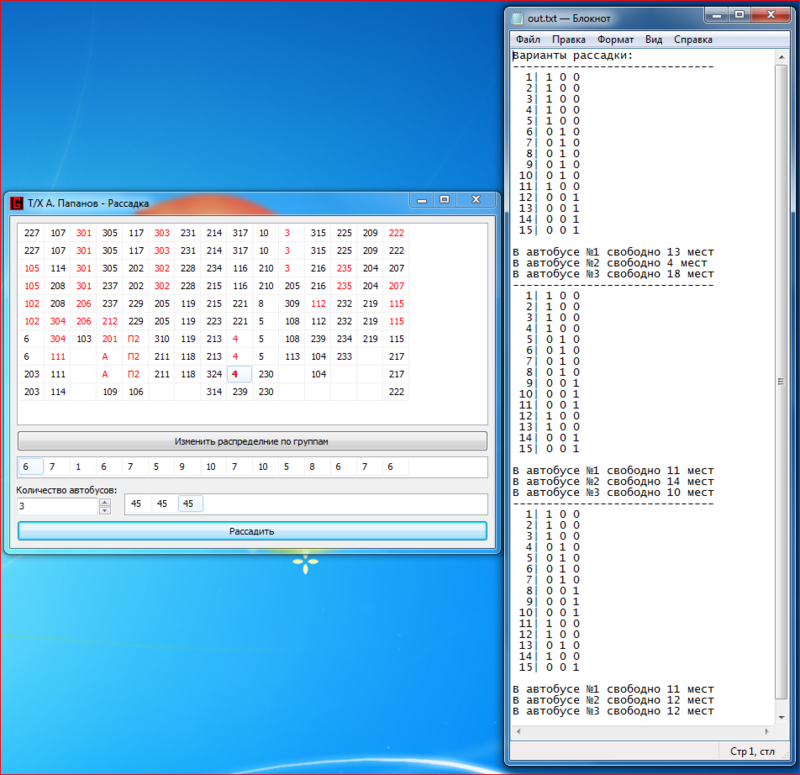
Понятно, что большинство из вас уже знают об эвристике случайного поиска, но вдруг этот пост прочитали люди, которые о ней не знают или по каким-то причинам боялись ее использовать.
Надеюсь, теперь, когда вы знаете эту эвристику немного лучше, вы сможете хотя бы немного облегчить решение некоторых своих проблем.
Теги: #эвристика случайного поиска #эвристика #алгоритм #Алгоритмы

-
Флеш-Накопители И Почему Они Так Хороши!
19 Oct, 24 -
Сервисы Для Совместных Покупок В Рунете
19 Oct, 24 -
Выигрышная Стратегия Гомоку – 35 Ходов
19 Oct, 24 -
Диалоги В Мобильных Играх
19 Oct, 24


