Электромагнетизм Для Самых Маленьких И Не Только

Если говорить об «электромагнетизме Максвелла», то люди в целом делятся на две группы: первые считают, что знают если не все, то вполне достаточно по этой теме.

Потому что ничего сложного там нет. Последние не совсем знают эту тему и знать не хотят. Так как формулы непонятны вообще.

Встречая в разных местах, как объясняются некоторые моменты: с одной стороны убедительно, с другой сомнительно, с третьей неверно, с четвертой в принципе верно.

Думаю, стоит присмотреться на них, на всякий случай, а поскольку начинать придется с основ, то даже «самые маленькие» смогут подняться, не опасаясь формул.

Прежде всего нас будет интересовать, как формируются и распространяются электромагнитные волны от «электрических» и «магнитных» полей, а потому сразу лакмусовая бумажка: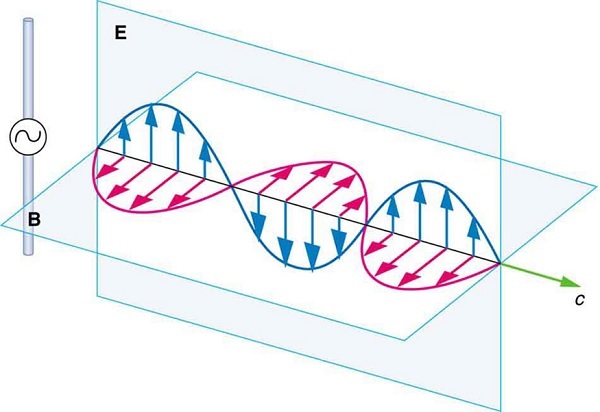

Электромагнетизм для самых маленьких и не только

Если эта схема вам очень знакома и не вызывает рефлекса, объясните и добавьте что-нибудь к ней, чтобы не вводить других в заблуждение, то прошу под кат. Если вам это очень знакомо, и вы понимаете, что требует дополнительных пояснений, то идите дальше) Пост не для вас.

Если схема не очень знакома и понятна, можно посмотреть.

Чтобы идти по порядку, начнем издалека, а именно возьмем и рассмотрим круг .

Казалось бы, здесь не о чем говорить; фигура не может быть проще.

С детства мы привыкли рисовать, беря на бумаге центральную точку и обрисовывая все точки, находящиеся на одинаковом расстоянии от центра.

Затем мы научимся другим способам «нарисовать» круг.

Казалось бы, это совершенно разные принципы, но они ведут к одному и тому же.

Возьмем один из них, один из самых полезных на мой взгляд: Тайна Вселенной

Электромагнетизм для самых маленьких и не только

Что это было? Не что иное, как дифференциальное уравнение окружности.

Смысл которого звучит так: «Есть две взаимодействующие сущности.

Первое применяет силу для усиления второго.

Второй, в меру своих возможностей, пытается ослабить первый».

Эту динамику мы можем записать в виде простейшей дифференциальной системы.

уравнения мира (не считая показателей степени)

Электромагнетизм для самых маленьких и не только

Образно говоря, в любой момент очень короткого периода одной и той же длины «dt» изменение «y» (т.е.

«dy») зависит от значения «x».

При этом в тот же момент изменение «x» (т. е.

«dx») зависит от значения «y».

Оба уравнения аналогичны уравнению макромеханики – «расстояние = скорость * время».

Только в этом случае отрезки «дт» очень малы (вернее, бесконечно малы, но суть от этого не меняется).

примечание о записи Обычно разница.

ур.

написано для демонстрации дифференциала, в данном случае производной по времени, поэтому типичным обозначением является: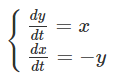

Электромагнетизм для самых маленьких и не только

При этом все эти зависимости линейны и о круге они ничего не знают. А принцип инь-ян проявляется в противоположных признаках влияния одной стихии на другую.

Если система не находится в равновесии, т.е.

«х» и «у» не равны нулю, то это взаимодействие, суммируя все микроотрезки времени, приведет к бесконечному циклу колебаний.

Пример HTML-кода

   

 <html>
 <body>
   <canvas height='300' width='300' id='cnv' style="border: 1px solid black"></canvas>
   <canvas height='300' width='200' id='cnv2' style="border: 1px solid black"></canvas>
   <script>
         var cnv = document.getElementById("cnv");
         var cx = cnv.getContext('2d');
         var cnv2 = document.getElementById("cnv2");
         var cx2 = cnv2.getContext('2d');
         var h = parseInt(cnv.getAttribute("height"));
         var w = parseInt(cnv.getAttribute("width"));
         var h2 = parseInt(cnv2.getAttribute("height"));
         var w2 = parseInt(cnv2.getAttribute("width"));
         var id = cx.createImageData(w, h);
         var id2 = cx2.createImageData(w2, h);
         var rd = Math.round;
        
         var x = 0, y = 1, x1, y1;
         var dt = 0.0001;
         var t=0;
         i=1000000; while (i--) {

Теги: #Популярная наука #физика #электромагнитное излучение #электромагнитные поля