Далее мы поговорим о том, как реализовать метод Screen Space Ambient Occlusion для расчета рассеянного освещения на языке программирования C++ с использованием API DirectX11. Рассмотрим формулу расчета цвета пикселя на экране при использовании, например, параллельного источника света:
LitColor = Окружающий + Рассеянный + ЗеркальныйИли, более формально говоря, сумма рассеянного, поглощенного и зеркального освещения.
Каждый из них рассчитывается следующим образом:
(цвет материала) * (исходный цвет) * (коэффициент интенсивности)Долгое время в интерактивных графических приложениях коэффициент интенсивности окружающего освещения был постоянным, но теперь мы можем рассчитать его в реальном времени.
Я хотел бы поговорить об одном из таких методов — Ambient occlusion, а точнее о его оптимизации — Ambient occlusion экранного пространства.
Давайте сначала поговорим о методе Ambient Occlusion. Суть его в следующем: для каждой вершины сцены сформировать некий коэффициент, который будет определять степень «видимости» остальной части сцены.

Рис.
1 – рисунок с комнатой и двумя точками, «видимость» каждой точки изображается в виде сферы Итак, для каждой вершины мы направим лучи в случайных направлениях и найдем их пересечение с геометрией сцены.
Далее мы посчитаем длину получившейся линии (если пересечения не обнаружено, будем считать, что луч имеет некую максимальную длину для данной сцены) и сравним ее с пороговым значением.
Если длина превышает пороговое значение, то луч проходит проверку видимости.
Количество пройденных испытаний, разделенное на количество выпущенных лучей, и будет коэффициентом видимости.
Очевидно, что высокая вычислительная сложность алгоритма делает его неприменимым в реальном времени или для сцен с высокой динамикой объектов.
Также эффективность метода сильно зависит от полигональной сложности сцены.
Этот подход разумно использовать, когда есть возможность заранее рассчитать «видимость» и сохранить ее как часть данных вершин или в текстуре.
К счастью, ребята из CryTeck (по крайней мере, я слышал, что они были первыми) придумали способ расчета шансов в реальном времени.
Это называется Screen Space Ambient Occlusion. Мой алгоритм реализации следующий:
- 1. Мы берем NDC (нормализованные координаты устройства) или координаты текстуры пикселей и преобразуем их в точку в пространстве камеры, используя данные о глубине;
- 2. Из этой точки мы стреляем N лучами в случайных направлениях;
- 3. Для каждого из N лучей:
- 3-а.
умножаем (масштабируем) наш луч (вектор) на определенное число (скаляр) и добавляем его к точке из шага 1;
- 3-б.
Преобразуем полученную точку в пространство NDC, а затем в текстурные координаты;
- 3-в.
Из текстуры мы получаем значение глубины для этой точки;
- 3-е.
Если полученное значение меньше глубины точки, полученной на шаге 3-а, то имеет место «перекрытие» (см.
рис.
2).
Необходимо учитывать, что эти значения принадлежат одной системе координат;
- 3-ф.
Коэффициент «перекрытия» получаем на основе зависимости «Чем дальше точка от точки 3-а находится от точки от точки 1, тем потенциально меньше возможное перекрытие от этой точки».
Давайте аккумулируем его стоимость.
- 3-а.
- 4. Получаем общий коэффициент «перекрытия», который равен сумме суммарного перекрытия/N лучей.
Поскольку общий коэффициент принадлежит [0,1], а видимость обратно пропорциональна перекрытию, то он равен 1 – перекрытие.

Рис.
2 – вектор нормали показан синим цветом, вектор, полученный на шаге 3-а, показан красным.
Светло-зеленый вектор — это направление оси Z. Если значение глубины в точке А больше, чем в точке Б, это перекрытие.
Для наглядности на рисунке использована ортогональная проекция (поэтому линия АВ прямая) Применяя этот алгоритм в пиксельном шейдере, мы можем получить данные о видимости, если запишем результат рендеринга в текстуру.
Данные из этой текстуры в дальнейшем можно использовать при расчете освещения сцены.
Итак, начнем.
1. Преобразования
Чтобы получить экранные координаты из трехмерных координат, нам необходимо выполнить ряд матричных преобразований.В целом таких преобразований три:
- 1. От локальных координат к мировым координатам - конвертируйте все объекты в общую систему координат.
- 2. От мировых координат до координат просмотра — ориентируйте все объекты относительно «камеры»
- 3. От координат вида к координатам проекции — проецируйте вершины объектов на плоскость.
Мы используем перспективную проекцию, которая включает в себя так называемое гомогенное деление — деление компонентов x и y вершины на ее глубину — компонент z.
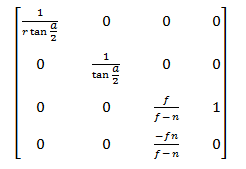
После умножения на эту матрицу координаты из пространства камеры переходят в пространство проекции
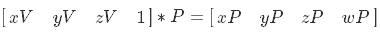
Далее следует однородное деление, в результате которого мы переходим в пространство NDC.

Теперь посмотрим, как сделать обратное преобразование.
Очевидно, сначала нам нужны координаты пикселей в шейдере.
Я считаю, что удобнее всего использовать квадрат, охватывающий всю площадь экрана в пространстве NDC, с текстурными координатами от (0,0) до (1,1).
Вот данные вершин:
Также необходимо установить точечную интерполяцию данных текстуры, например D3D11_FILTER_MIN_MAG_MIP_POINT. При рисовании этого квадрата мы можем либо «переслать» данные вершин в пиксельный шейдер следующим образом:struct ScreenQuadVertex { D3DXVECTOR3 pos = {0.0f, 0.0f, 0.0f}; D3DXVECTOR2 tc = {0.0f, 0.0f}; ScreenQuadVertex(){} ScreenQuadVertex(const D3DXVECTOR3 &Pos, const D3DXVECTOR2 &Tc) : pos(Pos), tc(Tc){} }; std::vector<ScreenQuadVertex> vertices = { {{-1.0f, -1.0f, 0.0f}, {0.0f, 1.0f}}, {{-1.0f, 1.0f, 0.0f}, {0.0f, 0.0f}}, {{ 1.0f, 1.0f, 0.0f}, {1.0f, 0.0f}}, {{ 1.0f, -1.0f, 0.0f}, {1.0f, 1.0f}}, };
VOut output;
output.posN = float4(input.posN, 1.0f);
output.tex = input.tex;
output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);Или непосредственно в пиксельном шейдере преобразуйте интерполированные координаты текстуры в пространство NDC следующим образом (подробнее об этом преобразовании см.
главу 3): float4 posN;
posN.x = (Input.tex.x * 2.0f) - 1.0f;
posN.y = (Input.tex.y * -2.0f) + 1.0f;
У нас есть координаты пикселей в пространстве NDC — теперь нам нужно перейти к просмотру пространства.
По свойствам матриц: 
Для наших целей нам нужна матрица обратной проекции.
Это выглядит так: 
Но нам недостаточно просто умножить на нее двумерную точку в NDC-пространстве и выполнить однородное деление — нам необходимо еще иметь данные о глубине точки, которую мы трансформируем.
Я хочу использовать глубину в пространстве просмотра — давайте проделаем несколько алгебраических преобразований и посмотрим, возможно ли это.
Сначала выразим переход точки из пространства обзора в пространство NDC: 
Теперь умножим на матрицу обратной проекции: 
Затем упрощаем X и Y и расширяем скобки в W: 
Далее продолжим упрощение в W: 
И последний штрих — уменьшить 1/n: 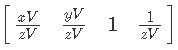
Получается, что после умножения на матрицу обратной проекции нам нужно умножить результат на глубину в пространстве обзора.
Вот что мы сделаем.
Сначала подготовим данные в пространстве NDC в вершинном шейдере: output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);
Затем займемся основной работой в пиксельном шейдере: float4 normalDepthData = normalDepthTex.Sample(normalDepthSampler, input.tex);
float3 viewRay = mul(input.eyeRayN, invProj).
xyz;
viewRay *= normalDepthData.w;
У нас есть координаты в пространстве обзора.
Вперед, продолжать.
2. Трассировка лучей
2.1 Данные смещения Итак, у нас есть координаты обрабатываемого пикселя в пространстве просмотра.Далее из точки с этими координатами нам нужно запустить N лучей в случайных направлениях.
К сожалению, в HLSL API нет инструмента, с помощью которого мы могли бы получить случайное или псевдослучайное значение во время выполнения шейдера независимо от внешних данных (или я просто не знаю о существовании таких технологий) — поэтому будем подготовьте такие данные заранее.
Чтобы получить их в шейдере, проще всего использовать текстуру.
Очевидно, что его «вес» и предел значений данных зависят от формата пикселя.
Для наших целей вполне подойдет формат DXGI_FORMAT_R8G8B8A8_UNORM. Теперь посмотрим на размер.
Наверное, самый простой, наглядный и в то же время неоптимальный способ — создать текстуру длиной и шириной, равными разрешению экрана.
В данном случае мы просто выбираем данные по значению текстурных координат квадрата, которые, напомню, находятся в диапазоне от (0,0) до (1,1).
Но что произойдет, если мы выйдем за эти пределы? Затем вступают в силу правила, указанные в перечислении D3D11_TEXTURE_ADDRESS_MODE. В данном случае нас интересует значение D3D11_TEXTURE_ADDRESS_MIRROR. Результат применения этого правила адресации показан на рис.
3. 
Рис.
3 - пример использования D3D11_TEXTURE_ADDRESS_MIRROR" Если мы воспользуемся этим подходом, то для наших целей различия будут приемлемыми (см.
рис.
4).

Рис.
4 - примитив с наложением текстуры 256х256 и с координатами от 0 до 1 и примитив с наложением текстуры 4х4 с координатами от 0 до 64 и адресацией D3D11_TEXTURE_ADDRESS_MIRROR Теперь, наконец, давайте заполним текстуру данными.
В шейдере мы сформируем вектор случайного направления из компонентов R, G и B тексела, поэтому мы не используем альфа-канал (можно представить его как компонент W, который равен нулю для векторов в однородное пространство).
В результате код выглядит примерно так: for(int y = 0; y < texHeight; y++){
Теги: #directx11 #ssao #ssao #C++ #Разработка игр #api

-
Почему Erp Для Бизнеса?
19 Oct, 24 -
Уйгурский Язык
19 Oct, 24 -
Виджеты Для Сторонних Сайтов
19 Oct, 24 -
Новый Пароль По Умолчанию В Sap
19 Oct, 24 -
Сборник Требований К Psd Макету Сайта
19 Oct, 24


