Странное устройство, известное как «оптическая машина Изинга», может контролировать воздушное движение и помогать НФЛ планировать игры.

В прошлом году сбой в системе распределения работы American Airlines мог привести к сбоям в расписании.
тысяч рейсов во время курортного сезона.
Эта ошибка позволяла пилотам отказываться от полетов без необходимости замены их другим пилотом, что подвергало риску около 15 000 полетов.
И хотя авиакомпании удалось вовремя отследить проблему и распределять сотрудников , этот беспорядок стал напоминанием о том, насколько мы зависим от компьютеров в организации расписания огромного количества сервисов и функций, от которых теперь полностью зависит наше сообщество.
Например, все крупные авиакомпании имеют сложные алгоритмы оптимизации расписания, которые подбирают пилотов к рейсам.
И хотя инцидент с American Airlines не произошел напрямую по вине алгоритма, исход мог быть аналогичным.
Подобный отказ оставил бы сотни тысяч людей в затруднительном положении или в очень неудобном положении, пока авиакомпания искала бы решение.
Триумф алгоритмической науки и закона Мура заключается в том, что теперь мы можем решать множество сложных задач оптимизации, включая такие области, как транспорт, логистика и планирование.
Большая часть современного мира не сможет нормально функционировать без этих алгоритмов: каждый год 50 000 грузовых судов транспортировать товары, произведенные 25 000 ТВтч электричество, а роутеры проводят через себя 1 Зеттабайт трафика .
Все это будет работать гораздо менее эффективно.
Однако организации часто работают с неоптимальными решениями из-за сжатых сроков и нехватки доступных компьютерных ресурсов.
Более того, еще есть много возможностей для улучшения методов, которые мы используем для решения большинства задач оптимизации.
Учитывая важность оптимизации и эпоху стабильных и значительных улучшений в скорости процессоров, похоже, подходит к концу, исследователи начали изучать, могут ли машины, специально разработанные для оптимизации, значительно улучшить нашу способность решать сложные проблемы.
Одним из перспективных подходов является разработка оптических машин, предназначенных для оптимизации.
Группа учёных из Стэнфордского университета (в которую входит автор статьи) под руководством Ёсихики Ямамото начала это исследование семь лет назад. Сейчас эту тему изучают несколько групп ученых, а также исследователи лабораторий.
После многих лет работы растет уверенность в том, что по крайней мере одна из этих групп однажды сможет создать машину, которая поможет нам подойти к некоторым из наиболее сложных задач оптимизации, которые требует решения современная промышленность.
Задача коммивояжера.
Сложность таких задач, как поиск кратчайшего пути между несколькими точками, увеличивается с увеличением количества точек.
Моделирование их как задач оптимизации Изинга может помочь решить их быстрее.
Вспомните классическую задачу о коммивояжере, в которой коммивояжер переезжает из города в город, продавая товары.
Он не хочет тратить время и деньги на бензин.
Это оптимизационная задача, цель которой — найти кратчайший путь коммивояжера, учитывая, что в каждую точку ему нужно добраться один раз, а в конце поездки он хочет вернуться туда, откуда начал.
Для пяти городов проблема решается просто.
Его можно рассчитать, просто рассмотрев все 12 способов .
Однако если трудолюбивый продавец намеревается посетить 50 городов, то метод перебора, рассматривающий все возможные пути, будет подавляющим — этих путей будет больше, чем Новемдециллион , или 10 60 - единица и 60 нулей.
Возможные решения такой проблемы могут быть даны нам с помощью алгоритмов, использующих разные пути обхода и разумные приближения.
Но даже лучшие из них способны заставить думать самый мощный компьютер.
В недавнем примере Университет Ватерлоо в Канаде попытался найти кратчайший путь среди почти 50 000 городов США, внесенных в Национальный реестр исторических мест, и докажите, что вы приняли правильное решение.
Для этого он использовал 310 мощных процессоров, которые работали безостановочно в течение 9 месяцев.
Но оптимизация включает в себя гораздо больше проблем, чем просто задача коммивояжера.
Еще одна трудная задача – планирование.
Например, Национальная футбольная лига США должна планировать несколько сотен игр каждый год, стараясь при этом соблюдать тысячи правил, которые, например, запрещают командам проводить более трёх игр подряд на выезде.
Для решения этой проблемы в 2017 году НФЛ использовала кластер 400 компьютеров .
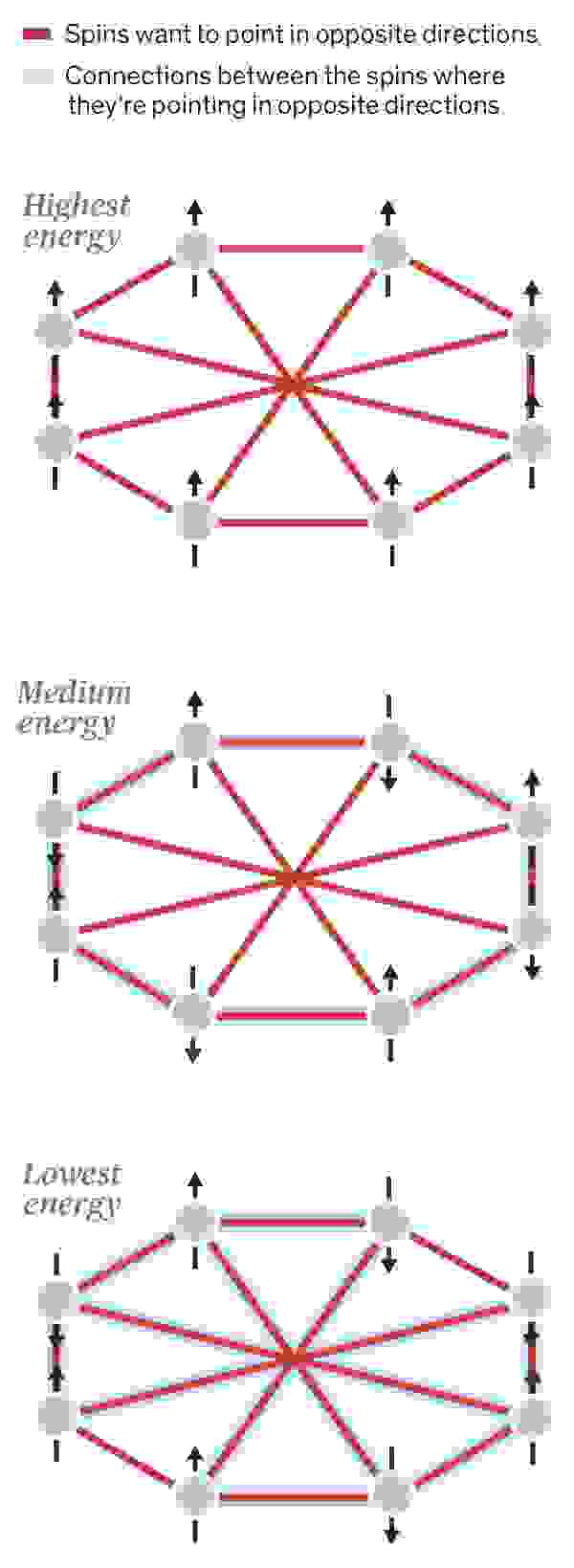
Оптимизация Изинга : В этой задаче Изинга энергия системы ниже, когда спины ее электронов направлены в направлениях, противоположных спинам ее соседей.
Системы, которые могут найти минимальное энергетическое состояние в модели Изинга, могут помочь ускорить решение сложных задач оптимизации.
Производственным предприятиям необходимо планировать техническое обслуживание оборудования.
Университетам необходимо планировать занятия.
Почтовым службам необходимо планировать маршруты доставки.
Крупные города, такие как Пекин или Токио, хотели бы научиться эффективно управлять потоком миллионов автомобилей, пытающихся проехать по их улицам в час пик.
Эти проблемы могут включать в себя сотни или тысячи мероприятий, которые необходимо спланировать, и во многих случаях практические решения все еще недоступны, поскольку требуют слишком много компьютерного времени или слишком большого количества компьютеров.
Исследователи уже много лет пытаются создать специальные машины для решения оптимизационных задач.
В середине 1980-х годов Дэвид Танк, работавший тогда в AT&T Bell Laboratories, и Джон Хопфилд, работавший тогда в AT&T Bell и Калифорнийском технологическом институте, предложили использовать аналоговые электронные схемы, представляющие собой нейронные сети, для решения задач оптимизации, таких как задача коммивояжера.
Их работа породила десятилетия исследований в этой области.
Затем, в 1994 году, Леонард Лэнгман из Университета Южной Калифорнии обнаружил, что теоретически ДНК можно использовать для решения подобных проблем.
Его идея вызвала аналогичный шквал исследований.
Однако эти попытки разработать радикально новые и эффективные подходы к решению задач оптимизации привели к появлению практических альтернатив обычным компьютерам и технологиям, которые сегодня остаются основными инструментами для решения таких задач.
Попытки создать специальные оптические машины, способные решать задачи оптимизации, сосредоточились на одной такой проблеме, известной как оптимизация Изинга.
Он был назван в честь физика Перста Изинга, известного своей работой над моделью магнитных моментов и объяснением переходов между различными магнитными состояниями.
Оказывается, многие распространенные проблемы оптимизации, включая планирование и поиск пути, можно легко преобразовать в задачи оптимизации Изинга.
Чтобы понять, как модель Изинга связана с оптимизацией, нам нужно начать с ее использования в физике для понимания магнетизма.
Рассмотрим обычный магнитный стержень.
Используя модель Изинга, можно представить магнитный стержень как трехмерную решетку атомов, в которой каждый из атомов сам по себе является магнитным стержнем.
Электроны в атомах обладают свойством, называемым спином.
Спины валентных электронов — находящихся во внешних оболочках атома — направлены либо вверх, либо вниз.
Направление спинов определяет намагниченность материала.
Если все спины направлены вверх, материал намагничен.
Если вниз, то материал тоже намагничивается – только с противоположной полярностью.
Если спины смешанные, материал не намагничивается.
Эти спины также взаимодействуют друг с другом.
В магнитном бруске» полная энергия " двух соседних электронов ниже, если их спины выровнены, то есть направлены в одном направлении.
И наоборот, их полная энергия выше, если спины направлены в разные стороны.

Оптическая машина Изинга.
Оптический параметрический генератор (ОПО) с обратной связью по измерениям может решать задачи оптимизации, выраженные в форме модели Изинга — набора спинов электронов и их влияния друг на друга.
Фазы оптических импульсов в OPO представляют собой спины, а влияние вводится в программируемую пользователем вентильную матрицу ( ПЛИС ).
Необходимо сделать около сотни проходов по системе, прежде чем импульсы в ОПО станут достаточно мощными, чтобы обеспечить решение проблемы.
В модели Изинга мы суммируем энергию взаимодействия между спинами каждой пары электронов в наборе атомов.
Поскольку количество энергии зависит от того, выровнены спины или нет, полная энергия набора зависит от направления всех спинов системы.
Таким образом, общая задача оптимизации Изинга состоит в том, чтобы определить, в каком состоянии должны находиться спины, чтобы минимизировать энергию системы.
В простейшей модели предполагается, что взаимодействуют только соседние спины.
Однако в общей задаче оптимизации Изинга любой спин может взаимодействовать с любым другим, независимо от расстояния, и знак и сила этих взаимодействий могут быть уникальными для каждой пары спинов.
В такой обобщенной постановке эту задачу решить очень сложно — так же, как решить задачу коммивояжера, посещающего сотни тысяч потенциальных покупателей.
Если мы сможем найти способ быстро решить проблемы оптимизации Изинга и способ думать о задаче коммивояжера и подобных проблемах так же, как и о задачах Изинга, мы, возможно, сможем быстро решить и эти проблемы.
Минимальная системная энергия в задаче Изинга будет представлять собой самый быстрый маршрут между городами, наиболее эффективное решение для упаковки грузового корабля или любую другую необходимую нам оптимизационную задачу.
Так как же превратить путь коммивояжера в вращения? Основная задача — сформулировать соответствие: нам необходимо представить нашу задачу оптимизации в том виде, в котором ее может решить машина, предназначенная для решения задач оптимизации Изинга.
Во-первых, вам нужно сопоставить исходную задачу оптимизации (скажем, поиск пути для продавца пылесосов) с набором вращений и определить, как вращения влияют друг на друга.
Благодаря исследованиям, проведенным за последние десятилетия как в области информатики, так и исследование операций , сравнение различных задач оптимизации с формами Изинга общеизвестный .
Однако с отдельными атомами и их электронными спинами сложно работать, поэтому мы сосредоточились на создании машины, которая реализует модель Изинга, используя импульсы света вместо электронных спинов.
Задача Изинга сравнивается с импульсами и взаимодействиями между ними.
Результат оценивается через полную энергию задачи, а оптимальным решением считается состояние с минимальной энергией.
Затем это решение переводится на язык, который имеет смысл для исходной задачи — например, кратчайший маршрут коммивояжера.
Ключом к способности нашего прототипа сопоставлять спины со световыми импульсами является OPO, устройство, похожее на лазер.
Но OPO, в отличие от обычного лазера, излучает свет, который находится точно в фазе или точно в противофазе с определенным базовым светом.
Это именно то, что необходимо для представления бинарных состояний вращения: вверх и вниз.
Мы можем думать о вращении вверх как о состоянии, в котором свет OPO находится в фазе с основным светом, и наоборот, вращение вниз соответствует свету, противоречащему фазе.
Существует несколько способов создания машины Изинга с использованием OPO. Группы из NTT, Калифорнийского технологического института, Корнелла и Колумбии, среди прочих, тестируют различные подходы.
Прототип машины Изинга, впервые продемонстрированный в Стэнфорде в ходе эксперимента под руководством Алирезы Маранди (сейчас в Калифорнийском технологическом институте), использовал технологию, с которой мы продолжаем работать: мультиплексированный OPO с временным разделением каналов и оптическим соединением.
Давайте разберем этот сложный термин.
Начнем с импульсного лазерного источника.
Источник посылает одновременные импульсы света длительностью несколько пикосекунд в двух направлениях.
Первый импульс становится базовым; он разделяется и идет по двум разным путям.
Второй используется как источник энергии для ОПО: он стимулирует кристалл в ОПО, который излучает импульсы фотонов.
Каждый импульс передается на катушку оптического контурного кабеля длиной несколько сотен метров, в зависимости от необходимого нам количества импульсов.
В этом кольце находятся сотни или даже тысячи импульсов ОПО, и они будут гоняться друг за другом по кругу, проходя через кристалл снова и снова.

Вверху: автор статьи и его бывший партнер по лаборатории Алиреза Маранди смотрят на прототип оптического компьютера Ising.
Внизу: большая часть действий происходит внутри катушки оптического кабеля.
Фазы этих импульсов будут играть роль спинов модели Изинга.
Но сразу после того, как они созданы, прежде чем пройти цикл несколько раз, они настолько слабы, что их фазы нечетко определены.
То, как мы заставим их взаимодействовать, в конечном итоге даст им финальную фазу и даст нам решение нашей проблемы Изинга.
Помните базовый свет из описания эксперимента? В одной точке контура имеется делитель, выделяющий небольшую часть каждого импульса, которая сравнивается с базовым импульсом в гомодинном детекторе.
Выходное напряжение детектора содержит информацию о фазе и амплитуде детектора.
Этот сигнал оцифровывается и подается на FPGA. Здесь и возникает сама проблема Изинга.
Напомним, что решение задачи Изинга означает нахождение минимального энергетического состояния для набора спинов, в котором спины взаимодействуют друг с другом по-разному, и эти взаимодействия добавляют дополнительную энергию к полной энергии системы.
В OPO каждый импульс представляет собой вращение.
Поэтому для каждого импульса — а в нашей установке мы использовали 100 — FPGA выполняет расчет, включающий записанные измерения всех остальных импульсов, которые, согласно задаче Изинга, должны влиять на рассматриваемый спин.
Затем процессор применяет расчеты к настройкам модулятора интенсивности и фазового модулятора, расположенных на одном из базовых путей прохождения импульсов.
Модифицированный базовый импульс подается в кольцо оптоволоконного кабеля, по которому дрожат импульсы ОПО.
Время имеет решающее значение: мы хотим, чтобы модифицированный базовый импульс сочетался с правильным импульсом OPO. Если все сделано правильно, два импульса смешаются.
В зависимости от того, находятся они в фазе или нет, импульс, введенный в систему, смещает импульс ОПО, чтобы представить вращение, направленное либо вверх, либо вниз.
Для каждого импульса ОПО в контуре мы повторяем весь этот процесс, и импульсы могут проходить десятки тысяч раз по всей длине контура, чтобы достичь конечных фазовых состояний.
Затем отдельный компьютер считывает набор фаз, интерпретирует их как электроны из задачи Изинга со спинами, направленными вверх или вниз, а затем превращает это в значимое решение исходной задачи оптимизации, которую вам нужно решить.
В наших экспериментах мы сначала создавали систему с четырьмя спинами, а затем с 16 спинами.
Параметры задачи были зашиты в установки в виде разветвлений оптического кабеля определенной длины.
В этих экспериментах мы успешно обнаружили состояния с минимальной энергией, и это дало нам мотивацию для развития этого подхода.
В 2016 году мы создали машину с замкнутым контуром на базе FPGA, способную решать задачи Изинга за 100 вращений.
Сравнение быстродействия нашей установки со специализированными системами, в том числе с аппаратом « квантовый отжиг » от НАСА, вселило в нас уверенность в том, что машины Ising OPO могут быть эффективными оптимизаторами.
Результаты многообещающие, но нам еще многое предстоит узнать, прежде чем мы узнаем, сможет ли этот оптический подход даже превзойти традиционный процессор в решении практических задач оптимизации.
Возможно, способность машины решать проблемы можно улучшить, используя квантовые состояния света, которые очень сложно моделировать.
Мы только начинаем решать многие из этих вопросов и планируем в течение следующих нескольких лет исследовать чрезвычайно интересное взаимодействие теории и эксперимента, разрабатывая этот новый тип вычислительной машины.
Теги: #математика #лазеры #физика #оптимизация #задача коммивояжера #модель Изинга

-
Издательство Питер. Черная Пятница 2017
19 Oct, 24 -
Полупрозрачный На Android И Настройка Resize
19 Oct, 24 -
Общение В Telegram Со Смартфонов Symbian
19 Oct, 24 -
Скрываем Rdp И Быстро Помогаем Пользователям
19 Oct, 24 -
Тестирование «Блондинка.ру»
19 Oct, 24


