Теорема о четырех цветах — это математическое утверждение, связанное с картами.
Все примеры карт, которые я нашел в Интернете, были слишком сложны, чтобы их можно было представить, поэтому я набросал свой неприглядный рисунок: 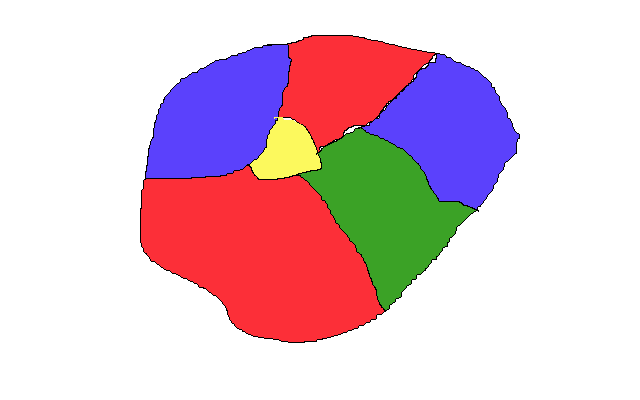
Если посмотреть на нее под другим углом, то можно воспринять ее как график — просто сожмите все области в круги и соедините круги, соответствующие соседним областям карты: 
Теорема о четырех цветах гласит, что для разметки любого рисунка, подобного моему (или соответствующего ему графика), достаточно четырех цветов, чтобы ни одна из соседних областей не имела одинакового цвета.
Это означает, что если мы возьмем карту Соединенных Штатов или Европы, даже со всеми этими причудливыми границами, и присвоим каждому штату или стране цвет, четырех цветов будет достаточно, чтобы разметить всю карту.
Некоторым картам нужны не все четыре цвета, а только два или три.
Карта, которую можно раскрасить в один цвет, будет не очень интересна, поэтому ее пропустим.
Первое, что поразило меня как разработчика ПО: четырех цветов недостаточно .
Кажется удивительным, что любой граф можно раскрасить только четырьмя цветами; Мне кажется, если бы я нарисовал графики некоторых кодовых баз, с которыми работал, где объекты, обменивающиеся данными, соединены ребрами, они запросто могли бы потребовать десяток цветов.
Итак, как вы догадались, в теореме о четырех цветах есть одно условие.
Должен быть счет плоский (плоский) .
Это означает, что никакие ребра не могут пересекаться.
Он должен иметь возможность перекрывать двумерную плоскость без пересечений.
То есть, если у нас есть граф с пересечениями, которые нельзя наложить на плоскость, то к нему не применима теорема о четырёх красках.
Для этого потребуется более четырех цветов, но чтобы нарисовать его без пересечений, потребуется как минимум три измерения.
Поэтому вы можете сделать это: 
но не так: 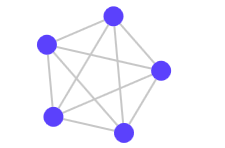
Сложность
Так что же интересного в этих цветах? Почему кто-то должен о них заботиться? Зачем я вообще пишу этот пост? Кратко это можно выразить одним словом - сложность .Количество цветов, необходимых для раскраски графика, указывает на его сложность: для более сложных графиков потребуется больше цветов.
Чтобы понять, как это будет выглядеть на практике, попробуем раскрасить графики.
Представленные ниже графики имеют одинаковое количество узлов, но для их раскраски требуется разное количество цветов (в оригинальной статье графы интерактивны и их можно раскрашивать, щелкая по узлам): 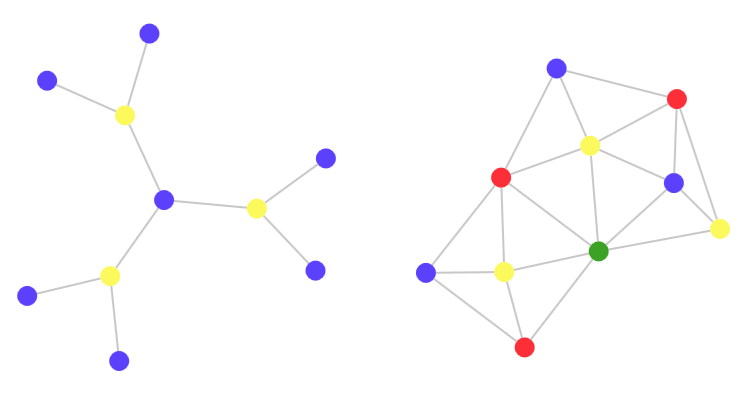
Второй график интуитивно кажется более сложным или, по крайней мере, менее упорядоченным.
Существует особый измеримый способ оценить его сложность: для его раскрашивания требуется больше цветов.
Для второго графа требуется четыре цвета, для первого — только два.
Почему? Сложность возникает из-за самой природы связей графа.
Некоторые компоненты второго графа сильно взаимосвязаны, в отличие от узлов первого.
Фактически, первый график создается на основе набора правил: это дерево .
Второй график был создан мной: я случайно щелкал мышкой, создавая множество связей.
Граф может содержать любое количество связей без увеличения количества цветов, если он упорядочен по определенным логическим правилам.
Количество узлов, подключенных к каждому узлу, не имеет значения: 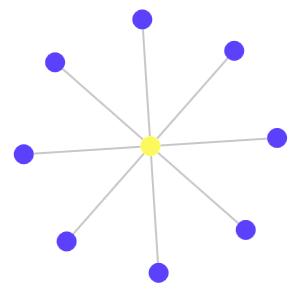
а также количество элементов в графе: 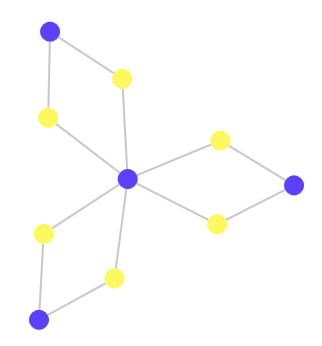
Фактически компоненты с большим количеством связей увеличивают количество цветов на графике.
В треугольнике мы получаем три цвета, но на самом деле треугольник очень взаимосвязан по количеству узлов: это полный график .
Интересная задача — переход от трех к четырем цветам.
Для этого необходимо добавить соединения между уже подключенными компонентами.
Допустим, мы хотим объединить следующие два графика: 
Есть способы сделать это без увеличения общей сложности и с ее увеличением.
Все зависит от того, как добавляются новые ребра: 
(Второй график нарисован с пересекающимся ребром, но на самом деле он плоский.
Если в исходной статье потянуть нижние узлы вверх, это будет исправлено.
) В первом графике я использовал узел 3 подключиться ко второму графику; узел 3 является как бы «интерфейсом» алмаза, ограничивающим доступ к нему.
Следуя этому шаблону, сложность графа не увеличивается.
Во втором графе узлы 1 , 2 И 4 иметь связи с более крупным подграфом.
В этом случае не существует единого узла, ограничивающего доступ к ромбу; граф большего размера имеет возможность подключаться к нескольким узлам ромба.
Это привело к увеличению сложности всей системы.
Кроме того, сложность распространилась на большую часть системы: я не могу изменить только один цвет узла, но должен распространить изменения на более крупный подграф.
Разработка программного обеспечения
Эти графики аналогичны графу зависимостей в базе кода.Если мы добавим узел для каждого класса и проведем ребра между классами, обменивающимися данными, в итоге получим граф, аналогичный представленному выше.
На мое упоминание терминов «компоненты» и «модули» повлиял тот факт, что я воспринимал эти графики с точки зрения программного обеспечения.
В последнем примере мы затрагиваем важную тему — вы можете управлять растущей кодовой базой, не увеличивая ее сложность, если управляете тем, как модули соединяются друг с другом.
Кодовая база, состоящая из небольших взаимосвязанных модулей, которые взаимодействуют четко определенным образом, будет менее сложной, чем та, в которой модули взаимодействуют случайным образом.
Это пример того, как лучше управлять взаимодействиями по точке, а не по ребру.
Я имею в виду, что модули, имеющие единую точку взаимодействия, смогут поддерживать свою собственную динамику, не усложняя кодовую базу.
Если программисты не думают о том, как они соединяют модули в кодовой базе, а полученные модули имеют несколько точек взаимодействия, то сложность кодовой базы возрастет. С точки зрения цветового измерения сложности деревья очень просты.
Для их окраски требуется всего два цвета.
Древовидная структура предотвращает создание взаимосвязанных кластеров, что приводит к резкому увеличению сложности, поскольку родительские узлы ограничивают доступ к дочерним узлам.
На диаграмме зависимостей родительские узлы представляют собой абстракцию поверх функциональности, предоставляемой дочерними узлами.
Если бы другие узлы подключались напрямую к дочерним узлам, абстракция была бы нарушена.
Однако большинство диаграмм зависимостей не являются деревьями из-за повторного использования кода.
Программист хочет, чтобы один объект использовался многими другими объектами.
Но только до определенного момента — нам не нужно, чтобы веб-представление напрямую взаимодействовало с уровнем хранения данных: во-первых, веб-слой находится на отдельном уровне абстракции, а во-вторых, у веб-слоя, скорее всего, будут другие обязанности, поэтому, когда при непосредственном общении с уровнем хранения данных в одном месте будет происходить слишком много всего.
Главный вывод из этих мыслей для меня заключался в том, что хороший способ управлять сложностью кодовой базы — использовать объекты, которые создают API поверх множества других.
Сложность графа никогда не увеличивается, если мы создаем соединения, соединяясь с точкой, ограничивающей внутренний граф.
Но если открыть «внутренности» наружу, можно быстро прийти к очень сложным графикам.
Теги: #теорема о четырёх цветах #кодовая база #управление зависимостями #программирование #управление разработкой

-
Google Научился Сравнивать Сайты
19 Oct, 24 -
Карикатурный Взгляд На Работу В Ит
19 Oct, 24 -
Консоль Vim В Windows
19 Oct, 24


