В следующем посте была интересная проблема, состояние которой следующее: Вероятность того, что в один из двенадцати стульев будут вшиты бриллианты, равна 0,9. Предположим, что стулья открываются один за другим, а к следующему переходят только в том случае, если на текущем стуле нет бубнов, найти вероятность того, что бубны окажутся на 12-м стуле.
На ближайшее время абстрагируемся от точных числовых значений и положим вероятность того, что ромбы пришиты, равной p, а количество стульев – n. Хотите узнать правильное решение этой проблемы? Добро пожаловать коту! Итак, начнем издалека.
Прежде всего, найдем вероятность того, что на первом стуле окажется бубна.
Используя формулу полной вероятности.
мы нашли 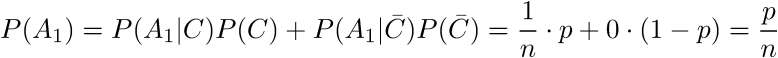
Поскольку мы проверяем стулья не одновременно, а по порядку, второй стул мы откроем только в том случае, если в первом ничего нет: 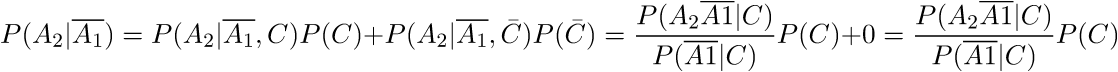
Здесь существует большой соблазн выявить числитель полученной дроби, используя правило произведения вероятностей, но этого делать не следует. Мы проверяем стулья по одному, а это значит, что наши мероприятия не являются независимыми.
Поскольку ромбы, если бы они были помещены, с равной вероятностью могли бы оказаться на любом из двенадцати стульев, вероятность события будет равна: 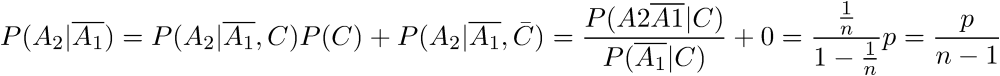
Выполняя новую итерацию, мы получаем: 
Опять же, события в знаменателе не являются независимыми, и мы не можем использовать формулу произведения вероятностей, но можем использовать формулу сложения вероятностей: 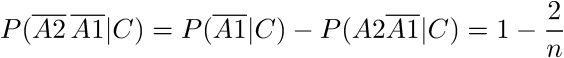
В результате получаем формулу: 
Теперь легко увидеть, что окончательная формула вероятности того, что на k-м стуле будет пришит ромб, выглядит так: 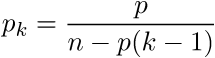
Подставим исходные значения: p=0,9 и n=12. В результате получаем ответ: 0.(428571) или 42,85%.
Особую благодарность хотелось бы выразить пользователю mayorovp, который заметил ошибку в расчетах, которую я допустил по невнимательности.
От всей души хочу пожелать, чтобы на его пути встречались только самые светлые люди.
С уважением, ProPupil. Теги: #вероятность #вероятность #вероятность #парадокс Монти Холла #Алгоритмы #математика
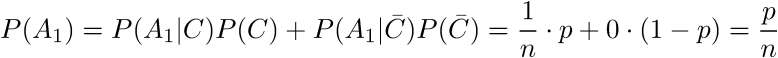
-
Украсьте Экран Своего Компьютера 3D-Обоями
19 Oct, 24 -
Дресс-Код Для Аватаров Введут К 2013 Году
19 Oct, 24 -
"Знаешь Что?" Или Stackoverflow Наоборот
19 Oct, 24


