Методы Ньютона-Котеса представляет собой набор методов приближенного интегрирования, основанных на:
разделение отрезка интеграции на равные интервалы; аппроксимация подынтегральной функции на выбранных интервалах полиномами; нахождение общей площади получившихся криволинейных трапеций.В этой статье будут рассмотрены несколько методов Ньютона-Котеса: трапециевидный метод; метод Симпсона; Метод Ромберга.
Трапециевидный метод
Метод трапеций – самый простой из рассмотренных.
В качестве примера возьмем следующий интеграл:
Точность аппроксимации зависит от количества N отрезков, на которые разбивается интервал интегрирования.
Таким образом, длина промежутка равна:
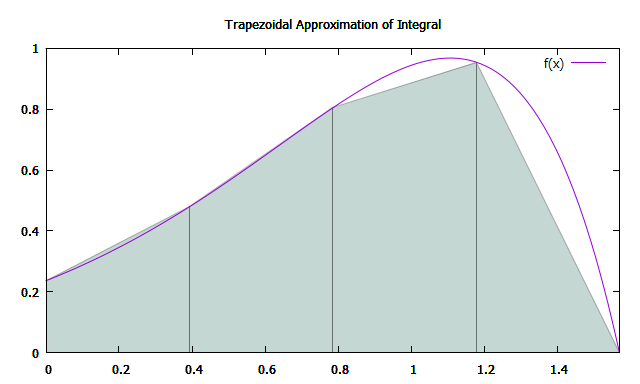
Площадь трапеции можно рассчитать по формуле:
Суммируя все вышесказанное, приблизительное значение интеграла вычисляется по формуле:
Функция, вычисляющая интеграл методом трапеций, должна принимать 4 параметра: границы интеграционного сегмента;
субинтегральная функция;
количество N интервалов разделения.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (b-a)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
Метод Симпсона
Метод Симпсона заключается в интегрировании интерполяционного полинома второй степени функции f(x) с узлами интерполяции a, b и m = (a+b)/2 - параболы p(x).Для повышения точности имеет смысл разбить отрезок интегрирования на N равных интервалов (по аналогии с методом трапеций), на каждом из которых применить метод Симпсона.
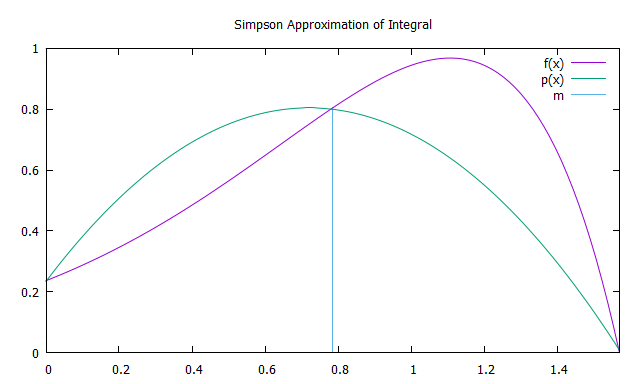
Площадь параболы можно найти, суммируя площади 6 прямоугольников одинаковой ширины.
Высота первого из них должна быть равна f(a), третьего-пятого - f(m), шестого - f(m).
Таким образом, находим аппроксимацию методом Симпсона по формуле:
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) {
const double width = (b-a)/n;
double simpson_integral = 0;
for(int step = 0; step < n; step++) {
const double x1 = a + step*width;
const double x2 = a + (step+1)*width;
simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2));
}
return simpson_integral;
}
метод Ромберга
Пусть T(x) — аппроксимация интеграла, полученного методом трапеций с шагом x. Получаем 3 таких приближения, уменьшая размер шага в 2 раза для каждого расчета.
Построим теперь параболу, симметричную относительно оси y, проходящую через точки T(1) и T(1/2), чтобы экстраполировать полученные значения для x, стремящегося к 0. 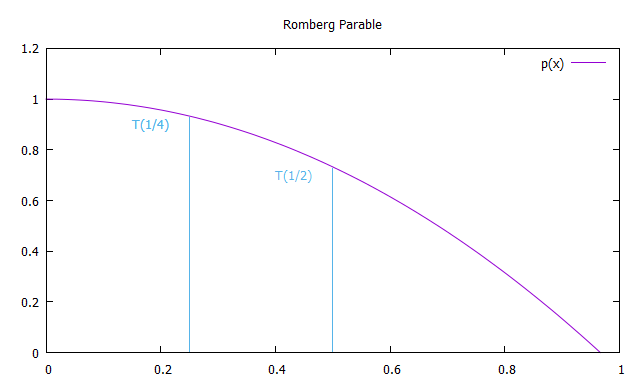
Следовательно, каждое слагаемое первого столбца R(n, 0) аппроксимации Ромберга эквивалентно решению, полученному методом трапеций, а каждое решение второго столбца R(n, 1) эквивалентно методу Симпсона.
Таким образом, формулы приближенного интегрирования методом Ромберга имеют вид:
Реализация на С++: std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) {
std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n));
romberg_integral.front().
front() = trapezoidalIntegral(a, b, 1, f); double h = b-a; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].
front() = 0.5*romberg_integral[step - 1].
front() + trapezoidal_integration*h;
for(size_t rbStep = 1; rbStep <= step; rbStep++) {
const double k = pow(4, rbStep);
romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1);
}
}
return romberg_integral;
}
Теги: #математика #C++ #математика
-
Почему Стоит Выбрать Наряд
19 Oct, 24 -
Почему Горят Дата-Центры
19 Oct, 24


