Яндекс существует уже некоторое время.
развивается беспилотный автомобиль.
Вот одна из первых технических лекций на эту тему.
Сотрудники «Яндекса» в разных городах, в том числе в Минске, работают над беспилотными автомобилями.
Автор лекции Роман Удовиченко родом из Минска — возглавляет группу обработки дорожной ситуации.
На сентябрьском субботнике Роман рассказал об одной из больших задач, стоящих перед его группой.
Мы просто берем текущее положение автомобиля, смотрим на путь, по которому нам хотелось бы идти, и плавно сворачиваем на этот путь и выруливаем на него.— Меня зовут Рома Удовиченко, я работаю в Яндексе в Минске руководителем группы обработки дорожной ситуации по направлению беспилотного транспорта.Оказывается, довольно просто.
Но передвижение по городу требует соблюдения правил дорожного движения.
Сегодня я расскажу вам об очень маленькой, но важной части нашей работы — алгоритмах построения траектории беспилотного автомобиля.
Для начала хочу понять, что нужно сделать, чтобы научить машину ездить самостоятельно - при условии, что мы ее обвешали датчиками, повесили камеры, радары и что там еще.
Мы можем все, все, что нам нужно сделать, это написать некоторый код предположений.
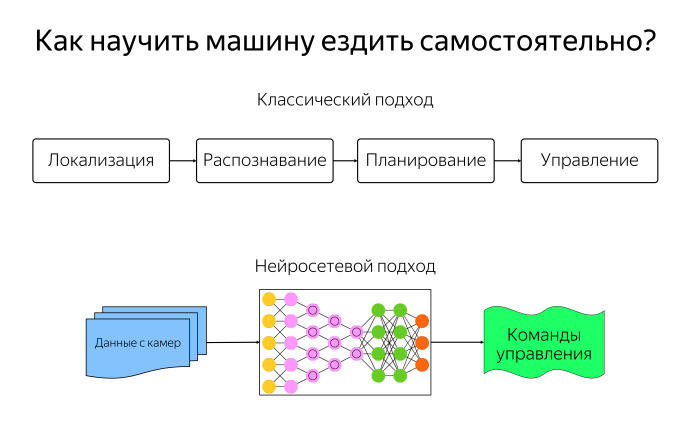
Мы можем использовать классический подход из робототехники.
Разделим нашу задачу самостоятельного передвижения на четыре модуля.
Модуль локализации отвечает за то, чтобы машина понимала, где она находится.
Модуль распознавания предназначен для того, что находится вокруг автомобиля.
Модуль планирования имеет информацию о том, что происходит вокруг, и зная, куда вы хотите отправиться, строит маршрут. Модуль управления подсказывает, как ехать по маршруту, чтобы приехать и завершить эту траекторию.
Или мы можем воспользоваться модной сейчас технологией нейронных сетей и сказать, что не будем ничего программировать явно.
Давайте просто скормим изображение с камер в нейросеть, предварительно обучив ее некоторым движениям человека.
Мы научим вас, в каких ситуациях нужно крутить руль, тормозить, газовать, брать много данных, делать большую нейросеть, и по задумке она после этого должна вести себя хорошо.
В этом направлении ведется большая работа, но на практике кажется, что нужно слишком много данных, нужна слишком большая нейросеть, чтобы успешно повторять все за человеком в различных ситуациях.
Поэтому сегодня мы поговорим о классическом подходе, в частности о планировании пути, построении траектории, по которой мы будем путешествовать.
Почему планирование маршрута — сложная задача, которую нельзя сделать за неделю, а потом пойти заняться чем-то интересным? Автомобиль вообще имеет ряд довольно существенных ограничений.
Это не шар в космосе, который может катиться в любую сторону и условно мгновенно останавливаться и замедляться.
У машины есть текущее направление, угол поворота колес, и она не может оказаться на два метра левее своего текущего местоположения, это очень сложно.
Он может двигаться примерно вперед, поворачиваясь под некоторым углом, но тем не менее движение весьма ограничено.
А траектория, которую мы строим, подвержена ограничениям, вытекающим из кинематики.
Например, мы не можем мгновенно ускориться или даже мгновенно увеличить ускорение.

Сегодня мы рассмотрим следующие виды алгоритмов построения пути, по которому сможет хорошо передвигаться автомобиль.
В частности, более-менее классические алгоритмы на графах, методы оптимизации, использующие непрерывные математические оптимизации, стохастические алгоритмы, учитывающие случайное поведение, и специализированные методы, которые решают очень специфическую задачу, но решают ее очень хорошо — лучше, чем в общем случае.
Первое, с чего мы начнем, — это графовые алгоритмы.
Первый вопрос, на который нам нужно ответить, чтобы понять, какие алгоритмы можно применять: как вообще построить граф? Вот машина, мы можем понять где она, но на самом деле графа нет, вершины ребер на дороге не нарисованы.
Нам нужно как-то самим придумать этот график.
Первое, что мы можем сделать, это: давайте разделим всё пространство на ячейки, посмотрим на маленькие ячейки и скажем, что вся наша поверхность земли разбита на ячейки 25 на 25 или 50 на 50 см.
Затем мы соединим ребрами соседние ячейки и будем искать по ним путь.
Это будет довольно далеко от расстояния, которое может проехать машина, но даст некоторое приближение.
И такие вершины у нас будут в двумерном пространстве.
Мы можем усложнить наше пространство, добавив туда текущий угол поворота автомобиля.
У нас уже будут ячейки не только x и y, но и текущая ориентация автомобиля по направлениям север, юг, запад и восток, тоже как-то дискретизированные.
Помимо направления мы можем учитывать много чего: текущую скорость автомобиля, текущее ускорение, текущее тангенциальное ускорение, нормальное.
Все это важно учитывать.
Но чем больше мы усложняем наше пространство, тем сложнее становится наш график.
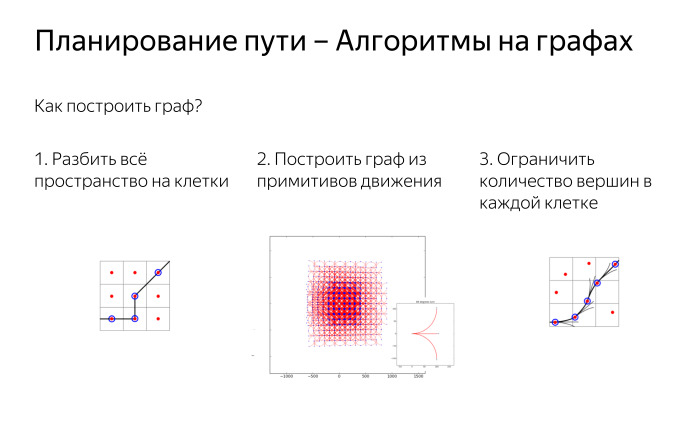
Помимо разделения пространства на ячейки, можно сказать, что мы умеем двигаться небольшими шагами в виде примитивов.
Например, проехать 50 см вперед или проехать 50 см вперед и повернуть налево, или проехать 50 см вперед и повернуть направо.
И такими примитивами мы можем вымостить всё наше пространство.
У нас нет ячеек в явном виде, но если эти маленькие шаги достаточно хорошо скоординированы друг с другом, то мы получаем регулярную сетку, которая хорошо и аккуратно покрывает пространство.
Предположим, мы рассматриваем примитивы, которые не так хорошо сочетаются друг с другом — например, скажем, поворот налево происходит под углом 89 градусов, а поворот направо — под углом 90 градусов.
Тогда у нас будет такое же количество вершин, как и на предыдущей картинке, которое будет занимать значительно меньшую площадь пространства, так как они плохо прилегают друг к другу и плотность точек будет очень велика, и мы не будем способный покрыть пространство далеко.
Мы можем объединить эти два подхода и сказать, что мы смотрим на примитивы движения под любым углом, движемся вперед, движемся вперед и поворачиваемся на 10 градусов, 15 градусов, как угодно.
В этом случае мы всё равно будем делить пространство на ячейки и говорить, что в одной ячейке не может быть более 1, 2,.
,k вершин.
Когда мы рассматриваем следующую вершину графа с помощью некоторого алгоритма, мы говорим, что в ячейке есть новая вершина, и обрабатываем ее соответствующим образом.
Если позже окажется, что мы хотим попасть в указанную ячейку в другой вершине, то мы это рассматривать не будем.
Это лишает нас возможности построить какой-то более оптимальный маршрут, чем если бы мы использовали все вершины.
Но это позволяет существенно повысить скорость и эффективность работы.
У нас есть граф, мы хотим применить к нему какой-то алгоритм.
Существует алгоритм A*.

Существует алгоритм Дейкстры, который немного более известен, чем алгоритм A*, и который обходит все вершины графа по мере увеличения расстояния от начальной вершины.
Он выводит их из некоторой очереди с приоритетом в порядке увеличения расстояния.
На верхней картинке мы видим, что если стартовая розовая вершина находится в начале, то мы постепенно будем рассматривать все вершины на радиусе, увеличивающемся от начальной, и в итоге придем к вершине, которая и является нашей целью.
Для более эффективного поиска мы будем учитывать вершины не только за счет увеличения расстояния от начала, но и добавить к этому расстоянию некую эвристическую оценку того, сколько времени нам осталось дойти до конца.
Логика очень понятна: мы не просто говорим, что сейчас стоим в какой-то вершине и поэтому рассматриваем следующую вершину по очереди на некотором расстоянии от начала.
Также мы добавляем к этому параметру некоторую функцию, позволяющую оценивать более перспективные вершины, от которых до финиша, скорее всего, недалеко.
Мы не знаем, сколько времени на самом деле потребуется, чтобы добраться от каждой вершины до финиша, ведь если бы мы знали, нам не пришлось бы искать путь.
Но мы можем это как-то оценить и получить картину на нижнем рисунке.
Мы будем оценивать вершины, которые каким-то образом идут к нашей цели, и будем рассматривать значительно меньшее количество вершин, чем в алгоритме Дейкстры.
Об этом можно говорить много, но в целом идея в том, что для корректной работы алгоритма необходимо, чтобы наша эвристика, функция оценки расстояния до конечной вершины, никогда не превышала фактического расстояния, которое нам осталось путешествовать.
Только в этом случае гарантируется корректная работа алгоритма.

В качестве эвристических функций можно использовать различные подходы.
В этом и заключается сложность использования алгоритма А*.
Чем лучшую эвристику вы сможете выбрать, тем лучше она будет двигаться к цели, тем меньше вершин она будет рассматривать и тем быстрее она будет работать.
Самое простое, что мы можем сделать, — это считать расстояние до цели напрямую.
Очевидно, что мы не сможем приехать к конечной точке быстрее, чем если просто едем прямо к ней, как танк.
Более сложная и эффективная эвристика — это расстояние, учитывающее наши кинематические ограничения, но не учитывающее препятствия.
Предположим, в мире нет ничего, только мы и цель, но машина не может мгновенно двигаться влево или вправо, она едет по своим законам, согласно существующей физической модели автомобиля.
Поскольку препятствий нет, мы можем заранее рассчитать расстояние до цели из различных мест, в которых мы можем находиться, и использовать это как эвристическую функцию.
Мы можем поступить наоборот: сказать, что есть препятствие, но допустим, машина может двигаться вперед, назад, влево, вправо, как угодно, быстро ускоряться и быстро тормозить.
Давайте построим нашу дистанцию с учетом препятствий, которые мы видим.
Мы снова получаем оценку, которая ниже фактического расстояния, которое нам осталось пройти.
Наконец, из всех эвристик можно рассмотреть максимальную.
Поскольку каждый из них не превышает нашего фактического расстояния, максимальный из них также не будет превышать фактического расстояния и алгоритм будет работать хорошо.

Что мы получаем? Алгоритм А* позволяет найти известный оптимальный путь, который приведет нас к цели, минуя препятствия.
Но если у нас маломерное пространство, мы учитываем только x, y, ориентацию автомобиля и тот факт, что он не может ускоряться мгновенно, а значит, все эти ограничения будут учтены.
Если мы добавим в наш график большое количество параметров, он будет расположен в очень многомерном пространстве.
У нас будет 7-, 8-, 10-мерное пространство, мы успеем рассмотреть небольшие кусочки этого пространства и не сможем построить достаточно длинный маршрут из-за очень высокой вариативности параметров.
В некоторых ситуациях A* сложно использовать, но в других он работает вполне хорошо.
Второй вариант — методы оптимизации, основанные не на дискретном, а на более непрерывном подходе.


Постановка задачи может быть следующей: рассмотрим траекторию нашего положения во времени x и y в зависимости от времени t, то есть поймем, в какой точке мы хотим находиться в момент времени t. Мы можем определить касательный угол через арктангенс производных; можно сказать, что оптимальной траекторией в этом случае будет та, которая минимизирует функционал, представляющий собой прямой интеграл по времени от некоторой функции траектории.
Функция траектории здесь как-то наказывает нас за резкие повороты, резкие ускорения, нахождение вблизи препятствий и т. д. Тогда, если мы просуммируем все эти штрафы по нашей траектории, которую мы себе придумываем, и попытаемся минимизировать это с помощью стандартной математической устройство, не имеющее никакого отношения к автомобилям вообще и беспилотным автомобилям в частности, то решим задачу в некой общей форме.

Какие примеры штрафов можно рассмотреть? Например, мы можем сказать, что не хотим подъезжать близко к препятствиям, учтите это с некоторым весом, мы не хотим, чтобы наша скорость была намного выше или ниже той желаемой скорости, которую мы для себя определили.
Мы можем наказать себя за вторую производную — ускорение, потому что мы не хотим, чтобы машина рухнула на пол и внезапно затормозила.
Мы можем рассмотреть третью производную, которая является рывком, то есть мы также не хотим, чтобы ускорение менялось достаточно резко.
Кстати, именно от резкой смены ускорения у людей возникает укачивание во время вождения.
Если ускорение фиксированное и машина все время просто ускоряется, то, как показывают исследования, люди не заболевают укачиванием.
Вестибулярный аппарат человека улавливает и не всегда хорошо реагирует, если он либо ускоряется, либо замедляется.
Возможно, мы не хотим делать резкие повороты, ограничивая угол наклона.
И есть дополнительные ограничения, которые гласят, что машина физически не может разгоняться быстрее некоторого ускорения.
Если мы все каким-то образом учтем это, мы сможем решить задачу, используя алгоритм минимизации абстрактной функции, и получить определенный результат. Отдельно хотелось бы поговорить о вычислении расстояний, потому что в большинстве методов оптимизации очень любят работать с хорошо дифференцируемыми и гладкими функциями.
Тогда там все работает хорошо.
А наша машина — это объект довольно сложной формы, и препятствия, которые мы объезжаем, — это тоже объекты сложной формы.
Поэтому здесь необходимо сделать некоторое упрощение.
Например, можно сказать, что машина — это не что-то сложное, а просто пять кругов, которые ходят туда-сюда.

Это будет похоже на правду, хотя и не полностью, но хорошее приближение.
А по кругам очень легко вычислить расстояния до чего угодно и очень легко проверить круг на пересечения с другими геометрическими примитивами.
Если расстояние до центра меньше радиуса, значит пересечение есть, в остальном все в порядке.
Что нужно, чтобы расстояние менялось плавно? Наше евклидово расстояние до невыпуклых многоугольников не обладает нужными нам свойствами и плохо дифференцируется в тех местах, где возникает эта невыпуклость.
Поэтому мы можем построить такое псевдорасстояние по полю градиента до нашей ломаной; здесь он отмечен красным и представляет собой препятствие.
Мы можем довольно легко ввести поле расстояний от каждой точки до этой ломаной, которое направлено в сторону ломаной и обладает необходимыми свойствами дифференцируемости - даже если это не строго кратчайший путь.
Если мы все это сделаем, то сможем построить плавную, красивую и аккуратную траекторию.

Преимуществами таких методов мы считаем то, что получается хорошая траектория и непрерывное пространство управления.
По нему можно ездить, все ограничения в той или иной степени соблюдаются.
Но, к сожалению, большинство методов оптимизации, или даже почти все, так или иначе страдают от локальных минимумов, когда их попытки оптимизировать что-то застревают и не могут найти достаточно хорошее решение.
Очень трудно сформулировать все в виде математических дифференцируемых функций; это тоже не всегда работает. Однако выход есть.
Мы можем использовать алгоритмы, которые работают несколько хаотично, но позволяют достаточно быстро и удобно построить некоторый приблизительный маршрут. Например, мы будем строить наш граф, представляющий собой дерево, итеративно.
Сначала мы не будем ничего делить на ячейки, не будем строить никаких примитивов.
Мы просто возьмем симулятор нашей машины, который в целом сможет имитировать движение, максимально приближенное к тому, как машина едет в реальности.
И давайте возьмем отправную точку.
После этого мы итеративно выбираем случайную точку в пространстве.
И — найдем ближайший к нему узел в текущем построенном дереве.
Давайте построим край к этой точке, используя симуляцию движения в этом направлении.
Получается, что каждый раз мы выезжаем из нашего построенного дерева в случайном направлении и мы можем сделать вершины в этом дереве в пространстве любой размерности, то есть в каждой вершине мы учитываем текущее направление движения автомобиля, текущее скорость, ускорение и все важные для нас углы.
И потом, когда мы возьмем новую точку, мы возьмем еще и ближайшую к этой точке вершину.
С помощью какой-нибудь симуляции проедем, например, 5 метров в сторону этой точки.
Затем возьмем еще одну точку и поедем к ней.
Что это нам дает? Мы каждый раз исследуем пространство, но очень агрессивно.
Мы не ищем оптимальные способы обойти препятствие.
Мы просто идем в разные стороны, но каждый раз делаем это от самой исследованной части нашего космоса к той неизведанной стороне.

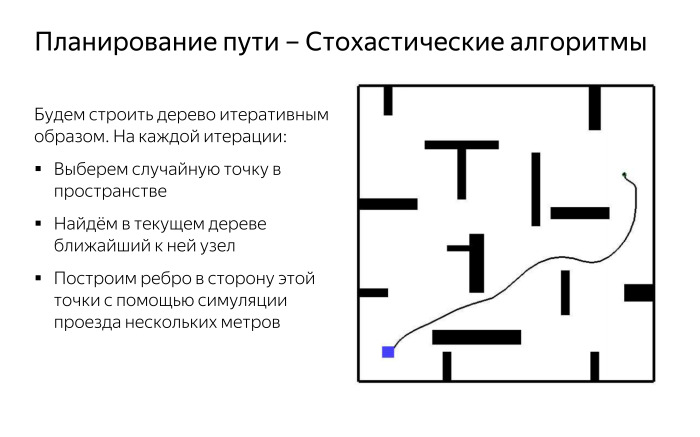
Благодаря этому мы довольно быстро получаем картину, где в разные стороны растут «щупальца», которые так или иначе охватывают наше пространство.
Возможно, не оптимально, но довольно быстро.
Квадрат в углу — наша исходная позиция.
Тогда мы сможем получить некий путь к цели, который может выглядеть не совсем оптимальным и элегантным, но получается достаточно быстрым способом.

И оказывается, что преимущества в том, что мы очень быстро работаем в многомерных пространствах.
Поскольку мы получаем пути с помощью честного моделирования, мы можем практически напрямую передать их в блок управления.
Недостатки? У нас нет гарантии, что наши баллы будут выбраны достаточно хорошо.
Решения могут быть достаточно кривыми и не всегда оптимальными.
Специализированные методы.
Когда машина едет по городу, у нас нет абстрактных точек А и Б и неструктурированной среды со случайными препятствиями.
В нашем городе все более-менее понятно: есть определенные полосы и движение нашей машины практически всегда заключается в том, что мы едем примерно по центру полосы, иногда смещаемся влево или вправо, чтобы объехать препятствие.
, иногда мы перестраиваемся, чтобы по правилам дорожного движения повернуть туда, куда нужно.
На перекрестках мы перестраиваемся с одной полосы на другую.

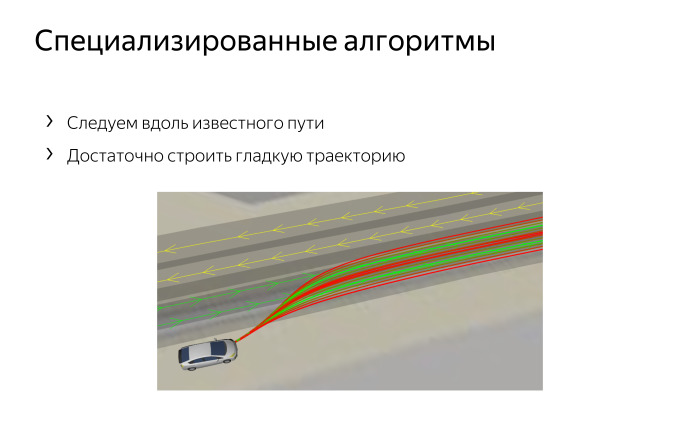
Нам не всегда нужны эти хитрые деревья, чтобы парковаться или выполнять сложные маневры.
Они нужны, но когда мы едем по полосе, нам достаточно построить более-менее плавную траекторию, следуя по центру этой полосы или с некоторым смещением влево и вправо.
Это гораздо проще сделать, чем искать абстрактный путь в графе.
Мы просто берем текущее положение автомобиля, смотрим на путь, по которому нам хотелось бы идти, и плавно сворачиваем на этот путь и выруливаем на него.
Оказывается, довольно просто.
Но передвижение по городу требует соблюдения правил дорожного движения.

Это не совсем связано с правилами построения пути, но недалеко от них.
Подъезжая к перекрестку, нам необходимо остановиться и пропустить движущиеся там автомобили.
Мы не можем ехать беспорядочно, мы можем ехать в ту или другую сторону, перестраиваться, должны останавливаться на красный свет светофора, пропускать пешеходов и т. д. И нам необходимо соблюдать правила дорожного движения, информацию о которых автомобиль может получить либо в заранее из какой-нибудь очень подробной карты, или узнавать ее на ходу по разметке, знакам и т.п.
И есть некоторая проблема с распознаванием всего этого на ходу.
Беспилотный автомобиль довольно легко поймать в ловушку.

Следуя правилам, он не сможет из нее выбраться.
Это шутка о том, как много в жизни случается ситуаций, в которых человек понимает, что ему делать.
Здесь сплошная полоса, впереди ремонт дороги.
Рабочие не установили все необходимые знаки объезда.
Они только что припарковали цементовоз и разбивают асфальт. Человек поймет, что ничего страшного от пересечения сплошной линии не произойдет — его, скорее всего, даже не оштрафуют. А вот с беспилотными автомобилями все сложнее.

В общем, в процессе решения возникает масса проблем дорожного строительства — во всех смежных областях, которые были вначале.
Если вы хотите помочь нам разобраться с этими сложностями и реализовать всё в алгоритмах, обязательно приходи к нам делать добро .
Будем рады видеть Вас в группе развития Минска.
Построение разных дорожек и учет правил дорожного движения — лишь одна из наших тем.
Большое спасибо.
Теги: #математика #Алгоритмы #маршрутизация #разработка робототехники #беспилотный транспорт #Промышленное программирование #графики #трафик #задачи оптимизации #геоданные #Минск #алгоритм а* #стохастическая оптимизация #оптимальный путь

-
Поддержание Связи Где Угодно
19 Oct, 24 -
Как Попасть В Темную Сеть?
19 Oct, 24 -
Сервис Backports Становится Официальным
19 Oct, 24 -
Бета-Версия Chrome 5.0 Для Mac Os X
19 Oct, 24 -
Настройки В Приложениях Android
19 Oct, 24


