Как сказано в определении, выпуклая оболочка какой-то набор 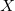
это наименьшее выпуклое множество 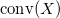
, содержащий набор 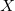
.
Выпуклая оболочка конечного множества попарно различных точек является многогранником.
Для реализации одномерного случая алгоритма Quickhull используется функция std::minmax_element .
В сети можно найти множество реализаций алгоритма Quickhull для плоского случая.
Однако для случая произвольной размерности на сайте сразу находится только одна тяжеловесная реализация.
В скобках рядом с терминами приведу переводы на английский язык (в стиле Tubo, извините).
Это может быть полезно для тех, кто еще не знаком с терминами и будет читать англоязычные тексты по ссылкам, или решит разобраться в текстах исходного кода.
Упомянутая выше «каноническая» реализация написана на C (есть привязки к C++), давно и широко используется (в составе пакетов GNU Octave и MATLAB) и, следовательно, хорошо протестирована.
Но если вы решите изолировать код, связанный только с одним алгоритмом Quickhull, вы столкнетесь с трудностями.
Для простых приложений хотелось бы обойтись чем-то более компактным.
Немного потрудившись, я написал собственную реализацию ( https://github.com/tomilov/quickhull ): Это один класс без каких-либо зависимостей.
Всего около 750 строк.
Геометрические понятия.
Когда начинаешь работать с многомерными объектами, понимаешь, что некоторые аналогии со знакомыми двух- и трехмерными объектами справедливы.
Необходимо несколько упорядочить знания: ввести некоторые новые термины и уточнить взаимосвязи между ними.
Для программиста геометрические объекты — это прежде всего структуры данных.
Для начала дам геометрические определения (не очень строгие).
Ниже по тексту мы приведем описания соответствующих структур данных, удобных для хранения данных и достаточно эффективной работы с ними.
Обозначим размерность пространства как 
.
- Симплекс определяется выражением
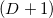
аффинно независимая точка.Об аффинной независимости я расскажу дальше.
Эти точки называются вершинами (англ.
unit vertex, множественное число vertices).
- Многогранник (син.
многогранник, многогранник, англ.
многогранник, многогранник) определяется как минимум
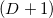
точка (вершина),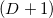
из которых должны быть аффинно независимыми; симплекс (англ.simplicial multitop) — простейший случай

-мерное тело: многогранники с меньшим количеством вершин обязательно будут иметь ноль
-мерный объем. - Параллелотоп – это обобщение плоского параллелограмма и объемного параллелепипеда.
Для симплекса можно построить
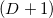
соответствующие параллелоэдры (все они будут иметь одинаковый объем, равный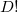
объемы симплекса), принимая в качестве образующих (векторов) параллелоэдра векторы, исходящие из одной фиксированной вершины в каждую из остальных
пики - Я не буду здесь давать понятие выпуклого многогранника (англ.
uvex multitope, uvex multihedron); ваше интуитивное представление об этом подойдет. Симплекс, рассматриваемый как частный случай многогранника, всегда выпуклый.
- Понятие плоскости изначально и неопределенно.
Обратите внимание, что его размерность на единицу меньше, чем пространство, в которое он встроен.
- Симплициальная фасет определена

аффинно независимые точки (вершины).Далее мы будем говорить только о симплициальных объектах (кроме выпуклого многогранника), поэтому определение понятия «симплициал» я опущу.
Многие последующие утверждения будут справедливы только для невырожденных (все точки попарно различны) случаев симплициальных геометрических объектов.
- Ребро определяется как пересечение двух граней и имеет
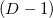
вершина.Две грани могут иметь только одно общее ребро.
Следовательно, одно лицо может иметь

соседи через ребра. - Пик (англ.
peak) определяется
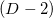
точки.Здесь может всплывать интуитивная аналогия с трехмерным пространством, поскольку понятия вершины и вершины не совпадают, но оперировать такими объектами мы не будем.
Грань может иметь любое количество соседних ребер по вершине, из чего можно сделать вывод, что хранение графа смежности ребер по вершинам затратно как в памяти, так и с точки зрения затрат на поддержание релевантности структур данных при любых преобразованиях.
.

В многомерном пространстве видимые или наблюдаемые объекты могут быть только
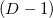
-мерные объекты, то есть границы

-мерные объекты.
Английский термин «фасет» — это именно наблюдаемая грань.
Прямая линия всегда является одномерным объектом.
В этой градации точку (вершину) можно считать нульмерной.
Работа с некоторым набором 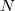
точки, мы можем перейти к рассмотрению соответствующего набора 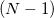
векторов путем вычитания одной из точек из всех остальных.
Таким образом, мы как бы присвоим эту точку началу координат. Если все точки лежат в одной плоскости, то плоскость смещается таким образом, что начинает проходить через начало координат. Аффинная независимость 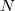
точки удовлетворяются, когда удовлетворяется линейная независимость 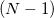
соответствующий вектор.
Вы наверняка уже знакомы с определением линейной независимости векторов.
Таким образом, в 
- в мерном пространстве больше выбрать нельзя 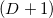
точек так, что все они аффинно независимы.
Поясню: в трехмерном пространстве треугольник (грань трехмерного симплекса — тетраэдра) определяется тремя точками (не лежащими на одной прямой, конечно); через эти три точки проходит одна плоскость; любая точка этой плоскости, добавленная к множеству трех вершин треугольника, превратит множество из трех аффинно независимых точек в множество из 4 аффинно зависимых.
Аналогия справедлива и для других измерений.
Помимо прочего, необходимо ввести понятие гиперобъема.
Гиперобъем.
Любой рассматриваемый предмет из серии симплекс , край , край , вершина горы и т. д. ограничены в соответствующем подпространстве.
«Объем пространства», который занимает такой объект, можно измерить/определить/задать.
Для одномерной линии мера называется длиной; для двумерной плоскости мера называется площадью; для трехмерного тела – объем.
Понятие можно обобщить, назвав его D-мерным объемом или D-гиперобъемом.
Для симплекса, образованного попарно различными точками 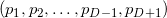
(порядок перечисления точек важен), гиперобъем можно вычислить Так : 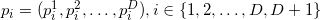

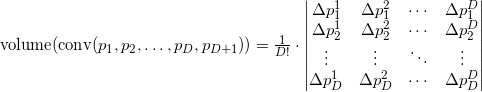
Здесь мы выписали координаты векторов строками.
Аналогичные формулы и рассуждения можно привести и для векторов-столбцов (т.е.
если мы транспонируем все матрицы, то на результат и выводы это не повлияет).
Детерминантный делитель в приведенной выше формуле — это количество симплексов (все они имеют одинаковый объем), на которые можно разбить параллелоэдр.
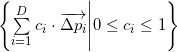
, построенный на векторах 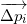
.
Соответственно, сам определитель является гиперобъемом параллелоэдра.
Тем, кто интересуется причинами этого утверждения, я рекомендую прочитать об определителе матрицы Грама и его геометрической интерпретации.
Следует отметить, что эта мера для «объемных» объектов будет иметь ненулевое значение, а также может быть как положительной, так и отрицательной.
Смысл знака нетрудно понять из следующих соображений: поменяв местами две точки симплекса, мы получим изменение знака определителя; порядок точек — это «левая и правая ориентация» симплекса.
На плоскости легко представить: если стороны треугольника 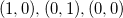
перечислено против часовой стрелки 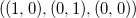
, то определитель положителен 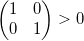
, в противном случае 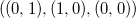
- отрицательный 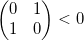
.
Для тетраэдра знак будет зависеть от того, в каком порядке (по часовой стрелке или против часовой стрелки) перечислены первые 3 точки, если смотреть на них со стороны последней.
Таким образом, в дальнейшем при указании геометрических объектов мы должны принять, что порядок перечисления точек должен быть фиксированным.
Множитель перед определителем можно опустить, так как алгоритм будет использовать только информацию о знаке значения ориентированного гиперобъема.
Определитель равен нулю, если хотя бы две строки линейно зависимы (помним, что точки попарно различны, то есть ни одна строка не равна нулю).
Легко проверить непротиворечивость приведенных выше рассуждений об аффинно зависимых точках и соответствующих им линейно зависимых векторах.
На абсолютное значение определителя не повлияет то, какую точку мы вычитаем при переходе к векторам — только знак.
Всегда следует вычитать последнюю точку из первых, иначе для одинаково ориентированных подобных объектов, используемых в дальнейшем, знак меры будет разным в четных и нечетных измерениях.
Что делать с мерой предметов, вложенных в пространство слишком большой размерности, например, с мерой лиц? Если построить матрицу так же, как показано выше, то она будет прямоугольной.
Из такой матрицы невозможно взять определитель.
Оказывается, формулу можно обобщить (это обобщение связано с Формула Бине-Коши ), используя ту же матрицу, состоящую из векторов-строок: 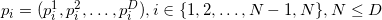
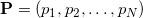
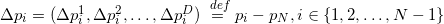
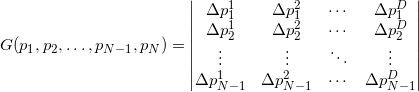
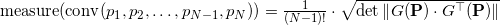
Для аффинно независимых попарно различных точек матрица под определителем всегда оказывается квадратно положительно определенной, а сам определитель такой матрицы всегда является положительным числом.
Для аффинно зависимых точек матрица будет сингулярной (т.е.
ее определитель равен нулю).
Понятно, что мера всегда неотрицательна и информации об ориентации у нас нет.
С одной стороны, определитель произведения квадратных матриц равен произведению определителей, с другой стороны, определитель транспонированной квадратной матрицы совпадает с определителем исходной, таким образом, последняя формула сводится к формула для 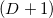
точек, за исключением квадратного корня, т.е.
модуля, который мы можем опустить, чтобы получить дополнительную информацию об взаимной ориентации точек в пространстве.
Алгоритм.
Сам алгоритм Quickhull для случая произвольной размерности был предложен в работе Барбер, К.
Брэдфорд; Добкин, Дэвид П.
; Хухданпаа, Ханну (1 декабря 1996 г.
).
«Алгоритм Quickhull для выпуклых оболочек».
Транзакции ACM в математическом программном обеспечении 22 (4): 469–483 .
«Каноническая» реализация на C от авторов находится на уже упомянутом сайте.
http://qhull.org/ , репозиторий с интерфейсом C++ https://gitorious.org/qhull/qhull .
Приведу алгоритм из первоисточника:
Теги: #quickhull #выпуклая оболочка #gnuplot #qhull #C++ #Алгоритмы #математика #Визуализация данныхcreate a simplex of d + 1 points for each facet F
-
Я Просто Хотел Android 1.5
19 Oct, 24


