Ээта статья продолжается обсуждение как более понятно объяснить алгоритм Косараджу — поиск сильно связных компонент в графе.
В статье дано изложение и обоснование корректности алгоритма.
Этот пост будет полезен студентам, изучающим графовые алгоритмы, а также тем, кто хочет улучшить/освежить свои знания в этой области.
Чтобы понять алгоритм Косараджу, необходимо знать некоторые понятия теории графов.
Базовые концепты
сильно связные вершины u, v Пики ты, в называются сильно связан , если в графе G существует путь (не обязательно прямой) и→в И в→у (Обозначим сильно связные вершины и↔в ), и для каждой вершины ты истинный ты ↔ ты

Компоненты сильной связи Компоненты сильной связи -- максимальные сильно связные подграфы Инвертировать граф -- изменение направления всех ребер в графе на противоположное (двунаправленное ребро остаётся самим собой) часы DFS от верхней в -- обойти ( в глубине ) все вершины графа, достижимые из в .
Тик можно интерпретировать как рекурсивный вызов функции.
Цикл обработки вершины, не имеющей соседей, будет равен 1. Максимальное время выхода -- число, соответствующее времени выхода рекурсии алгоритма DFS из вершины.
Более того, изначально счетчик времени равен 0; оно увеличивается только в двух случаях:
- Начало нового тика DFS
- Прохождение по ребру (неважно, рекурсивный это проход или нет)

Обойдем его с помощью алгоритма DFS, разметив вершины по правилам, указанным выше:

Мы обозначаем непройденные вершины знаком '?' Мы выберем начальную вершину в порядке возрастания непомеченных вершин.
Изначально счетчик 0 
Начинаем новый цикл с выбора вершины 0 (как вершины с минимальным индексом).
Увеличиваем счетчик на 1 и присваиваем это число метке вершины 0. Попутно мы построим деревья часов DFS справа от исходного графа.

У вершины 0 только один сосед — вершина 2. Идем по ребру 0-2, увеличивая счетчик и присваивая метку вершине 2. 
У узла 2 нет соседей.
Поэтому все, что мы можем сделать, это рекурсивно вернуться к предыдущей вершине (чтобы понять, какая вершина была предыдущей, мы строим дерево).
Идя по рекурсивному ребру 2-0, мы увеличиваем счетчик на 1 и присваиваем вершине 0 новую метку.

У вершины 0 больше нет непомеченных соседей — цикл завершается.
Начиная новый цикл, мы увеличиваем счетчик и присваиваем метку счетчика следующей (по возрастанию) вершине.
Также начинаем строить дерево нового такта.

У вершины 1 есть 2 соседа: 0 и 3. Но у вершины 0 уже есть метка — перейти к ней нельзя.
Затем идем в вершину 3, увеличивая счетчик и присваивая метку 
У вершины 5 нет непомеченных соседей.
Возвращаемся к предыдущей вершине, увеличивая счетчик и присваивая новую метку 
У вершины 1 больше нет соседей — цикл завершается.
Мы также видим, что все вершины отмечены.
Алгоритм поиска в глубину завершен Из примера видно, что вершина в начале такта (корень) имеет самую большую (в такте) метку - это объясняется рекурсивностью алгоритма DFS - алгоритм заходит в одну вершину и оставляет то же самое.
Этот факт понадобится в доказательстве.
Вот несколько простых лемм: Лемма 1 : Если правда ты ↔ в И в ↔ ш , тогда правда и↔в Доказательство : Поскольку и↔в , Что в достижим из ты , у нас также есть v↔w , Означает ш достижим из в .
Следовательно ш достижим из ты , сходным образом, ты достижим из ш .
Мы получаем и↔в Лемма 2 : Сильно связная компонента — это множество вершин, входящих в множество циклы, имеющие хотя бы одну общую вершину 
цикл A имеет общую вершину u с циклом B Доказательство : Заметим, что все вершины одного цикла входят в одну компоненту связности, так как по циклу из любой его вершины можно дойти до другой.
Если два цикла имеют общую точку, то через нее можно перейти к вершинам другого цикла и достичь любой из них.
Таким образом, все вершины, принадлежащие связным циклы между собой, включены в одну связную компоненту.
Рассмотрим любое из максимальных объединений циклов С .
Докажем, что вершина не включен в С , принадлежит другой сильно связной компоненте.
Докажем это от противного.
Пусть вершина v не входит в объединение циклов С , но сильно связан с одной из вершин этих циклы ты .
Тогда по определению сильной связи существует путь из вершины в до ты и путь от пики ты до в .
Склеив (конкатенацией) эти пути, мы получим цикл, связанный с объединением циклически проходит через вершину ты , но не входит в С , что противоречит предположению.
Обратите внимание, что эта лемма дает представление о том, как увидеть в графе сильно связные компоненты.
Лемма 3 : Инвертирование ребер цикла не влияет на его цикличность.
Доказательство : Если исходный граф имеет путь от ты В в , то инвертированный граф будет иметь путь из в В ты.
Алгоритм Косараджу
Алгоритм Косараджу предназначен для поиска сильно связанных компонентов в ориентированном графе и состоит из трех шагов:- Выполняйте поиск в глубину (DFS), пока все вершины не будут «помечены».
Вершина считается «помеченной», когда ей назначается время выхода из рекурсии (см.
основные понятия).
- Инвертировать исходный график
- Выполните DFS в порядке убывания меток вершин.
Прежде чем доказывать алгоритм, предлагаю посмотреть на примере, как работает алгоритм.
Пример пошаговой работы алгоритма Косараджу
Учитывая следующий график: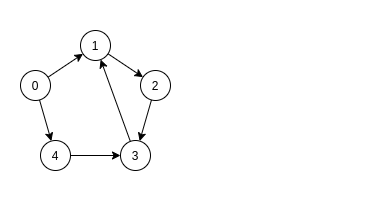

Шаг 1: Непомеченные вершины помечены знаком '?' Справа от исходного графика находится лес DFS. Начальная вершина выбирается в порядке возрастания индексов.
Полный протокол работы я не показывал, но он доступен в разделе «основные понятия».

Шаг 2: Инвертирование краев 
Шаг 3: Выбираем начальную вершину в порядке убывания меток.
Поскольку сейчас нас интересует только лес тактов DFS, то считать время выхода из вершин нет смысла, поэтому рекурсивные переходы я не показывал.
Справа от перевернутого графика показывает лес часов DFS 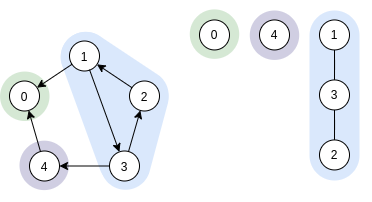
После завершения алгоритма у нас есть 3 сильно связных компонента.
Доказательство корректности алгоритма
Давайте немного уточним, что нужно доказать : Пики ты И в сильно связанный ⇔ после выполнения алгоритма они принадлежат одному и тому же дереву часов DFS. Доказательство : ⇒ Если вершины ты И в были сильно связны в графе G, то на третьем этапе будет найден путь от одной вершины к другой (по лемме 3), так как на первом шаге путь и → в, и на третьем - путь в→у.Это означает, что в конце алгоритма обе вершины лежат в одном дереве.
⇐ 
Пики ты И в лежат в одном и том же дереве поиска в глубину на третьем шаге алгоритма.
Это означает, что они оба доступны из корня р это дерево.
Вертекс р рассматривалась на шаге 3 раньше всех остальных, а значит время выхода из него на шаге 1 больше, чем время выхода из вершин ты И в .
Отсюда получаем 2 случая:
- Обе эти вершины были достижимы из р в исходном графике.
Это означает сильную связность вершин ты И р и сильная связность вершин в И р (согласно лемме 3).
Склеивая пути получаем связность вершин ты И в (по лемме 1)
- По крайней мере одна вершина не достижима из р в исходном графике, например в .
Это значит р не был доступен из в в исходном графике, поскольку время выхода р - больше (если это было достижимо, то время выхода в было бы больше, чем р, посмотрите еще раз на первый шаг примера).
Это означает, что пути между этими вершинами нет (ни в исходном, ни в инвертированном графе), а последний существовать не может, поскольку по условию в достижим из р на шаге 3 (в перевернутом графике)
Сложность алгоритма
Поиск в глубину в исходном графе выполняется за O(V+E) Чтобы инвертировать все ребра в графе, представленном в виде списка смежности, требуются действия O(V+E).Для матричного представления графика не требуется предпринимать никаких действий для его инвертирования (индексы столбцов будут использоваться в качестве индексов строк и наоборот) Количество ребер в инвертированном графе равно количеству ребер в исходном графе, поэтому поиск в глубину будет выполняться за O(V+E).
В результате получаем, что при нижней оценке Сложность алгоритма - O(V+E) Верхняя оценка (когда у нас полный граф) будет следующей (напомним, что количество ребер в полном графе равно н вершины равны п(п-1)/2 ):
То есть в худшем случае мы имеем квадратичная сложность
Нижняя граница
Алгоритм Косараджу ищет сильно связанные компоненты, и делает это за время в лучшем случае O(V+E), а в худшем — за O(V^2).Где применить алгоритм, полностью зависит от вашей фантазии по созданию графиков.
Например: проецирование транспортной сети на граф.
Алгоритм поможет проверить вновь созданную транспортную сеть на достижимость каждой вершины из каждой вершины (убедиться, что есть путь от окраины к центру и обратно).
Вы можете использовать алгоритм для проверки системы воздуховодов в зданиях; ток в полупроводниковых устройствах Можно мыслить шире: мы проектируем кровеносную систему живого существа, которую вам поручили создать в рамках проекта генной инженерии, где-то в 2077 году).
Алгоритм поможет узнать, доходит ли кровь до органов и обратно от сердца.
Теги: #Алгоритмы #Косарайю #сильно связанные компоненты

-
Требования К Графическому Дизайнеру
19 Oct, 24 -
Настоящее, Которое Определит Наше Будущее
19 Oct, 24 -
Три Вида Вечной Жизни
19 Oct, 24


